物理科学探疑——每周一文    第四期   2001年12月14日

动量守恒定律不能普遍成立

志勰

[简介]本文介绍了火箭燃料燃烧喷射过程、电荷变速运动间的作用、流体动力学中不遵守动量守恒定律的几个现象。火箭燃料燃烧喷射过程中获得的动力过程中修正了原文中的错误。

    目前，至少如下的三种情况，动量守恒定律不能成立。它们分别是火箭燃料燃烧喷射过程中获得的动力过程、电荷变速运动间的作用、流体动力学也不遵守动量守恒定律。下面分别来探讨：

一、火箭燃料燃烧喷射过获得的动力过程

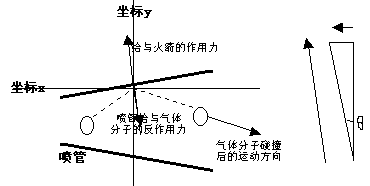
    通常认为，火箭的动力来自于火箭高温高压的燃气向下喷射时所获得的反冲力，这样的看法仅仅是火箭产生动力的形式看法。高温高压的燃气向下喷射时，火箭如何获得反冲力，采用牛顿第三运动定律却不能对此建立解释的途径。但是燃气分子是高速运动的气体分子，它和火箭燃烧室的作用只能是弹性碰撞。因此，火箭燃料燃烧喷射过程获得的动力，在计算方法上应该采用气体分子和燃烧室的弹性碰撞来获得。计算燃烧室和气体分子之间的弹性碰撞所构成的矢量作用力，即火箭所获得的动力。

    我们通常采用高温高压燃气喷出火箭喷管时的动量的积分来计算火箭获得的总动量的计算方法，是不对的。在火箭燃料燃烧向下喷射燃气获得动量的过程中，存在两种动量不守恒：一种不守恒来自于火箭燃烧室燃气的密度问题、另一种不守恒来自于燃气和火箭喷管间的作用。下面我们分别讨论。

    1、火箭燃烧室燃气的密度所形成的动量不守恒

    如果火箭单位时间燃烧的燃料是一个确定的常数，那么单位时间里产生的气体分子的数量也是一个确定的常数，同时，火箭单位时间所喷射出去的气体数量也等于这个确定的常数。不考虑火箭燃烧室的散热问题，这样，燃烧时内部气体的温度可以当作常数处理，即气体分子的运动速度为一个常数。火箭所获得的动力来自于气体分子和燃烧室的有效的产生矢量作用力的碰撞，这里简称有效碰撞。这个有效碰撞截面积等于火箭喷管的截面积。因此我们只需要计算火箭喷管截面积上单位时间内所获得的动力。为了便于说明问题，这里采用比较两个成比例的火箭喷管面积所受到的动量来说明，这里看作喷管收缩。如果火箭喷管截面积在收缩前后获得的动量相同，那么动量守恒定律成立，否则不成立。如图：

    这里为了便于简化分析过程，采用比较的方法。

    火箭喷管截面积收缩了n倍，那么收缩前后燃烧室内的气体密度相差n倍。采用常规的处理方法（理想气体状态方程），可以得到火箭喷管收缩前后，火箭动力没有变化。这里面没有处理的一个问题是气体分子的自由程，如果将这个问题考虑进去，那么可以得到火箭喷管收缩后的动量是收缩前喷管截面积所获得动量的倍。（这里请注意，原文中的密度和自由程关系是错误的，应该是密度三次方根的倒数等于自由程，而不是原文中的反比。可参见本站观点纠正）

    （在热力学的压强公式计算中，也没有考虑自由程这个问题，这里可以认为在理论上存在争议，但是处理的对象是不同的，一种是高温高压，另一种是普通气体。我想最好的方法就是采用实验验证）。

2、燃气和火箭喷管间的作用给与火箭整体的不守恒

火箭燃料的再次利用     如果火箭喷管仅是一个燃气的出口，那么火箭燃料燃烧所获得的动力为ft的话，那么右图中将火箭的喷管做成喇叭形的设计则在这个基础上提高一个增量，即ft+△ft。因为向后喷出的气体分子已经不具有使火箭向前运动的动力。但通过将火箭喷管做成喇叭形，可促使向后喷出的气体分子继续给与火箭向前运动的一个动力增量。燃气分子相对于火箭的运动速度则没有区别。仅仅是一个多次碰撞的问题。但这可以认为使火箭的整体不再遵守动量守恒定律。

二、电荷变速运动间的作用

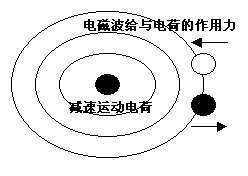图中的椭圆圈表示电磁波，黑白两个球表示正负两种电荷。     电磁波一旦产生，可以脱离发射体而独立的存在。带电粒子变速运动，可以产生电磁波。     当电荷相对于其它的电荷作减速运动时，它会对其它的电荷产生电磁波的作用。并且电磁波会对其它的电荷产生作用力，同样的一个电磁波列对正电荷和负电荷所产生的作用力的方向是相反的。

    依据动量守恒定律，一个物体沿某方向动量减少，那它必然在和其它物体相互作用时，使其它物体沿这一方向动量增加。在电磁理论中却不是这样了。针对于电磁波的发射电荷的动量变化，在它所产生的电磁波和其他电荷的相互作用中，我们通过电荷的属性的不同，总可以找到和发射体的动量变化是同样变化的一种电荷。这样动量守恒定律在电荷的变速运动过程中不再成立。

三、流体动力学中的动量不守恒现象

如图：在水流出小孔B之后，水由于水压的作用，得到了速值为v的状态。如果我们依据动量守恒定律，那么只要我们计算一下水流冲出小孔B获得的动量和水缸由于水流冲出小孔B所获得的冲量是否相等就可以了。     水流获得的动量我们可以对单位时间里流出小孔B的水量和速度的乘积就可以了。     水缸获得的冲量我们可以采用水压的方法进行计算。水缸在小孔的高度h1这一个圆环上由于小孔将放出，在小孔这个截面上压强减小，但水缸除此之外由于水的压力所形成的作用力不变，因此形成一个和小孔B水流反方向的由水压所形成的一个矢量作用力，只要我们将这个作用力和时间的乘积则得到水缸获得的冲量。

    我们需要计算一下单位时间里压力所形成的冲量，以及水流从B小孔冲出获得的动量的数值。

    计算表明：ft=ghSt和mv=2Sghtρ。

    不论我们两组数据如何取值，我们都不能得到两组数据是相等的结论。至此，动量守恒定律在流体力学中不能成立。

火箭燃料燃烧喷射过程中获得的动力过程的内容来自物体在介质中运动动力的原理——空气动力 、电荷变速运动间的作用的内容来自动量守恒定律不能在电磁理论中成立的简述 、流体动力学中的动量不守恒现象的内容来自流体动力学中的动量不守恒现象  。在火箭燃料燃烧喷射过程中获得的动力过程中修正了原文中的错误。详细的请参见本站观点纠正

作者电邮：zhixie@netease.com 返回首页