物理科学探疑-网友天空-系统观点-赵庄愚--宇宙复变函数结构论The
Theory of Cosmic Structure of the Complex Variable Functions（A）
宇宙复变函数结构论
The Theory of Cosmic Structure of the Complex Variable Functions
Zhao Zhuangyu
赵庄愚 (Jan.28,1911~ Jan.8,1991)
简介：时空关系历来被认为是实函数关系，这是一个误解，因而造成了物理学中一系列不能解答的迷思。本论由能量分析的启发和虚实律理的获得,而确认证明了时间与空间二者之相互关系有如复数，即有互虚的性质.我们可以论证: 凡宇宙时空组合的结构皆具有复数性质. 两者本身相对(时对时, 空对空) 而言, 也是复数的性质.
一切物理观测, 都是根据空间与时间的测定来进行的. 空间时间的组合就是宇宙的结构. 它们的相对关系有空间对时间, 空间对空间, 以及时间对时间三种. 本论在此初始阶段, 只略举三种之中的两三件代表性的例子来说明其通性, 而更深入的论证将留在<时间论> 和<空间论> 中进行阐述.
时间空间, 两个被人们实感着, 被哲学科学定为框架的东西, 其结构的性质怎样? 科学至今尚未明确地证明. 二者的体大无穷, 延长无穷, 精细度也无穷.科学依据它, 使用它的程度愈进入高深, 则它之所以成为谜反而亦趋更高深.若干不能解的问题更有增生, 究竟是甚么原因呢? 原来, 我们一直到今天只知道用实函数关系去看待它定义它之故. 经研究发现, 它不能是实函数的关系, 而是复函数性质的结构, 这是有证可举有理可阐明的.
本论由能量分析的启发和虚实律理的获得,而确认证明时间与空间二者之体属虚,
其相互关系有如复数. 即有互虚的性质. 我们可以论证:
凡宇宙时空组合的结构皆具有复数性质. 两者本身相对(时对时,
空对空) 而言, 也是复数
的性质. 下面, 我们将展开进一步的论述.
一切物理观测, 都是根据空间与时间的测定来进行的. 空间时间的组合就是宇宙的结构. 它们的相对关系有空间对时间, 空间对空间, 以及时间对时间三种. 本论在此初始阶段, 只略举三种之中的两三件代表性的例子来说明其通性, 而更深入的论证将留在<时间论> 和<空间论> 中进行阐述.
首先需要提到的是: 如果我们未能清楚地区别各种时-空组合的性质与关系,则不可能真正解开现代物理学中的许多旧题与新迷.重新考察时空,拟是今日物理的当务之急. 这篇研究仅作为最初始最简要的导论.
一. 论成为实在与不成为实在
科学的任务是求“实在”。然而，必须知道科学不可能避免讨论“虚在”。(“虚”也是一种“存在”, 即虚数, 虚量, 虚因子,… 等). 若避免讨论“虚”则不可能真正探求到“实”的本质. 惟有实地了解“虚”与“实” 的性质和变化,才能判别事物成为实在与不成为实在的区分,而后,方可探讨论证科学的真理.凡相对能够成为“实在”的根据, 不只是依靠对它作物理量度的假设,并且还要对其它的假设，中间的比较，和计算等，全部过程都取得实量而不含虚量， 才能具备成为“实在” 的的条件. 这当中必需具备的条件是:
1)
对象可以被实测，并且不受实测影响而发生变化。
2) 量度的结果可以相互比较，可相加减，可作推导。
3)仪表对所测的物体彼此可以划齐, 可以互相推衍.
4)间接量度的确实倚变性，可以划齐，可以互相推衍。
以上条件即说明在观测两事物关系时，须这两者具有可以互相量度，互相加减，彼此划齐，有确定的倚变关系，而且没有独立的或矛盾的两个假设条件，然后两者可被认为是具有相对成为“实在”的关系。可略举例如下：
1)相对论否认两地有同时性，即因于两地各之时间彼此只有互虚之关系：1。两地或两天体之计时仪表其可以划齐只是一种假设，无可以作实比。2。两地距离须给定，要确认其间无外场的影响，没有相对运动，是不能自证的，这仅又是一假设。3。“时间”需建立于能以直接比较，这又必需要添上“两地时间有等时性有彼此可相加减性”这个假设。而实际上彼此时间恰不可相赠予，不可相加减，此一假设显然不合实情。因此，凡认为两地同时的，除其距离很近，能肯定彼此之间无相对运动以及无场的影响者外，其结论都不会成为“实在”。它涉及两地时间不可以划齐，不具等时性；不能作加减，不可相赠予性；尤其假设又有多个，违反了成为“实在”的条件，所以说“两地同时”只具有“虚在”的性质。
2) 互相垂直的两个矢量(如力)有互虚性，互相垂直的力其物理量纲虽然相同，但彼此的数是不可以相加的。要用几何加法，其相对的分力都为零。不发生实数关系，要中间加入改变一个力之方向使不互垂直，然后，一个的分力可以和未变矢向的力相加。故相互垂直的两个矢量直接相加，都不能成为实在，而只有互为虚在的性质。
3)
无穷大对有限数是互为虚在的。因为无穷大不可以和有限数相加减相比较，不产生实数关系，故两者也是互为虚在的性质。
于是，凡不具备成为“实在”的诸条件者，其相对体即含有互为虚在的性质。一般认为其相对关系，只能具有复数及复变函数的关系。
二. 空间对时间的结构是属于实与虚的结构
空间时间的组合，是物理观测最基本的项目。可举速度，加速度，和作用三者来探讨其普遍性，更由天体运动，物体振动之时空关系以知其广阔性。
(1) 速度：
S: 空间距 t:
时间这是物理空间时间最简短的组合，最为基本的观测量。要考察其为实为虚，可以：
a)设S是定在刚体上的距离。不涉及坐标运动及外场关系，此
有可定之实。再看 
，这需附
于
点，附 
于 
点，就发生两地有无同时性及等时性的问题。要肯定其有同时性与等时性并无其成实的依据，(上述相对论之所否认)这就是又一假设，假设多于一个，中间即有虚性。
相对于
中含有虚，即t 为
复数S是实数。复除实只能得复数，此V值只能为复函数。
b)设
是定轨道上天体之运转周期，有可定之实。则其
非刚体上两
点之距离，有其复杂的场存在及有其对不同场心的不同距离变化。(如卫星对地球对太阳还有对其它天体之不同距离)此
S 相对于 t 又具有虚度。此之 V
值是实数除复数，仍是 复函数。
通常测地上相对静止两点间物之运动速度，其距离成实，其时间是因光速联通可以有近于实的“同时”，只此种所测得之V才可以接近纯实数，又测天体运动时，设行星对日只有两体运动关系，没有三体或多体的影响，其在各处的速度乃亦是实数而非复变数。超于此之外，V即带有虚数，一般为复变函数的性质。
可是以往在传统上，仅仅把V认识为属于相对的实数值，并没有把时间与空间理解为具有互虚及V是属于复变函数的关系。
(2) 加速度： 
, 
这里亦可假设如加速度是由引力场所产生，对场心之距离
是有定实之量，分母是
，无论t
是实数或虚数，其平方都是实数。所以a 总不为虚数。但如设t
是一定轨道的周期时间，是一个实数，此一 S是天体在轨道上运
行的距离。则出现了这种情况，即各点之天体速度并不和其轨迹运行之距离相关，而只是关系于动点对场心的距离，(Kepler效应
或称Kepler第二定律) 。
Kepler's 2nd Law: The line between a planet and the Sun sweeps out equal areas in equal times.
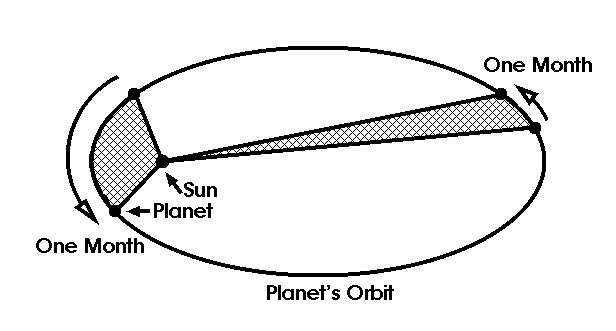
This law is a bit strange as stated, however, its meaning should become clear soon. In a weird way, it qualitatively describes the speed of a planet at different parts of its orbit.
椭圆轨道上各点的速度不相同，要按周期还原，不与 S之值相关的，于是 V非定值，V具有虚量。由于轨道运行方向之 a是虚量/实量=虚量。是 t为实即有 S为虚。于是构成轨道线加速度的时间与空间之间，有互为虚的关系，还是一个复变函数结构。
牛顿认为加速度是绝对值，他是对惯性系统之场源说的。即落体加速度和距场源之平方成反比，是一个实在一定之值。但天体轨道运行方向上之家速度不能是绝对值，它要受影响于对场心的距离和角度二者，还要受影响于各个非惯性系统。其值不可一定。即是一个虚量。故加速度有为实与为虚两种。
就普遍的天体运动而言，都不是直线的落体。它有对场心的距离和有运动方向的角度两个变化元，因而具有不定之值。其时间与空间的结构就必然是复变函数之结构。力是加速度所发生。而力只有万有引力具守常性，其它之力都不可说守常。故力的时空结构也是复变函数性质的。
(3) 作用：
f :
力
作用的物理量，表示一事件起的物理作用。
此式取 m为常量而只考虑其 V及 S。
作用是两个矢量
及
的积。凡两个矢量的积有标量矢量二种，计算作正圆运动之天体的作用，其动径为
r，转动线速度为? 
，取此之周期的时间 T为计算作用经过之时间，此运行一周之作用标量为?
，此量对外不存在，没产生何种实作用，是一个虚量。即此之时间虽为实，而其进行的距离?
只具虚数的性质，此之时间与空间相对为互虚。
另求其矢量积，作用
?? , 此之 S即 r是常实量。此之作用矢量实际存在，是垂直于?
及?? 
二矢量所构成之平面的。然而，因这个分母
T不论其经历多久，对作用并无所增减，T成了一个虚量，此之时空相对依然有互为虚的性质。
所以，物理作用的时空结构也是复变函数性质的。
(4) 天体运动诸元之关系
A）行星的动量动能关系
给行星 m以新的动量 mv’,
此行星原具动量
，设
? 及 
?
不同矢向，行星于是得有动量 
,而行星原有动能是 
，现之动能是
，
行星新的动量 
此式显示出天体动能动量的增量都要随夹角 
关系而变化，而动能属标量，非矢量，即
之空间对 
之空间，由能量关系来看，含有虚量。也即是两者的时间虽都为实，但空间有互为虚的关系，因而其时空结构是具有复变函数关系的。
由于 
K 为常数
这当其a为正值时，T是实时，但a若为负值，T就得为虚数。而a是正值是由场心出发来计算其动点距离之两的，这个周期T便和长半径之长度有关，同为实量。a之负值是从动点测其与场心距离之所得，是地球测它与太阳的距离并其周期之关系，此是从地球测天体之视动所得，于是不仅有太阳之关系，而全天之恒星都有比太阳差 1/365.24之日周期和年周期关系，这周期T所以就化为非实之数，如此之时空关系就成互虚的性质。
于是就得出一种普遍关系：在对一个场源上，a 和 T可以同是实数，在对广 泛无限多的天体上， a和 T即属互虚的。在非两体而是三体以上之天体的距离和周期之关系上都是带有复变函数的关系。
(5) 振动
振动的基本式? 
A：最大振幅 ω
：角速度这之间 t 可以有无限多个值对应于一个 X值，可以写为：
t：周期 k：一切整数
这可化成 
即空间距离 X所对应的正是带上虚系数的时间 t .
综合考察以上五项，是具有普遍性的时空组合。它们的时空结构无不存在复变函数之性质。而目前科学界对待它们，却极少知道用本文所指出的关系去认识，去了解其由此发生的诸多困惑与疑难。
三. 空间对空间的结构有虚与实的关系 ---(全文见 CosmicStructure1B)---
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑