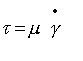 <11>
<11> 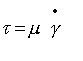 <11>
<11>
其中
t为应力,m为常数,g为应变,上面的点表示度时间求导数,对时间求导以后就成了应变率。在这个假设中,缺乏我们所需要的应力和应变本身的非线性关系,显然这是牛顿流体假设所限定的.近年来非牛顿流体得到了长足的发展,使得我们可以考虑,如何利用考虑非牛顿流体的办法来放宽这个限定.我们可以选用一种简单的非牛顿流体应力应变关系,并采用波尔兹曼叠加原理来构造应力和应变的关系,波尔兹曼叠加原理用于应力松弛表达可简单表述如下:1)应变是全部应力历史的函数,2)各个应变对应力的贡献是独立的,总应力是各个应变贡献的线性加和.若应变史是随时间连续变化的,则
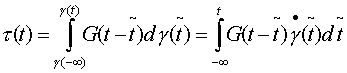
上式中G(t-t~)为松弛模量,对上式分部积分得
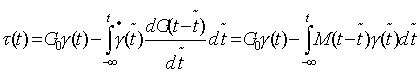
上式中M(t-t~)为记忆函数,它表示了一切线性粘弹性流体的力学性质.如果考虑的是麦克斯韦尔流体这样的非牛顿流体,在简单剪切流中,其微分型本构方程为:
![]() <12>
<12>
其中
t为应变张量元素,l是粘性系数和弹性模量的比.它代表流体内部应变的积累效应.所谓积累效应是指,在流动的每一个微应变距离上产生的微应力贡献都是要经过衰减的,然后叠加上新产生的应力.最后总的效应应当是这些不同位置上产生的应力又经过松驰衰减后的总和.对于稳定流动,从长时间平均的角度上来看,它会又回到牛顿流体的同构关系。解如上的微分方程,引入初始条件 t=-¥ ,
t=0 则可得:
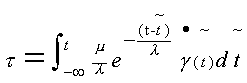 <13>
<13>
引入非牛顿流体应力关系式<13>以后,方程<9>就可以写成如下形式:
¶
V/¶ t+▽(V·V/2)+ W╳V = F-1/ρ▽P+ 1/ρ▽{t} <14>其中
t是个应力张量,上式也可以写成F+ F3 = -1/ρ▽{
t} <15>其中: F3 = -(¶ V/¶ t +1/ρ▽P +▽(V·V/2)+ W╳V)
= -(¶ V/¶ t +1/ρ▽P + V·▽V) <16>
F3表示出了流体中除了引力以外的其他的力:惯性力,压力,迁移加速度引起的惯性力,以及部分粘性力.
在上面的<15>式等号两边同时取对时间的偏微分得:
¶ F/¶ t+ ¶ F3/¶ t =- ¶ {1/ρ▽{
t}}/ ¶ t =- {1/ρ▽{¶ t/ ¶ t}} <17>利用式<19>得
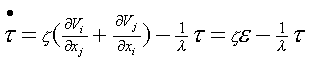
其中
x=m/l 把方程<17>中的¶ t/ ¶ t用上式代换,可得¶ F/¶ t+ ¶ F3/¶ t =- ¶ {1/ρ▽{
t}}/ ¶ t =- x▽{t}+1/r▽{t}于是有
¶ F/¶ t+ ¶ F3/¶ t=- x▽{e}-¶ F4/¶ t其中
F4=-▽{t}/l是由纯粘性张力贡献的那一部分力的变化?实际的微分结果说明,这一部分量值是很小的,第一部分是弹性的贡献,。注意到上式右段第一项为-
x▽{e}=- x▽{(¶ Vi/¶ xj+¶ Vj/¶ xi)eiej}=- x▽2{Vj eI}=- x [▽(▽· V)-▽´ ▽´ V]=x▽´ W
所以对不可压流就可以得到类似于电动力学方程3的表达形式如下:
¶ F/¶ t + ¶ F3/¶ t + ¶ F4/¶ t = ζ▽´ W <18>
这个公式的物理意义是引力和流体内各种内力的时间变化率和涡强度的旋度成正比.