物理科学探疑--网友天空--系统观点--王建华--第三章、对迈克尔逊--莫雷实验结果的新思考
![]()
第三章、对迈克尔逊——莫雷实验结果的新思考
王建华
第一节、S静止系与R运动系之间的运动时间变换系数βRT 。
在迈克尔逊—莫雷实验中,与坐标变换式相关的要素如下:
(1)、S静止系为宇宙真空坐标系。
(2)、R运动系为地球坐标系。
(3)、被观测事件为光子的运动。
(4)、光子上下的运动属于S静止系中的运动。而光子水平往返的运动则属于R运动系中的运动。
1、自R系观测,光子在R系中往返所需要的时间ΔTR 。
假设迈克尔逊—莫雷实验中,光子上、下、往、返的运动距离都等于d 。根据干涉仪实验的光路示意图,自R系(地球系)中观测,光子在R系中沿着XR轴往前运动距离XR=d,所需时间TR=d∕(Cs―U)。而光子沿着XR轴返回运动距离XR′=―d,所需时间TR′=―d∕[―(Cs+ U)]。
于是自R系观测,光子在R系中往返所需要的时间ΔTR为:
![]() (3―1)
(3―1)
2、自R系观测,光子在S系中往返所需要的时间ΔTRs
自R系观测,光子在S系中往前运动的距离XRs为:
![]()
由于自R系观测,光子在S系中往前运动的速率CRs=VR + U=Cs ,因此自R系观测,光子在S系中沿着 轴往前运动所需时间TRs为:
![]()
同理,自R系观测,光子在S系中返回运动的距离XRs′为:
![]()
由于自R系观测,光子在S系中返回速率CRs′=―(VR′+
U)=―Cs,因此自R系观测,光子在S系中沿着XR轴返回运动所需时间TRs′为:
![]()
于是自R系观测,光子在S系中往返所需要的时间ΔTRs为:
![]()
应该指出的是:在迈克尔逊—莫雷实验中,自R系观测,光子在S系中往返所需要的时间ΔTRs,与光子在R系中往返所需要的时间ΔTR相等即ΔTR=ΔTRs 。
物理学家们对迈克尔逊—莫雷实验结果的误解,就是由于把时间ΔTR误认为是时间ΔTRs了。时间ΔTRs与ΔTR虽然数值相等,但是两者的内涵是不同的。
3、自S系观测,光子在S系中上、下运动的时间ΔTs
自S系(宇宙真空系)观测,光子在S系中沿着Y轴上、下运动的距离都等于d 。于是光子在S系中上、下运动所需要的时间ΔTs为:
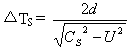 (3―2)
(3―2)
应该指出的是:光子在R系中往、返运动的距离d ,与光子在S系中上、下运动的距离d ,所使用的单位长度计量标准是完全相同的。又由于运动时间ΔTRs 、ΔTR和ΔTs三者中所使用的速率Cs和U完全相同,因此运动时间ΔTRs 、ΔTR和ΔTs三者所使用的单位时间计量标准是完全相同的。
根据经典物理学,自R系观测,光子在S系中往返运动的时间ΔTRs ,与光子在S系中上、下运动的时间ΔTs两者之差ΔT为:
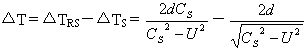 (3―3)
(3―3)
经典物理学认为:运动时间之差ΔT≠0。但迈克尔逊—莫雷实验结果证明:运动时间之差ΔT=0。这一事实表明:R系与S系两者运动时间之间,即时间ΔTRs与ΔTs之间,存在着一个使ΔT=0的变换系数。经典物理学的错误就是没有意识到ΔTRs与ΔTs之间存在着变换关系。
此外,时间之差ΔT=0这一事实还表明:ΔTRs与ΔTs两者单位时间的计量标准虽然是相同的,但ΔTRs、或ΔTs不经过变换系数改正时,两者在数值上是不能直接比较大小的。
4、光子在S系和R系两者中运动时间的变换系数。
假设光子在R系运动时间ΔTRs的改正系数为βRT ,在S系运动时间ΔTs的改正系数为βsT 。根据迈克尔逊—莫雷实验结果,可以得到下面两式。
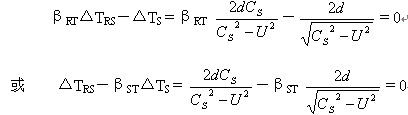
由上式可得到下面两式。
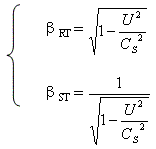 (3―4)
(3―4)
由上式可知,改正系数βRT与βsT互为倒数关系,即βRTβsT=1。而不是相等关系即βRT ≠βsT 。
5、把R系观测值ΔTRs变换成S系观测值ΔTS时,会出现“时慢效应”。
根据(3―4)式可以得到下面重要的结论:
自R系观测,由于光子在S系运动时间ΔTRs的改正系数βRT <1,因此光子运动时间ΔTRs,大于自S系观测得到的光子运动时间ΔTRs,即ΔTRs>ΔTs。
对于ΔTRs>ΔTs关系式来讲,如果把运动时间ΔTRs,改正变换为运动时间ΔTs,那么由于把ΔTRs变换成ΔTs时,会出现收缩现象(即βRTΔTRs=ΔTs),因此这一现象自S系角度来看(即观测者在S系中看),可以称为:R系运动时间的“时慢效应”。
(此“时慢效应”在迈克尔逊—莫雷实验中得到了验证。)
反之,如果把运动时间ΔTs,改正变换为运动时间ΔTRs,那么由于ΔTs变换成ΔTRs时,会出现膨胀现象(即ΔTs∕βRT=ΔTRs),因此这一现象自R系中看,可以称为:S系运动时间的“时快效应”。
应该指出的是,(3―4)式中的速率U是R系在S系中的速率,不是被观测事件的速率Vs 。然而在相对论变换式中,(3―4)式中的速率U却是被观测事件在S系中的速率。这显然是错误的。
正是由于相对论在理论上,把R系在S系中的速率U,错误的看成了是质点P在S静止系中的速率Vs
。才使得相对论在理论上出现了“双生子悖论”。
第二节、S静止系与R运动系之间的运动距离变换系数βRL 。
1、光子在S系和R系中运动距离。
根据干涉仪实验的光路示意图。自S系观测,光子上、下运动所需要的时间之和为ΔTs,而光子在S系中上、下运动的距离之和ΔXs为:
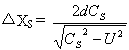
光子在R系中往前运动的距离XR=d 。然而,自R系观测,光子在S系中往前运动的距离XRs为:
![]()
光子在R系中返回运动的距离XR′=―d 。然而,自R系观测,光子在S系中返回运动的距离XRs′为:
![]()
光子在R系中往、返运动的距离之和ΔXR=2d。然而,自R系观测,光子在S系中往、返运动的距离之和ΔX Rs为:
![]()
根据经典物理学,光子在S系中运动的距离之和ΔXRs(自R系观测到的),与光子在S系中运动的距离之和ΔX s(自S系观测到的)之差ΔX 为:
 (3―5)
(3―5)
经典物理学认为:运动距离ΔXRs与ΔXs之差ΔX ≠0。但迈克尔逊—莫雷实验结果证明:运动距离之差ΔX =0。这一事实表明:运动距离ΔXRs与ΔX s之间存在着一个使ΔX =0的变换系数。
经典物理学的错误就是没有意识到,ΔX Rs与ΔXs之间存在着变换关系。此外也没有意识到,ΔX Rs是自R系观测到的,光子在S系中运动的距离之和。
距离之差ΔX =0的实验结果表明:虽然运动距离ΔX Rs与ΔX s,两者单位长度的计量标准是相同的,但由于前者是自R系观测到的,而后者是自S系观测到的,因此两者不经过坐标式变换时,在数值上是不能直接比较大小的。
2、S系与R系两者运动距离的变换系数。
假设运动距离ΔX Rs的变换系数为βRL ,而运动距离ΔXs的变换系数为βSL
,那么根据迈克尔逊—莫雷实验结果,可以得到两个使ΔX =0的关系式。
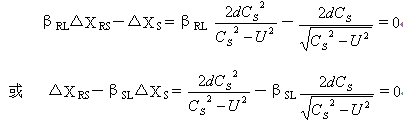
由上式可以得到下面两式。
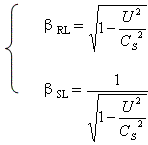 (3―6)
(3―6)
应该指出的是:(3―6)式与(3―4)式实质上是同一个关系式即
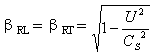
或者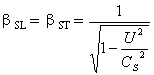
由于系数βRL是运动距离的变换系数,而βRT是运动时间的变换系数,因此距离变换系数与时间变换系数是同一个变换系数。这一分析推证结果与前面第二章中利用解线性方程方法,推证出的结果是一致的。
3、把R系观测值 ( X R+ U TR )变换成S系观测值XS时,会出现“尺缩效应”。
自R系观测,光子在S系中的运动距离X RS=X R+ U TR。根据(3―6)式可以确定:由于变换系数βRL<1,因此运动距离X RS大于运动距离X S,即X RS>X S 。
对于X RS>X S关系式来讲,如果把运动距离X RS,变换为运动距离X S,那么由于X RS变换成X S时,会出现收缩现象(即βRLX RS=X S),因此这一现象从S系角度看,可以称为:R系运动距离的“尺缩效应”。(尺缩效应在迈克尔逊—莫雷实验中得到了验证。)
反之,如果把运动距离X S,变换为运动距离X RS,那么由于X S变换成X RS时,会出现膨胀现象(即X S∕βRL=X RS),因此这一现象自R系中看,可以称为:S系运动距离的“尺胀效应”。
4、物理学家对“尺缩时慢”效应的解释是错误的。
为了解释麦克尔逊-莫雷实验结果,斐兹杰诺和洛仑兹先后提出过
“尺缩时慢”的假说。他们认为:一切物体都要在它的运动方向上收缩,即相对于以太运动的钟走慢了、尺长缩短了。
在麦克尔逊-莫雷实验中,地球是运动的,而以太(宇宙真空系)是静止的,由此洛仑兹-斐兹杰诺才提出了“尺缩时慢”这一假说。该假说显然是站在宇宙真空系的角度,来解释麦克尔逊-莫雷实验结果的。
按照斐兹杰诺给出的“尺缩时慢”定量关系,当火箭速率达到光速的一半时,火箭长度在运动方向收缩百分之十五。当火箭速率达到每秒26万公里时,收缩百分之五十,也就是说原来1米长的尺,现在只有五十厘米了。
然而,我们在第二章中曾经分析证明过,物体在惯性系中运动时,它自身的长度不会发生任何的变化。由于洛仑兹-斐兹杰诺不知道麦克尔逊-莫雷实验中 “尺缩时慢”的效应,在本质上是所观测到的物体运动距离和运动时间的收缩,不是物体自身长度的收缩,因此他们的“尺缩时慢”假说应修改为:当R系运动距离变换成S系运动距离时,那么R系运动距离和运动时间就会在运动方向上出现收缩。
5、“尺缩时慢”效应不具有相对性。
由于两个物体之间的运动是相对运动,即自R系观测,S系在R系中的速率为-U,因此物理学家们相当然地认为:“尺缩时慢”效应具有相对性,即自S系看,R系的时空坐标“尺缩时慢了”。反之,自R系看,S系的时空坐标也同样地“尺缩时慢了”。
然而,在麦克尔逊-莫雷实验中,自R系(地面系)观测时,光子在S系(宇宙真空系)中的运动距离ΔX RS(或者运动时间ΔT RS),比自S系观测时,光子在S系中的运动距离ΔX S(或者运动时间ΔTS)大,即:ΔX RS>ΔX S,ΔT RS>ΔTS 。
或者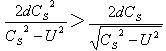
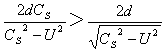
上式关系式显示,自R系看,S系的时空坐标是“尺胀时快了”。而不是“尺缩时慢了”。由此可以确定:“尺缩时慢”效应不具有相对性。物理学家们关于“尺缩时慢”效应具有相对性的看法是错误的。
第三节、高速粒子简单近似的坐标变换式。
把(3―6)式代入(2―12)式,可得到S系运动距离XS,与R系运动距离(
XR+ UTR )的近似变换式。
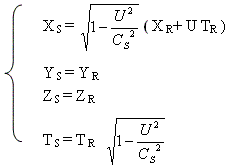 (3―7)
(3―7)
或
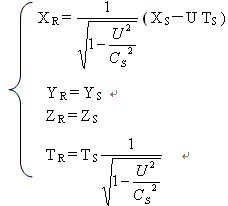 (3―8)
(3―8)
应该指出的是:上面两式中的变换系数,是在观测事件为光子这一条件下推证出来的。从这一点讲,上面两式仅仅适用于高速运动物体的坐标变换,不适用于低速运动物体的坐标变换。
当质点P是低速运动的物体时, R系与S系两者坐标变换所使用的变换式是另外的新变换式。而上面的(3―7)式和(3―8)变换式,是新变换式在一定条件下的简化式。(有关新变换式的详尽推证请看第六章)。
利用(3―7)式可以把光子R系的时空坐标(X R、0、0、TR),变换成S系的时空坐标(X
S、0、0、T S)。
同理,利用(3―8)式可以把光子S系的时空坐标(X S、0、0、T
S),变换成R系的时空坐标(X R、0、0、TR)。
(3―7)式和(3―8)式在数学转换关系上,是完全符合数学运算法则要求的。由于相对论变换系数中没有包括,R系在S系中的速率U,因此相对论变换式实质上是一个错误的变换式。
第四节、迈克尔逊—莫雷实验证明了宇宙真空系就是绝对静止系。
1、相对论否定绝对静止系存在的理由。
为了验证“以太粒子” 假说是否正确。1881年麦克尔逊专门进行了著名的麦克尔逊—莫雷实验。根据计算出的光子水平往返运动时间与上下运动时间之差ΔT(ΔT≠0)。麦克尔逊认为通过干涉实验可以很容易地看到,两束相干光的干涉条纹移动。但迈克尔逊—莫雷实验的结果是,看不到有明显的干涉条纹移动。即运动时间之差ΔT=0。
于是“以太”假说遭到了实验结果的否定。由此人们确定:在宇宙空间不存在绝对静止的,并且与物质粒子没有任何相互作用的“以太”粒子。
为了解释麦克尔逊-莫雷实验结果,爱因斯坦提出了“光速不变原理”假说。根据光速不变原理,自地面参照系中观测,光子在地面参照系中的速率都等于宇宙真空中的光速C
。光子沿着地球运动方向往返运动的时间与光子上下运动的时间之差就等于0。无论将麦克尔逊干涉仪转动多少度,干涉条纹都不应该发生移动。
光速不变原理包括两项原则,即光速在惯性系内是常量和光速与源速无关。这两条原则如果同时成立,则必然导致牛顿绝对时空观的崩溃。由于麦克尔逊-莫雷实验是在地面上进行的,而实验结果始终接近于零,因此人们根据实验结果很容易地误认为:光速在惯性系内是一个常量。又根据电磁理论“光速与光源的运动无关”,因此物理学家们认为,牛顿力学中的绝对静止系是不存在的。
然而麦克尔逊-莫雷实验结果事实上,是否定“光速在惯性系内是常量”这一假说的。人们之所以认为:麦克尔逊-莫雷实验结果证明了“光速在惯性系内是常量”这一假说,是因为人们对实验结果本质不了解,是人们对事物运动规律的一种误解。这就如同历史上人们曾经误认为,地球是宇宙的中心一样。本文下面分析讨论一下这个问题。
2、地面上的光速CR不等于宇宙真空中光速C的理论证明。
自S系观测,光子在S系中的运动距离为X S,运动时间为TS。于是自S系中观测,光子在S系中的速率CS为:
CS=d X S∕d TS=X S∕T S
同理,自R系观测,光子在R系中的运动距离为X R ,运动时间为TR。于是自R系中观测,光子在R系中的速率CR为:
C R=d X R∕d T R=X R∕T R
根据(3―7)变换式可知,自R系观测,光子运动距离的变换式为:
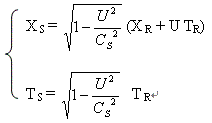
把上面两式对时间TS 微分后得关系式
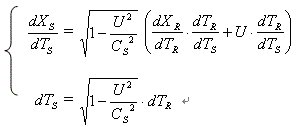
由上式得下面的关系式:
![]()
上式表明:光子在S系中的速率CS等于光子在R系中的速率CR,与R系在S系中的速率U之和。由上式得光子在R系中的速率CR即:
CR=CS―U
上式表明:当R系(地球系)在S系(宇宙真空系)中的速率U≠0时,那么光子在R系中的速率CR就不等于光子在S系中的速率CS(宇宙真空中的光速C),即CR≠C
S 。并且光子在R系各方向上的速率是不相等的。
由于地球在宇宙中的速率U≠0,因此光子在地球上的速率CR≠光速C。并且根据CR=C―U关系式,光子在地面上各方向上的速率是不相等的。由此可以确定:地球系不是绝对静止系。
3、宇宙真空系就是绝对静止系的理论证明。
我们在匀速运动的火车上用相等的力,向各方向上投掷同一个物体时,物体被投掷出的距离是相等的。由此可以确定:匀速运动的火车系就是惯性系。然而,如果我们自地面上观测物体被投掷出的距离时,那么可以确定:物体被投掷出的距离是不相等的。从这一点讲,火车系就不是绝对静止系。
由于光子运动的速率与发光源的运动状态无关,因此从理论上讲,当光子在某一个惯性系各方向上的速率都等于光速C时,那么这个惯性系即为绝对静止系。
自S系(宇宙真空系)中观测,光子在S系中沿着Y轴上或下的运动距离都是d 。于是自S系观测,光子在S系上、下运动所需要的时间TS为:
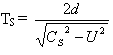
光子在R(地球系)系中往前运动的距离XR=d 。而自R系观测,而光子在S系中往前运动的距离XRS为:
![]()
光子在R系中返回运动的距离XR′=―d 。而自R系观测,光子在S系中返回运动的距离XRS′为:
![]()
光子在R系中往、返运动的距离之和ΔXR=2d 。而自R系观测,光子在S系中往、返运动的距离之和ΔXRS为:
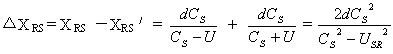
根据(3―7)变换式得关系式
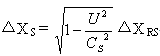
光子在S系(宇宙真空系)中运动的速率XS/ T S为:
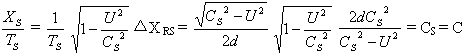
历史上许多人在不同季节、不同时刻、不同方向上反复地做过麦克尔逊-莫雷实验。特别是近些年来,利用激光使这个实验的精度大为提高,但是所得到结论却没有任何变化。这一事实表明:光子在宇宙真空中的每一方向上的速率都等于光速C。由此可以确定:宇宙真空系就是绝对静止系。
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑