弦状理论Strings theory

物理科学探疑-网友天空-原子原子核-弦状理论
wytk-11.gif (489 字节)

弦状理论
Strings theory

熊玉科
山东省菏泽学院 274000

关键词：自旋康普顿波纵场横场
key words：spin Compton wave longitudinal field crosswise field

摘要：粒子周围的场随粒子一同转动，由狭义相论可以论证：
i）场的纵向分量的作用范围可达无穷远称为纵场；场的横向分量变弯且会限制在半径r_max= c/ω 的圆柱形范围内，称为横场；这就解释了为什么会有长程力和短程力。
ii)康普顿波的本质就是粒子的横向力程，某个只有一个ω的基本粒子，按照狭义相对论和量子力学对能量的表述有：E=mc²= hω变形后得 /mc=c/ω所以核力力程 r= h/mc=c/ω。

Abstract：the field of particle turns round with it’s spin together through the special theory of Relativity can prove：

1）The longitudinal field of force can extend to infinite distance,We name it as longitudinal field,Transeral field of force Can bend and be confined in the Column which radius is r_max= c/ω, We name it as crosswise field，So we can explain the long and short distance force
2)Nature of Compton Wave is the lougest distance of transversal field as mc²= hω Seek to prove h/mc=c/ω distance of nucleic is r= h/mc=c/ω

弦状理论的求证

对于只有一个自旋量的粒子,相对某参照系静止，此时粒子没有热运动，在这种情况下，我们认为狭义相对论和量子力学仍然成立。

根据狭义相对论和量子力学对能量的描述有：

xzhll002.gif (5357 字节)

众所周知 λ= /mc的意义是粒子的康普顿波长的表达式，而右边又怎么理解呢？

不防作以下推断：粒子的自旋就是粒子绕中心轴作经典的转动，同时粒子周围的的场也一同转动。
考察粒子“赤道”截面上某一点，其半径为r，该点场的线速度为rω；依据光速极限原理可知rω≤c，其极值r_max= c/ω

而粒子“两极”的场可以延伸到无穷远，总结如下：对于只有一个自旋量的粒子且相对于某参照系静止，粒子的场分布在一个半径为c/ω(或 h/mc)无限长的圆柱内。

远观粒子场就像一条“琴弦”。这就能够解释为什么会有长程力和短程力，从而证明了弦状理论。

弦的长度和速度及热转动的关系

仍然选择只有一个自旋量的粒子为例，由于粒子之间无规则碰撞，弦开始热转动，速度越大的粒子从统计的角度讲转动也快，静止时粒子无限长，由光速极限原理可知：

rω≤c ∴r≤c/ω，这里的ω为热自旋量，不同于内禀自旋，显然温度超低，ω越小，粒子越长，ω接近于零其长度趋向无限长，粒子能量越大时，ω也变大，粒子变短，粒子性就很明显。

应用例一：

定性解释电子单缝实验中的明暗条纹成因

由于电子场是一个细长圆柱体或说是一条弦，当它垂直入射光屏时，作用面积最小电子轻易地进入荧光屏内部而不发光或很弱，当电子平等碰撞荧光屏时，作用面积最大，作用力最大，负加速度最大，由电动力学知，电子辐射强度与加速度的平方成正比，因此形成亮点。

这可以跟一个宏观实验相类比，一个木棒从高空落下，垂直进入水时阻力最小，平行入射时作用力最大，跳水运动员从高空下落总是手和头向下，身子与水面垂直下落，若平行下落，身子会受到较大冲击，隧道效应，势垒贯穿也是这个道理。

应用例二：

单粒子的运动方程

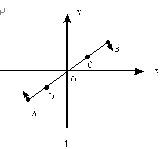
用AB表示某低速自由(势能为零)粒子从左向右运动，速度为V同时做旋转运动，角速率为ω。

AB长度可以由光速极限原理求得AB≤2 c/ω，OB=OA= r

特别强调这里的ω是热转动而不是内禀自旋

因此有：中心0点：x=vt

A点：rA=r(cosωt+sinωt)，

B点：rB=r［cos(ωt+π)+sin(ωt+π)］，

ω过大时粒子变弯呈“S”形

参考文献1［美］E、H威切曼著，1971《量子力学》科学技术出版社P₂₄₇
参考文献2 褚圣麟，1983《原子物理》高等教育出版社P₃₂₅

返回首页