物理科学探疑-网友天空-分子原子原子核-气体分子运动论新观念
![]()
气体分子运动论新观念
芦光耀
摘要:本文的主要目的是要证明一条新的气体定律,即,在平衡态下,气体分子沿某一方向运动的平均速率等于声速。本文从分子运动的角度阐明声波在气体中的传播原理,依据该原理导出的气体声速计算式与热力学教材中所导出的气体声速计算公式完全一致。本文标题中的新观念,是指从粒子运动的角度来认识波的传播。
关键词:能量等效,位移等效,分子的振动接力,纯理想气体。
在平衡态下,人们通常认为气体分子在作无规则运动,但平均地来说,可把气体分子的运动分解为振动加线性运动,线性运动指分子沿某一方向作直线或曲线运动。通常,分子线性运动的能量远小于其振动的能量。
一、声音在气体中的传播原理
为说明声波在介质中传播的概念,我们先来做一个实验。
现有5个振子,它们的质量、大小、振动频率都相同,设它们彼此反相振动,而且它们的振幅是刚好使它们相碰,也就是说,它们是相互碰撞的,如图1所示。
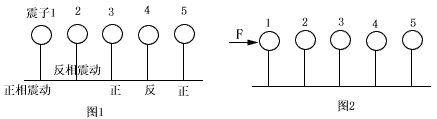
在该振动系统工作时,各振子只做振动而不传递任何信息。设该振动系统工作,现在,通过一外力F使振子1产生一附加位移△x,如图2所示。那么,在△t时间内,这一附加位移△x将通过其它振子的接力而传递到振子5。那么,在△t时间内,附加位移△x通过振子的振动接力,从振子1传递到振子5的过程就是波的传播过程。显然,如果把5个振子的振动频率同时加大,那么,附加位移△x的传播速度就会加快,也就是说,振子的振动频率越高,波的传播速度就越快。
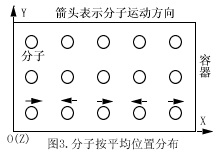
 声波在气体中就是依靠分子的振动接力而传播的。我们知道,气体分子运动的特点就是分子之间的相互碰撞,而一般来说,相互碰撞都含有粒子之间的反相运动成分,而且这种碰撞的效果使气体内的能量和粒子的位置趋于均匀分布,这都是粒子振动所具有的特性。平均地来说,把气体分子的运动分解为振动加线性运动是和实际气体分子运动的平均效果等效的。由于我们的目的是要求解气体分子运动的平均速度,因此可采用下述的物理模型进行计算。设一容器内的分子数为N,分子质量为m。首先,我们我们进行能量等效,即把容器内所有分子的总能量平均分配给每一个分子,因而每一个分子都具有相同的能量,这样做,总能量是等效的。其次,我们进行位移等效。在平衡态下,所有分子线性位移的矢量和必为零,因为如果这个矢量和不为零的话,将出现气体流动现象,这与平衡态的概念不符。由于在平衡态下,所有分子线性位移的矢量和为零,因此,容器内分子的运动可看成是在某一固定点附近作等幅反向振动,这样做,总位移是等效的。这样,平均地来说,我们可以把所有分子均匀地摆放在容器中,而这些分子都在它们的平衡位置附近作反向等速振动,如图3所示。图3是描写分子在X轴方向上的运动,沿X轴方向,这些分子彼此反向运动,且运动速度的大小都相同。这样,沿X方向,它们彼此相互碰撞,由于碰撞速度的大小都相同,因此,它们都在平衡位置附近作振动。由于气体的性质与方向无关,因此分子沿X、Y、Z方向的运动情况相同。
声波在气体中就是依靠分子的振动接力而传播的。我们知道,气体分子运动的特点就是分子之间的相互碰撞,而一般来说,相互碰撞都含有粒子之间的反相运动成分,而且这种碰撞的效果使气体内的能量和粒子的位置趋于均匀分布,这都是粒子振动所具有的特性。平均地来说,把气体分子的运动分解为振动加线性运动是和实际气体分子运动的平均效果等效的。由于我们的目的是要求解气体分子运动的平均速度,因此可采用下述的物理模型进行计算。设一容器内的分子数为N,分子质量为m。首先,我们我们进行能量等效,即把容器内所有分子的总能量平均分配给每一个分子,因而每一个分子都具有相同的能量,这样做,总能量是等效的。其次,我们进行位移等效。在平衡态下,所有分子线性位移的矢量和必为零,因为如果这个矢量和不为零的话,将出现气体流动现象,这与平衡态的概念不符。由于在平衡态下,所有分子线性位移的矢量和为零,因此,容器内分子的运动可看成是在某一固定点附近作等幅反向振动,这样做,总位移是等效的。这样,平均地来说,我们可以把所有分子均匀地摆放在容器中,而这些分子都在它们的平衡位置附近作反向等速振动,如图3所示。图3是描写分子在X轴方向上的运动,沿X轴方向,这些分子彼此反向运动,且运动速度的大小都相同。这样,沿X方向,它们彼此相互碰撞,由于碰撞速度的大小都相同,因此,它们都在平衡位置附近作振动。由于气体的性质与方向无关,因此分子沿X、Y、Z方向的运动情况相同。
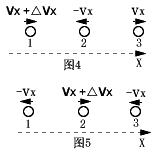
声波在气体中的传播,可用分子对速度增量的传播来描述。设分子沿X方向的平均振动速度为Vx,由于某种原因使分子1在某一时刻的速度增加了△Vx,如图4所示。由于分子1和分子2的质量相同,由碰撞理论可知,分子1和分子2发生弹性碰撞后,两者将彼此交换速度,也就是说,碰撞后,分子1将以-Vx运动,而分子2将以Vx+△Vx运动,如图5所示。同样,分子2和分子3碰撞后,彼此交换速度,分子2将以-Vx运动,分子3将以Vx+△Vx运动,这样,速度增量△Vx将通过分子的振动接力而传播出去,而分子沿X方向的平均振动速度Vx就是声波沿X方向的传播速度。
实际中,虽然分子存在着线性位移,但不管分子线性位移到了那一点,该分子和其周围分子仍然存在着振动接力的关系。从能量的角度来看,由于在平衡态下,通常,分子线性运动的能量远远小于其振动的能量,因而也可忽略分子的线性运动。
我已初步证明,电场、磁场、重力场是由同一种物质作不同类型的运动而形成的;换句话说,它们是同一种物质的三种形态。我命名这种物质为“R物质”。如果不考虑气体分子之间的相互作用,那么“R物质”微粒的运动状态和气体分子很类似。光波也是依靠“R物质”微粒的振动接力而传播的,由图1的实验可知,“R物质”微粒的振动频率极高,因而光波的传播极快。如果“R物质”微粒的平均振动频率不变,则光速就为常数。这一点就解释了为什么光在“真空”中的速度为常数。注意,这里所说的“真空”是教科书的说法,人们通常认为的“真空”是存在“R物质”的。我之所以说初步证明了“R物质”的存在,是因为我对此只作了定性的证明,还没做到定量的描述,而这又涉及到对大量粒子运动规律的定量描述。我本想用现有的教科书中的分子运动论来描述“R物质”运动,但发现现有理论并没有从分子运动的角度对声波的传播和传播速度作出解释。这说明目前的分子运动论还不完善。我写这篇文章的目的就是为了补充和完善分子运动论,同时,这也是我对“R物质”存在作定量证明所走出的一步。另外,人们对光具有波粒二象性觉得难于理解,其实,人们在现实中能够感受到的波都是波粒二象性的,比如水波,传播介质是水,而水是由水分子所组成的,因而水波是波粒二象性的,同样,声波也是波粒二象性的。波粒二象性中的粒子性就是指的传播介质,没有传播介质,波是不可能发生的。比如水波,如果没有传播介质水,则水波就不可能发生。因此,波的准确定义应当是,振动在介质中的传播叫做波。
二、压强公式推导
我们知道,压强是大量气体分子对器壁的碰撞而产生的。假设有一长方形容器,长、宽、高分别为l1、l2、l3,容器内所贮气体的总分子数为N,每个分子的质量为m,取直角坐标系OXYZ,如图6所示。
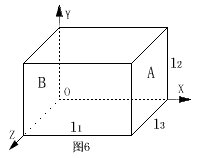
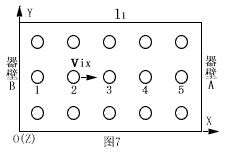
按照前面所述,我们把容器内的所有分子均匀地摆放在容器中,如图7所示。下面定量推导垂直于X轴的器壁A所受到的压强。
先来考虑一个分子对器壁A的冲量。设容器内的所有分子都在它们振动时的平衡位置静止不动。现在让容器内的某一分子以速度Vi运动,Vi的三个分量为Vix、Viy、Viz,由于三个分量中只有Vix对分子与器壁A的碰撞有贡献,因此,就对器壁A的碰撞来说,可只考虑分子沿X方向的运动,也就是说,可以设Viy、Viz为零。设分子2以Vix向器壁A运动。分子2将首先与静止的分子3相碰,由于分子的质量都相同,由碰撞理论可知,碰撞后,分子2将停留在分子3的位置,而分子3将以速度Vix撞向分子4,这样,就形成了分子的接力运动,接力运动到分子5时,分子5以速度Vix与器壁A相碰,这种接力运动就相当于容器内分子2单独存在时(即:容器中只有一个分子存在的情况),该分子以速度Vix与器壁A相碰。这样,分子2从2位置出发到与器壁A相碰,然后返回到位置2,再从位置2运动到器壁B,再返回到位置2,此时,分子2就完成了与器壁A的一次碰撞循环。分子2的一次碰撞循环所经过的路程应为2l1,请注意,这是在没考虑分子体积时所得出的结论。在考虑分子体积时,上述结论是否精确呢?下面就来分析一下这个问题。由于在平衡态下,各分子都在其固定的平衡位置附近作振动,因此,当分子2以速度Vix与静止的分子3相碰后,一定是发生了位置替换。也就是说,碰撞后,分子2的质心停留在了碰撞前分子3的质心位置处,这就相当于质点碰撞的情况,因此在考虑分子体积时,上述结论仍然精确。以下的推导过程和物理教材(注1)基本一致,现简述如下。
分子2与器壁A碰撞一次施于器壁的冲量为2mVix,因此,在△t时间内,分子2施于器壁的冲量为:
![]()
这理要说明一点,如果在图7中将分子2的速度方向取反,也就是说,分子2以-Vix向器壁A运动,则在△t时间内,分子2施于器壁A的冲量仍为上面表达式。
对所有的N个分子求和,可计算出在△t时间 内N个分子施于器壁A的总冲量为:
![]()
大量分子对器壁A的碰撞使器壁A受到了一个持续恒定的力F,设F的持续作用时间为△t,则△I=F·△t,即F=△I/△t,将F除以器壁A的面积l2l3,可求得压强为:
![]()
将上式分子分母同乘以分子总数N,得:

请注意,![]() 就是声波在气体中沿X方向的传播速度。在等效物理模型中,容器内所有分子彼此反向振动,振动速度的大小都是
就是声波在气体中沿X方向的传播速度。在等效物理模型中,容器内所有分子彼此反向振动,振动速度的大小都是![]() 。
。
需要说明的是,虽然(8)式与物理教材中压强表达式相同,但这里的![]() 与教材中所说的
与教材中所说的![]() 有所不同,这里的
有所不同,这里的![]() 表示容器内的每一个分子沿x方向的运动速率都为
表示容器内的每一个分子沿x方向的运动速率都为![]() ,因而
,因而![]() 是可以进行开方运算的。
是可以进行开方运算的。
在平衡态下,按教科书的推理,分子三个速度分量平方的平均值必然相等,即:
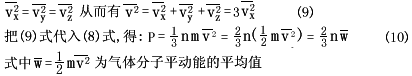
三、纯理想气体与实际气体的差别
为叙述方便,我们把上面(10)式所描述的气体叫做纯理想气体,从上面的推导过程可知,纯理想气体只涉及粒子的弹性碰撞,其压强为:
![]()
而物理教材中提到的公式P=nkT (11) (式中的k为玻耳兹曼常数,T为气体的热力学温度)
由于(11)式是由实验公式推导而来,因此它应属于实验公式,在一定范围内,基本反应真实气体的性质,因此,对于真实气体,我们就用(11)式来表达。
我们的目的是用纯理想气体来描述真实气体,那么,(10)式与(11)式是否等价呢?要搞清这个问题,首先应搞清纯理想气体和真实气体之间的差别。真实气体分子之间存在着相互作用,而纯理想气体分子之间是完全的弹性碰撞。真实气体可以从外界吸收热量,或向外界辐射热量,而纯理想气体不具有这种功能,也就是说,纯理想气体不涉及热量的吸收或辐射。由于热力学第一定律是对真实气体的描述,因此,纯理想气体肯定不符合热力学第一定律。显然,由于上述差别的存在,(10)式与(11)式是不等价的。那么,如何用纯理想气体来描述真实气体呢?我们采用添加系数的方法,即令:
![]()
也即:P=αP′ (12)
式中的P为真实气体的压强,P′为纯理想气体的压强,α就是添加的系数,假定在实验公式(11)式的适用范围内α为常数。下面就来求解α。
首先,把纯理想气体的压强公式(10)改写为下面形式,
![]()
式中的N为体积V内的分子总数。现对纯理想气体进行准静态压缩,然后根据热力学教材(注2)对压缩系数的定义解出压缩系数。对(13)式两边取微分,
![]()
经理得,纯理想气体的压缩系数为:
![]()
由于准静态压缩代表无限缓慢的理想压缩过程,以至在压缩过程的每一时刻,气体都处于平衡态,在该种情况下,由碰撞理论可知,气体分子对器壁的碰撞,在碰撞前后,分子在与器壁垂直方向速度的大小保持不变,因此(14)式中速率对压强的变化为零,于是(14)式可简化为:
![]()
也就是说,纯理想气体的压强只是体积的函数。由于纯理想气体不涉及热量的吸收或辐射,因此,纯理想气体在压缩时不向外界辐射热量,而真实气体在绝热压缩时也不向外界辐射热量,因此,这两个过程对外界的作用是等效的。在对外界等效的情况下,我们用纯理想气体来模拟真实气体,也就是,令,纯理想气体的压缩系数等于真实气体的绝热压缩系数,这样就可解出系数α,热力学教材提出的真实气体的绝热压缩系数为:
![]()
式中s表示绝热,γ为真实气体的定压摩尔热容量与其定容摩尔热容量之比。
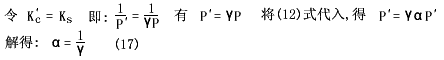
求解系数α还有第二种方法,现简述如下。我们还是采用纯理想气体的压缩来模拟真实气体的压缩。对真实气体的压缩有两种方法,一是等温压缩,二是绝热压缩。显然,要实现对真实气体的准确模拟,既要符合其等温压缩,又要符合其绝热压缩。由于纯理想气体的压缩和真实气体的绝热压缩都不向外界辐射热量,即,这两个过程对外界的作用等效,因此,我们令纯理想气体的压缩系数等于真实气体的绝热压缩系数,即:
![]()
然后,考虑符合真实气体等温压缩的要求。真实气体的等温压缩系数为:
![]()
(3b)式是对上面的(11)式进行微分运算而导出,这里就省去推导过了。把上面的(12)式代入(13)式得:
![]()
整理后得,真实气体的等温压缩系数应满足:
![]()
![]()
把(3c)式代入(3a)式也可解出系数α。
将(17)式代入(12)式,得真实气体的压强为:
![]()
从(11)式和(18)式中消去压强P可得分子平动能的平均值,即:
![]()
把(19)式代入(18)
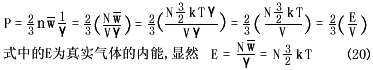
以上讨论的真实气体是指单原子气体。![]() -
-![]() /γ代表分子损耗,初步分析,该损耗应来自两方面,一是分子之间的相互作用而产生的损耗,二是分子辐射而产生的损耗。既然存在分子损耗,在平衡态下,必有来自外界的能量来补充这种损耗,也就是说,在平衡态下,平均地来讲,单位时间内,分子从外界吸收的能量等于其损耗的能量。
/γ代表分子损耗,初步分析,该损耗应来自两方面,一是分子之间的相互作用而产生的损耗,二是分子辐射而产生的损耗。既然存在分子损耗,在平衡态下,必有来自外界的能量来补充这种损耗,也就是说,在平衡态下,平均地来讲,单位时间内,分子从外界吸收的能量等于其损耗的能量。
(20)式表明,如果以kT的形式来表达气体内能的话,则γ不参与内能的计算。如果计算分子损耗的话,按能量以自由度均分的原则,气体分子每自由度的损耗应为:
![]()
四.声速公式推导
本文的目的就是要证明一条新的气体定律,即:在平衡态下,气体分子沿某一方向运动的平均速率等于声速。
现把气体压强的理论计算式(18)式和实验公式(11)式重写如下,
![]()
从上两式中消去压强P即可得出气体分子沿某一方向运动的平均速率,即声速为:
![]()
式中R:普适气体恒量。T:气体的热力学温度。μ:气体的摩尔质量。
γ:气体的定压摩尔热容量与其定容摩尔热容量之比。
式(22)式与热力学教材(注2)所导出的气体声速计算公式完全一致。
热力学教材还给出了下面气体声速计算公式,即:
![]()
式中w为声速,ρ为气体密度,ks为气体的绝热压缩系数。利用该公式,我们可以计算一下纯理想气体的声速。由上面的(13)式可知,纯理想气体的压强也可表达为:
![]()
由于纯理想气体在压缩时不向外界辐射热量,因此,由上面(15)式表达的纯理想气体的压缩系数也是其绝热压缩系数。把(15)式代入上面的(5a)式,再根据(5b)式得:
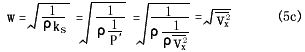
前面曾经说过,![]() 是可以进行开方运算的,因此,纯理想气体的声速应为:
是可以进行开方运算的,因此,纯理想气体的声速应为:
w = ![]() (5d)
(5d)
也就是说,对于纯理想气体来说,在平衡态下,气体分子沿某一方向运动的平均速率等于声速。这也与前面对纯理想气体的描述是一致的。
五.气体分子的平均振动频率和周期
气体分子沿X、Y、Z方向的平均距离是相等的,设分子沿X方向的平均距离为![]() ,按统计规律,分子沿X、Y、Z方向的碰撞频率也是相同的,设分子沿X方向的碰撞频率为
,按统计规律,分子沿X、Y、Z方向的碰撞频率也是相同的,设分子沿X方向的碰撞频率为![]() 。设有一速度增量信号△Vx沿X方向从1点经时间t传播到了5点,如图10所示。
。设有一速度增量信号△Vx沿X方向从1点经时间t传播到了5点,如图10所示。
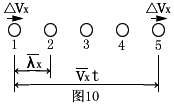
![]() ·t为t时间内△Vx所走过的路程,
·t为t时间内△Vx所走过的路程,![]() ·t为t时间内分子之间发生的碰撞次数。由于△Vx是依靠分子之间的接力运动而传播的,因此,t时间内的碰撞次数就是该时间内的接力次数,而接力次数就是
·t为t时间内分子之间发生的碰撞次数。由于△Vx是依靠分子之间的接力运动而传播的,因此,t时间内的碰撞次数就是该时间内的接力次数,而接力次数就是![]() 的数量,因此有:
的数量,因此有:
![]()
![]()
![]()
![]()
因此,平均碰撞频率![]() 与方向无关。同样,可证明分子的平均振动周期
与方向无关。同样,可证明分子的平均振动周期![]() 和平均振动频率
和平均振动频率![]() 也是与方向无关的。分子的平均振动周期为分子往返一次运动所需要的时间,由图10可知:
也是与方向无关的。分子的平均振动周期为分子往返一次运动所需要的时间,由图10可知:
![]()
分子的平均振动频率为分子在1秒钟内的平均振动次数,即:
![]()
![]()
即:分子的平均碰撞频率为平均振动频率的2倍。
![]()
![]()
这里所说的分子的平均碰撞频率是指在声波的传播过程中,分子在1秒钟内所发生的接力次数。
注1:物理教材为参考文献1。
注2:热力学教材为参考文献3。
作者:芦光耀
2009年1月7日
单位:待业
住址:北京市丰台区东高地三角地37栋丁门四楼111号
邮编:100076
电话(Tel):68751647
E-mail:hulahuaer@hotmail.com
参考文献
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑