物理科学探疑-网友天空-宇宙的观念-牛顿万有引力定律是错误的
牛顿万有引力定律是错误的
——我发现并创立了一种新的行星运动理论——
济南市花园路5号 王建华 著
论文目录及提要：
文章序言、（2～5页）
内容提要：首先在序言一中指出了哥白尼“日心说”运动模型存在着一个重大的理论缺陷。为了修正这一理论缺陷，本文在理论上提出了“太阳系质心说”（或“恒星系质心说”）运动模型。其次在序言二中指出了“新的行星运动理论”是建立在四个基石之上的。最后在序言三中指出了牛顿分析研究引力定律的起点，不属于对客观事实直接观测的结果，而是属于可能包含有人工误差的观察定律。而本文分析研究新引力定律的起点，则属于对客观事实直接的、正确的观测结果。
第一节、太阳和所有的行星都是绕太阳系质心运动的。（5～5页）
内容提要：本文把太阳系看成是一个质点系统。利用质点系统质心的定义式和牛顿力学可以证明：太阳和太阳系的行星都是绕太阳系质心运动的。
第二节、“M-Mg质心”概念的定义和它的运动性质。（5～7页）
内容提要：本节从理论上定义了“M-Mg质心”这一概念，并在理论上对它的运动性质进行了一定的分析和论述。
应该指出的是：如果我们在理论分析中可以忽略不同行星之间的相互影响，那么我们就可以利用“一个行星和太阳两者绕太阳系质心运动”的简单模型，来分析行星的运动规律。
然而，如果我们在理论分析中需要考虑到不同行星之间的相互影响时，那么我们就应该用“M-Mg质心”取代太阳质心，来分析行星的运动规律。
第三节、行星在近日点和远日点绕太阳系质心运动的性质和特点。（7～9页）
内容提要：本节从理论上对行星近日点和远日点绕太阳系质心运动的四个特性展开了分析证明。
第四节、行星绕太阳（或M-Mg质心）运动的轨道不是椭圆曲线。（9～12页）
内容提要：本节利用行星近日点和远日点的四个运动特性，从理论上分析证明了：开普勒行星运动轨道定律是一个错误的定律，即行星绕太阳运动的轨道不是椭圆曲线。
第五节、牛顿万有引力定律与“能量守恒定律”是互相矛盾的。（12～15页）
内容提要：本节从太阳系质心参照系的角度，根据牛顿力学、动量守恒定理，在理论上分析证明了：“牛顿万有引力定律”与“能量守恒定律”是互相矛盾的。
第六节、新的万有引力公式的推导。（15～19页）
内容提要：本节从太阳系质心参照系的角度，根据牛顿力学、向心力公式、角动量守恒定理，在理论上分析推导出了新的万有引力定律的数学表达式，即本文中的第（11）关系式。
第七节、开普勒“行星运动面积相等定律”与“角动量守恒定理”是互相矛盾的。（19～23页）
内容提要：本节从太阳系质心参照系的角度，利用牛顿力学、角动量守恒定理，在理论上分析证明了：开普勒“行星运动面积相等定律”与“角能量守恒定理”是互相矛盾的。
第八节、行星绕太阳（或M-Mg质心）运动的周期。（23～24页）
内容提要：本节从太阳系质心参照系的角度，根据新的万有引力公式推导出了行星绕太阳运动的“新的周期定律”。
第九节、行星绕太阳（或M-Mg质心）运动轨道应该满足的约束条件。（24～27页）
内容提要：本节通过严谨﹑慎密的逻辑推理和理论分析，提出了行星绕太阳系质心运动应该满足的一组方程式。
文章序言
序言一、我通过理论分析和逻辑推理发现并建立了一个全新的行星运动理论。
哥白尼的“日心说”运动模型与恒星系绕“恒星系质心”的实际运动，两者之间的误差是较大的。
为了修正哥白尼“日心说运动模型”的这一重大的理论缺陷，本文根据质点系统质心的定义式和牛顿力学，在理论上提出了“太阳系质心说”（或“恒星系质心说”）运动模型即：“太阳系质心”位于太阳系的中心静止不动，而太阳和太阳系的行星都是绕太阳系质心运动的。由此我发现和创立了一个全新的行星运动理论。
本文通过严密的理论分析研究后发现：如果利用“太阳系质心说”运动模型，来分析说明行星和太阳的运动，那么我们在理论上就可以对“日心说”运动模型一直无法分析解释的许多理论难题，做出合理科学的解释。从理论与实际应该相符合的科学标准来讲，“太阳系质心说”运动模型要比“日心说”运动模型更合理，更科学。
序言二、新的行星运动理论是建立在下面四个基石之上的。
基石（一）、行星和太阳无论在何时、在何处都是绕太阳系质心运动的。
基石（二）、太阳系质心参照系是一个惯性系。
基石（三）、“M-Mg质心”概念的定义和它的运动性质。
基石（四）、所有的行星在近日点（或在远日点）绕太阳系质心的运动都具有的四个共性。（详细的分析证明，请看论文的第三节。）
特性（1）。所有的行星在近日点（或在远日点）都是绕太阳系质心运动的。
特性（2）。所有的行星在近日点（或在远日点）绕太阳系质心运动的速度V的方向，与行星质心到太阳系质心的连线都是互相垂直的。
特性（3）。所有的行星在近日点（或在远日点）的加速度a都是指向太阳系质心的。
特性（4）。根据曲率概念的定义，通过理论分析可以证明：所有的行星在近日点（或在远日点）运动的曲率中心都是太阳系质心。
序言三、本文分析研究“万有引力定律”的起点,比牛顿分析研究的起点更简单、更合理、更科学。
任何一种理论学说一般都是利用某一个观测事实做起点建立起来的。例如：相对论是利用光速不变的观察结果做起点建立起来的。
我们知道，开普勒“行星运动周期定律”是利用天文学家第谷教授的天文观测结果做起点建立起来的。由于第谷教授进行天文观测的设备太原始、太落后，因此在他的天文观测结果中可能存在着一定的观测误差。又因为隐藏在第谷教授天文观测结果中的数学关系式太复杂，从而使得开普勒花费了九年的时间才分析归纳出了他的“行星运动周期定律”（本人通过理论分析发现：该定律是错误的）。从这两点来讲，开普勒利用第谷教授天文观测结果所分析归纳出来的“行星运动周期定律”与行星绕太阳的实际运动可能存在着一定的人工误差。
既然牛顿万有引力定律是利用开普勒“行星运动的周期定律”做起点建立起来的，那么牛顿分析研究万有引力定律的起点，就不属于对客观事实直接的观测结果，而是属于可能包含有人工误差的观察定律。
然而我的新理论学说的起点，与牛顿分析研究引力定律的起点是不同的。本文分析研究新万有引力定律的起点，属于对客观事实直接的、正确的观测结果即：“行星在近日点绕太阳运动的速度最大，到太阳的距离最小，而行星在远日点绕太阳运动的速度最小，到太阳的距离最大”。例如，人造卫星绕地球的运动。由此可以确定：我分析研究“万有引力定律”的起点,比牛顿分析研究的起点更简单、更合理、更科学。
综上所述，我发现新万有引力定律的过程是：
太阳系质心运动模型——行星近日点和远日点的四个运动特性——向心力公式和角动量守恒定理——新的万有引力定律。
而牛顿发现万有引力定律的过程是：
哥白尼日心说运动模型——第谷教授的天文观测结果——开普勒行星运动周期定律——牛顿万有引力定律。
行星绕太阳系质心运动的规律，与行星绕太阳运动的规律，应该是同一个行星运动规律，在两个不同参照系中的不同表现形式而已。从这一点来讲，行星在太阳系质心参照系中的运动规律，与行星在太阳参照系中的运动规律，两者在理论上应该是可以进行等效转换的。一种能够正确说明行星运动规律的理论，就应该能够在太阳系质心参照系和太阳参照系两者中进行相等的理论转换。否则它就是一种错误的理论学说。
由于牛顿万有引力定律和开普勒行星运动三大定律，都无法在“太阳系质心参照系”和太阳参照系两者中进行相等的理论转换，因此牛顿万有引力定律和开普勒行星运动三大定律都是错误的学说。
第一节、太阳和太阳系的行星都是绕太阳系质心运动的。
假设在太阳系中包含着N个天体（即太阳和太阳系行星的数量之和）。如果用太阳系质心做参照系的原点，那么根据质点系统质心的定义式，我们可以得到下面的关系式。
上式中的Mg是第g个星体质点（即行星或太阳）的质量，式中的Rg是第g个星体质点（即行星或太阳）到太阳系质心的距离。把上式对时间微分后，根据牛顿力学可以证明：太阳系中的质点（即太阳和太阳系的行星）都是绕太阳系质心运动的。
由于哥白尼的“日心说”运动模型认为：太阳系的行星都是绕太阳运动的，因此人们在理论上则无法对“太阳和太阳系的行星为什么不是绕太阳系质心运动”这一问题做出合理科学的解释。
从理论上讲，牛顿和开普勒都是从太阳质心这一角度来分析研究行星运动的。而本文则是从太阳系质心这一角度来分析研究行星运动的。
人们从不同的角度，观察同一个事物会得到不同的结论。例如：对于平面内的圆曲线来讲，如果在平面内观察它，那末它就是一条直线，如果在平面和圆曲线的外侧观察它，那末它就是一条椭圆曲线，如果在平面和圆曲线的正上方俯视它，那末它才是一条圆曲线。
同样的道理，由于太阳系中所有的质点都是绕太阳系质心运动的，而不是绕太阳运动的，因此从理论上讲，本文分析研究行星运动的角度，比牛顿和开普勒两者分析研究行星运动的角度更合理，更科学。
第二节、“M-Mg质心”的定义和它的运动性质
为了简化理论分析推导，本文把太阳系质点系统所有的质点，在理论上重新进行了组合简化。使重新组合简化后的“新太阳系质点系统”中只包含着两个质点粒子。其中的一个质点粒子是第g个行星的质心，而另一个质点粒子是太阳质量与其它行星质量所组成的质心。假设太阳系的总质量为M，假设行星g的质量为Mg。本文把质量（M-Mg）所组成的质心定义为：第g个行星的“M-Mg质心”。
需要指出的是：每一个行星都对应着一个“M-Mg质心”，不同的行星所对应的“M-Mg质心”是不同的。根据质点系统质心的定义式可以确定：第g个行星以及它所对应的“M-Mg质心”都是绕太阳系质心运动的。
从理论上讲，“M-Mg质心”与太阳系质心是两个不同的质心点。由于太阳系质量M仅仅比“质量（M-Mg）大了行星g的质量Mg，因此“M-Mg质心”与太阳系质心两者之间的距离是非常微小的。显然行星g的质量Mg越大（或者越小），那么“M-Mg质心”与太阳系质心两者之间的距离就越大（或者越小）。
同样，“M-Mg质心”与太阳质心也是两个不同的质心点。然而在太阳系中，由于太阳的质量远远大于太阳系行星质量的总和，而且太阳系的行星也不是排列在一条直线上绕太阳运动，因此“M-Mg质心”与太阳质心两者之间的距离也是非常微小的。
当我们在太阳质心上观测行星的运动时。那么太阳是静止不动的，而行星都是绕太阳运动的。同样，当我们在“M-Mg质心”上观测行星g的运动时。那么“M-Mg质心”是静止不动的，而行星g则是绕“M-Mg质心”运动的。由于“M-Mg质心”是太阳和其它行星在理论上所组成的质心，因此太阳质心和“M-Mg质心”两者绕太阳系质心运动的性质是完全相同的。
影响太阳和行星绕太阳系质心运动的因素虽然很多，但不同行星之间的影响力是较小的，而太阳对行星的影响力是很大的。
如果我们在理论分析中可以忽略不同行星之间的影响时，那么我们就可以用行星g和太阳两者绕太阳系质心运动的简单模型，来分析行星的运动规律。
相反，如果我们在理论分析中需要考虑到其它行星对第g个行星绕太阳系质心运动的影响时，那么我们就应该用行星g和“M-Mg质心”绕太阳系质心运动的复杂模型，来分析行星的运动规律。
由于太阳质心和“M-Mg质心”两者绕太阳系质心运动的性质完全相同，因此行星g和太阳两者绕太阳系质心运动的简单模型，与行星g和“M-Mg质心”两者绕太阳系质心运动的复杂模型，在结构和性质上也是完全相同的。
此外，由于太阳质心与“M-Mg质心”两者之间的距离非常小，因此行星g绕太阳运动的方式，与行星g绕“M-Mg质心”运动的方式也是完全相同的。由此可以确定：行星g绕太阳运动的近日点，应该对应着行星g绕“M-Mg质心”运动的近“M-Mg质心”点（该点是行星距离“M-Mg质心”最近的轨道点）。而行星绕太阳运动的远日点，则应该对应着行星绕“M-Mg质心”运动的远“M-Mg质心”点（该点是行星距离“M-Mg质心”最远的轨道点）。
同样，行星绕太阳运动所具有的距离﹑速度﹑动量﹑引力势能﹑角动量和万有引力等运动变量，则应该对应着行星绕“M-Mg质心”运动所具有的距离﹑速度﹑动量﹑引力势能﹑角动量和万有引力等运动变量。
由于太阳和第g个行星绕太阳系质心运动的简单模型，与“M-Mg质心”和行星g绕太阳系质心运动的复杂模型，在运动性质和运动变量上是完全相同的，因此本文所定义的“M-Mg质心”概念，相当于太阳质心这个概念。由此可以确定：天文学家对行星绕太阳运动规律的分析和论述，在理论上也可以看成（或者相当于）是对行星绕“M-Mg质心”运动规律的分析和论述。
由于“M-Mg质心”质心概念相当于太阳质心概念，因此本文下面对行星绕太阳运动规律的分析和论述，实质上也是对行星绕“M-Mg质心”运动规律的分析和论述。
特别应该指出的是：为了简化理论分析和推导，本文在下面分析推导中所使用的近日点和远日点两个概念具有两方面的含意。对于简单模型中的太阳来讲，近日点和远日点两个概念的含意不变。但是对于复杂模型中的“M-Mg质心”来讲，近日点的含意是指近“M-Mg质心”点，而远日点的含意是指远“M-Mg质心”点。
第三节、所有的行星在近日点（或在远日点）绕太阳系质心运动的共性
假定行星g的质量是Mg，假定太阳系的质量是M。假定行星质心到太阳（或到M-Mg质心）线段上的H点是太阳系质心，（本文下面把太阳系质心简称为“质心H”）。
由于可以把太阳系质心参照系看成是“惯性系”，因此我们在理论上就可以假定：所有外部力量作用在质心H上的矢量之和恒等于零。当我们利用质心H做太阳系参照系的原点时。那么不论行星到太阳(M-Mg质心)的距离是增大还是缩小，太阳系质心参照系的运动状态始终不发生变化。
当我们在太阳系质心参照系中观测行星和太阳（或M-Mg质心）两者的运动时，此时假定行星质心到质心H的距离是RH。假定行星绕质心H运动的切向速度是VH，加速度是aH。当行星在近日点（或者在远日点）绕质心H运动时，此时行星绕质心H的运动就具有下面四个特性。
特性（1）。由于行星和太阳无论在何时、在何处都是绕质心H运动的，因此所有的行星在近日点和远日点两个位置上都是绕质心H运动的。
特性（2）。所有的行星在近日点（或在远日点）绕质心H运动的切向速度VH，与行星质心到质心H的线段都是互相垂直的。
行星绕质心H运动的切向速度VH，可以分解成为两个方向互相垂直的速度分量。其中一个是横向速度VHX。它的速度方向与行星质心到质心H的线段RH是互相垂直的。另外一个是径向速度VHR。它的速度方向是从行星质心指向质心H的。切向速度VH、速度分量VHX和VHR，它们三者之间的变化关系是：
从数学微分的角度讲，由于行星质心到质心H的距离RH，在近日点前后位置上的变化方向是相反的。（或者距离RH在远日点前后位置上的变化方向是相反的），——即在近日点前面位置上的距离RH
，是逐渐缩小的（或者是逐渐增大的）。而在近日点后面位置上的距离RH
，是逐渐增大的（或者是逐渐缩小的）——，因此行星在近日点绕质心H运动的径向速度
,（或者在远日点绕质心H运动的径向速度
)。于是行星在近日点绕质心H运动的切向速度VH，与行星质心到质心H的线段是互相垂直的。（或者行星在远日点的切向速度VH，与行星质心到质心H的线段是互相垂直的）。
特性（3）。所有的行星在近日点（或在远日点）加速度aH的方向都是指向质心H的。
行星绕质心H运动的加速度aH，可以分解成为两个不同方向的加速度。其中一个是切向加速度
。另外一个是从行星质心指向质心H的法向加速度aHR。
当行星绕质心H运动时。由于切向速度VH在近日点前后位置上的变化方向是相反的。（或者切向速度VH在远日点前后位置上的变化方向是相反的）。——即在近日点前面位置上的切向速度VH
，是逐渐增大的（或者是逐渐缩小的）。在近日点后面位置上的切向速度VH
，是逐渐缩小的（或者是逐渐增大的）——。因此行星在近日点（或者在远日点）的切向加速度
。于是行星在近日点的加速度aH的方向是指向质心H的。（或者行星在远日点的加速度aH的方向是指向质心H的。）
特性（4）。所有的行星在近日点（或在远日点）运动的曲率中心都是太阳系质心。
对于（空间的）近日点（或远日点）来讲，取它前后两个邻近点Q和R，过这三点作一个圆。当Q、R沿轨道曲线接近近日点（或接近远日点）时，由于行星在近日点（或在远日点）是绕太阳系质心运动的，因此这个圆的极限位置就是以行星近日点（或远日点）到太阳系质心距离为半径的圆（是过近日点和太阳系质心两点无数圆的最小半径圆）。由此可以确定：以行星近日点（或远日点）到太阳系质心距离为半径的圆，就是行星绕太阳系质心运动的轨道曲线在近日点（或远日点）的曲率圆。
根据上面的分析可以得到结论：在太阳系质心参照系范围内，所有的行星在近日点（或在远日点）运动的曲率中心就是太阳系质心。
于是所有行星近日点的曲率等于近日点到太阳系质心距离的倒数。而所有行星远日点的曲率等于远日点到太阳系质心距离的倒数。
我们利用同样的分析方法可以证明：当太阳（或M-Mg质心）到行星的距离变化到最小值(或者变化到最大值)时，此时太阳（或M-Mg质心）绕质心H的运动也同样具有上面的四个运动特性。
根据特性（4）我们可以直接推导出一个结论即：行星绕太阳系质心运动的轨道不是椭圆轨道。
假定行星近日点到质心H的距离是RH1。假定行星远日点到质心H的距离是RH2。由于质心H是近日点和远日点两者的曲率中心，因此行星绕质心H运动的近日点曲率半径RH1，比行星绕质心H运动的远日点曲率半径RH2小（即RH1＜RH2）。于是行星绕质心H运动的轨道，就是一个近日点曲率半径RH1比远日点曲率半径RH2小的曲线。该曲线类似于鸡蛋壳长轴的剖面曲线。本文把该曲线称为“蛋圆曲线”，把行星绕质心H运动的轨道称为“行星蛋圆曲线轨道”，把太阳（或M-Mg质心）绕质心H运动的轨道称为“太阳蛋圆曲线轨道”。
我在《数学手册》中没有找到数学家们关于“蛋圆曲线”的定义和论述。对于行星绕太阳系质心运动来讲，本文所称为的“蛋圆曲线”在数学上应该具有以下几个性质。
[1]﹑本文所称为的“蛋圆曲线”在数学上只具有一个焦点。本文把该焦点称为“蛋圆曲线焦点”。太阳系质心则位于该焦点上。
[2]﹑“蛋圆曲线”没有短轴，只有长轴。
[3]﹑“蛋圆曲线”是以长轴为对称轴的曲线。
[4]﹑“蛋圆曲线”长轴两端点的曲率是不相等的。
[5]﹑“蛋圆曲线”长轴每一个端点的曲率半径等于该端点到“蛋圆曲线焦点”（即到太阳系质心）的距离。
[6]﹑“蛋圆曲线”上的每一点都对应着一条椭圆曲线。不对称的“蛋圆曲线点”对应着不同的椭圆曲线。
[7]﹑“蛋圆曲线”上的每一点所对应的椭圆曲线的离心率都是相等的
[8]﹑“蛋壳曲线”具有一个焦点参数P，该焦点参数P是一个变量，或者说焦点参数P是极角θ的函数。即
P＝f(θ)。
第四节、行星绕太阳（或M-Mg质心）运动的轨道不是椭圆曲线。
当我们在太阳（或M-Mg质心）参照系内观测行星的运动时，根据开普勒“行星运动轨道定律”，假设行星绕太阳（或M-Mg质心）运动的椭圆轨道极坐标公式等于下面的关系式。
由上式可知，行星椭圆轨道近日点和远日点的曲率半径是相等的，即都等于椭圆轨道的焦点参数
。式中的a为椭圆的长半轴，而b则为椭圆的短半轴，
当我们根据太阳质心（或M-Mg质心）参照系，来确定行星近日点和远日点的曲率中心时。假定行星近日点到太阳（或M-Mg质心）的距离是R1。此时由于极角
，因此得到关系式
。该关系式表明：行星近日点的曲率半径P大于近日点到太阳（或M-Mg质心）的距离R1。由于，，因此近日点绕太阳（或M-Mg质心）运动的曲率中心位于行星与太阳（或M-Mg质心）的连线之外。
同理，假定行星远日点到太阳（或M-Mg质心）的距离是R2。此时由于极角θ=
，因此得到关系式R2＞
。该关系式表明：行星远日点的曲率半径P小于远日点到太阳（或M-Mg质心）的距离R2。由于R2＞，因此远日点绕太阳（或M-Mg质心）运动的曲率中心位于行星与太阳（或M-Mg质心）的连线之内。
当我们根据太阳系质心参照系来确定行星近日点和远日点的曲率中心时，那么行星近日点和远日点的曲率中心都是太阳系质心。然而，当我们根据普勒行星运动轨道定律来确定行星近日点和远日点的曲率中心时，那么行星近日点和远日点绕太阳（或M-Mg质心）运动的曲率中心，一个位于行星与太阳（或M-Mg质心）的连线之外，而另一个则位于行星与太阳（或M-Mg质心）的连线之内。由此我们可以确定：开普勒行星运动轨道定律与行星绕太阳系质心运动的事实是互相矛盾的。
此外，我们通过理论分析可以证明：行星绕太阳（或M-Mg质心）运动的轨道不是椭圆曲线。下面我们分析讨论一下这个问题。
当我们在质心H参照系内观测行星的运动时，根据曲线运动的规律可以得到下面两个结论：
结论（1）。行星在近日点绕质心H运动的曲率半径
，与行星此时到质心H的距离RH1相等（即 ρ＝RH1≠
）。行星在远日点绕质心H运动的曲率半径ρ2，与行星此时到质心H的距离RH2相等（即
ρ2＝RH2≠
）。
结论（2）。当行星在近日点（或远日点）绕质心H运动时，行星此时受到的向心力F与行星和太阳（或M-Mg质心）两者之间的万有引力相等。
根据同样的理由。当太阳（或M-Mg质心）在距离行星最近的点绕质心H运动时，或者当太阳（或M-Mg质心）在距离行星最远的点绕质心H运动时，太阳（或M-Mg质心）此时绕质心H的运动同样符合上面两个结论。
当我们利用质心H做参照系原点时。此时假定行星在近日点绕质心H运动的切向速度是VH1。假定行星在近日点到质心H的距离是RH1。同时假定太阳（或M-Mg质心）在近日点时刻绕质心H运动的切向速度是VS1。假定太阳（或M-Mg质心）在近日点时刻到质心H的距离是RS1。于是行星在近日点到太阳（或M-Mg质心）的距离R1＝RH1-RS1。
由于行星切向速度VH1和太阳（或M-Mg质心）切向速度VS1两者的方向，垂直于行星质心到太阳（或M-Mg质心）的距离R1，因此行星在近日点绕太阳（或M-Mg质心）运动的切向速度V1＝VH1-VS1。当行星在近日点绕质心H运动时。此时利用质点系统质心的定义和“动量守恒定律”可以得到下面四个关系式。
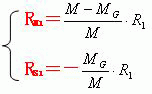
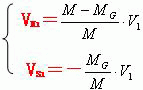(1)
当我们在质心H参照系内，观测行星和太阳（或M-Mg质心）两者的运动时。根据行星近日点的四个运动特性，利用向心加速度公式可以证明：行星和太阳（或M-Mg质心）两者在近日点时刻受到的向心力（即指向质心H的向心力）F1和-F1分别等于下面的关系式：
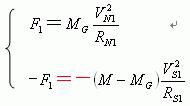(2)
把关系式（1）代入到关系式（2）中，可以得到下面的关系式（3）。
由于行星在近日点绕太阳（或M-Mg质心）运动的切向速度V1，属于太阳（或M-Mg质心）参照系中的变量，而行星质心到太阳（或M-Mg质心）的距离R1也属于太阳（或M-Mg质心）参照系中的变量，因此当我们在太阳（或M-Mg质心）参照系内，观测行星和太阳（或M-Mg质心）两者的运动时。此时行星和太阳（或M-Mg质心）两者在近日点时刻所受到的向心力（即指向质心H的向心力）F1和-F1分别等于下面的关系式：
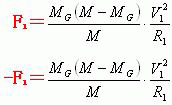(3)
在太阳（或M-Mg质心）参照系内，根据质点曲线运动的性质和关系式（3），我们可以得到行星在近日点绕太阳（或M-Mg质心）运动的曲率半径 ρ1即：
假定行星质心在远日点到太阳（或M-Mg质心）的距离是R2。我们根据同样的理由可以得到行星在远日点绕太阳（或M-Mg质心）运动的曲率半径ρ2 即：
由于距离R2＞距离R1，因此曲率半径 ρ2 ＞曲率半径ρ1 。上面的分析结果说明：在太阳参照系中，行星绕太阳运动的轨道不是椭圆曲线，而是一个“蛋圆曲线”。
我们根据前面分析讨论的结果可以确定：在太阳（或M-Mg质心）参照系内，当远日点的曲率半径 ρ2 比行星到太阳（或M-Mg质心）的距离R2大时（即曲率半径 ρ2＞距离R2），此时行星绕太阳（或M-Mg质心）的运动，可以变换到行星绕质心H的运动。
由于开普勒行星运动轨道定律与行星在近日点和远日点绕质心H运动的规律是互相矛盾的，而且开普勒行星运动轨道定律也不能在太阳（或M-Mg质心）参照系和太阳系质心参照系两者内，进行相等的理论变换，因此它是一个错误的理论学说。
第五节、“牛顿万有引力定律”与“能量守恒定律”是互相矛盾的。
当我们在太阳（或M-Mg质心）参照系内观测行星运动时，假定行星和太阳（或M-Mg质心）两者在近日点时刻，所具有的动能和引力势能之和是ES1。假定行星和太阳（或M-Mg质心）两者在远日点时刻，所具有的动能和引力势能之和是ES2。根据牛顿力学可以得到下面两个关系式。
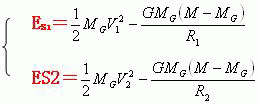
上面两个关系式内的字符G是万有引力常数。利用“能量守恒定律”可以得到关系式ES1＝ES2 即。
(4)
根据开普勒“行星运动轨道定律”，假定行星椭圆轨道长轴两个端点的曲率半径是ρ 。利用椭圆曲线的性质可以得到下面的关系式。
利用牛顿万有引力定律﹑向心加速度公式和开普勒“行星运动轨道定律“可以得到下面两个关系式。
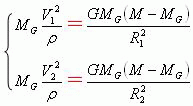即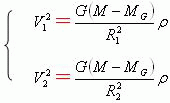 
把上面的关系式代入到关系式（4）中，可以得到下面的关系式。
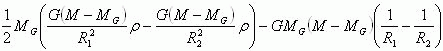
上面的理论分析结果表明：如果行星绕太阳（或M-Mg质心）运动的轨道是椭圆轨道，那么在太阳（或M-Mg质心）参照系内，牛顿万有引力定律完全符合“能量守恒定理”的要求。然而在上面的理论分析推导结果中却包含着两个致命的理论错误。
首先根据前面分析讨论的结果我们已经知道。开普勒行星运动轨道定律是一个错误的理论学说。即行星绕太阳（或M-Mg质心）运动的轨道不是椭圆曲线，而是一个蛋圆曲线。
其次在上面的分析结果中，隐藏着“太阳（或M-Mg质心）绕质心H运动的速度始终不发生变化”这个条件。该条件显然不符合太阳（或M-Mg质心）绕质心H的运动。由于太阳绕太阳系质心运动的速度会发生变化，因此太阳参照系在太阳系质心参照系中就不是一个严格的惯性系。
当我们在太阳（或M-Mg质心）参照系内观察太阳（或M-Mg质心）和行星两者的总动量时，太阳（或M-Mg质心）的动量始终是等于零的。由于行星近日点所对应的太阳（或M-Mg质心）速度（即太阳此时绕太阳系质心运动的速度），与行星远日点所对应的太阳（或M-Mg质心）速度（即太阳此时绕太阳系质心运动的速度）不相等，因此行星和太阳（或M-Mg质心）两者在近日点时刻所具有的动能和引力势能之和，与两者在远日点时刻所具有的动能和引力势能之和是不相等的。从这一点来讲，在太阳（或M-Mg质心）参照系内不能直接利用“能量守恒定理”（即总机械能守恒定律），来分析讨论行星绕太阳（或M-Mg质心）运动的规律。
由于太阳系质心参照系是一个惯性系，而太阳和太阳系的行星都是绕太阳系质心运动的，不是绕太阳运动的，因此只有“太阳和行星绕太阳系质心运动”的轨道动能与引力势能两者的总和，才是理论上唯一有资格符合“能量守恒原理”要求的物理量即：太阳和太阳系行星绕太阳系质心运动所具有的轨道动能与引力势能的总和是一个保持不变的常量。
应该指出的是：由于太阳在太阳参照系中的运动速度恒等于零，而太阳相对于太阳系质心来讲具有一定的轨道动能，因此行星绕太阳运动的轨道动能总和，在理论上必然不符合“能量守恒定理”的要求即：行星绕太阳运动的轨道动能与引力势能的总和不是一个常量。
下面我们通过理论分析再证明一下上面的结论。
在质心H参照系内，假定行星和太阳（或M-Mg质心）两者在近日点时刻，所具有的动能和引力势能之和是EH1。那末EH1则等于下面的关系式。
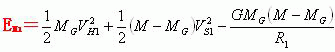
把关系式（1）代入到上面的关系式中，可以得到下面的关系式
假定行星和太阳（或M-Mg质心）两者在远日点时刻，所具有的动能和引力势能之和是EH2。那末根据上面同样的理由，EH2等于下面的关系式。
根据“能量守恒定律”可以确定:EH1＝EH2。由此可以得到下面的关系式。
(5)
当行星在近日点和远日点两个位置绕质心H运动时。此时利用关系式（3）和牛顿万有引力定律可以得到下面两个关系式。
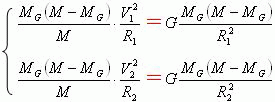即 
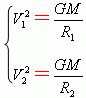(6)
把上面的关系式代入到关系式（5）中，可以得到下面的关系式。
上面的分析结果表明：在质心H参照系内，牛顿万有引力定律与“能量守恒定理”是互相矛盾的。此外,上面的分析结果使得人们无法从理论上说明两个问题。
首先无法从理论上说明：“太阳系的总能量为什么是负能量”这个问题。假定在太阳系统中只包含太阳和一个行星，该系统的总能量应该等于太阳和行星两者总动能与引力势能之和。在太阳参照系中利用牛顿力学通过计算可以确定：太阳系统的总能量等于行星在某一轨道点上的引力势能（即等于上面的分析推导结果）。
引力势能是一种负能量，它的物理学含意是把行星从相对于太阳系质心无限远处移动到该轨道点处外力所做的功。既然太阳系统的总能量是负的能量，那么则说明有某一种外力对太阳系统做了功，即把太阳系统从无限远处移动到了现在的位置。虽然太阳系统是绕银河系中心运动的，但太阳系统绕银河系中心运动的引力势能绝对不等于行星绕太阳运动的引力势能。那么究竟是谁，或者是那一种外力对太阳系做了功呢？而太阳系统的负引力势能又是相对于哪一个参照系计算出的呢？很显然，利用牛顿和开普勒的理论是无法解释这个问题的。
其次无法从理论上说明：“用太阳做参照系的原点时，太阳系的总能量为什么不恒等于零。”
从理论上讲，我们可以把太阳系的全部质量看成是集中在太阳系质心上。当我们用太阳系质心做参照系原点时，由于太阳系的全部质量是集中在太阳系质心上，因此太阳系的总质量相对于太阳系质心原点的运动速度是恒等于零的。又由于太阳系的总质量相对于太阳系质心原点来讲不存在着任何引力势能，因此根据牛顿力学可以确定：太阳系的总能量相对于太阳系质心参照系来讲应该是恒等于零的。
第六节、新“万有引力公式”的推导。
假定行星质心到质心H的距离是RH。假定太阳质心（或M-Mg质心）到质心H的距离是RS。根据质点系统质心的定义式，我们可以得到关系式：MGRH+MSRS＝0。因为行星质心到太阳（或M-Mg质心）的距离R＝RH-RS。于是我们可以得到下面两个关系式。
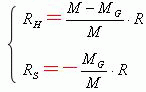（7）
把上面的关系式对时间t进行微分后，可以得到下面两个关系式。
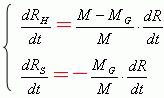（8）
对于行星和太阳两者的角动量来说：由于行星和太阳两者在绕质心H运动的同时，还分别绕自转轴进行自转运动，因此行星和太阳（或M-Mg质心）都具有两种类型的角动量。一种是绕质心H运动的轨道角动量，另一种是绕自转轴运动的自转角动量。
由于行星（或者太阳）在运动轨道上每一点的自转速度都是相等的，而行星（或者太阳）在近日点到远日点之间绕质心H运动的速度却是不相等的，因此行星（或者太阳）自转运动的角速度，与行星（或者太阳）绕质心H运动的角速度是互相独立运动的，即两者之间不存在任何函数变化关系。由此我们可以确定：行星（或者太阳）的自转角动量，与行星（或者太阳）的轨道角动量之间不存在任何函数变化关系。
在质心H参照系内，假定行星和太阳（或M-Mg质心）两者绕质心H运动的角速度是
。假定行星绕质心H运动的轨道角动量是LG。假定太阳（或M-Mg质心）绕质心H运动的轨道角动量是LS。根据质点系统角动量的定义，可以得到下面两个关系式。
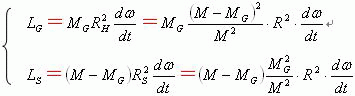
由于太阳系质心参照系是一个惯性系，因此各种外力和内力在质心H上的力矩矢量总和恒等于零。根据“角动量守恒定理”可以确定：太阳系绕质心H运动的轨道角动量总和是一个常量。假定该常量 L＝Lg+Ls。于是我们可以得到下面的关系式。
（9）
上式中的角速度（dω/dt）是行星g绕太阳系质心运动的角速度。不是行星g绕太阳运动的角速度。由于行星和太阳（或M-Mg质心）两者绕太阳系质心运动的角动量之和 L 属于太阳系统的总角动量，因此上式对于太阳系中的每一个行星都是成立的。
从数学关系式上讲，关系式（9）与开普勒“行星运动面积相等定律”是非常相似的。但是开普勒“行星运动面积相等定律”中的角速度是行星绕太阳（或M-Mg质心）运动的角速度，不是行星绕太阳系质心运动的角速度。
需要指出的是：行星和太阳（或M-Mg质心）两者绕质心H运动的角速度
，与行星绕太阳（或M-Mg质心）运动的角速度
，是两个不同参照系中的角速度。由于角速度，是在质心H参照系内发生变化，不是在太阳（或M-Mg质心）参照系内发生变化，因此在太阳（或M-Mg质心）参照系内，我们不能直接利用关系式（9）来分析讨论行星的运动规律。
把关系式（7）代入关系式（9）后可以得到下面的关系式。
对于太阳系来讲，上式中的Mg﹑RH和三者的变化是互相制约的。
假定行星在近日点时刻绕质心H运动的速度是VH1，在远日点时刻绕质心H运动的速度是VH2。假定太阳（或M-Mg质心）在近日点时刻绕质心H运动的速度是VS1，在远日点时刻绕质心H运动的速度是VS2。由于速度VH1和速度VS1两者的方向相反 ，（或者速度VH２和速度VS２两者的方向相反），因此行星在近日点绕太阳（或M-Mg质心）运动的速度V1＝VH1-VS1。而行星在远日点绕太阳（或M-Mg质心）运动的速度V2＝VH2-VS2。
由于行星和太阳（或M-Mg质心）两者在近日点时刻（或者在远日点时刻），绕质心H的运动必需满足关系式（9）。因此我们可以得到下面的关系式。
（10）
上式中的R1与V1分别是近日点的距离和速度，而R2与V2则分别是近日点的距离和速度。由于关系式（9）对于太阳系中所有的行星都是成立的，因此上式对于太阳系中所有的行星也都是成立的。
由于关系式（6）是我们利用牛顿万有引力定律得到的。把上面的关系式代入到关系式（6）中，我们可以得到下面关系式。
在客观实际中，行星在近日点绕太阳（或M-Mg质心）运动的切向速度V1， 与行星在远日点绕太阳（或M-Mg质心）运动的切向速度V2是不相等的即：V1≠V2。由此我们可以确定：牛顿万有引力定律与“角动量守恒定律”是互相矛盾的。
把关系式（10）代入到关系式（3）中，我们可以得到下面两个关系式。
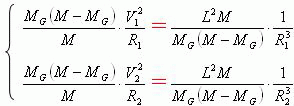
对于上面的两个关系式来讲，等号左边的两个关系式分别是：行星在近日点和远日点两个位置上绕质心H运动的向心力关系式。然而在等号右边的两个关系式内，单独对于一个行星来讲，只有距离R是一个变量，其它的量都是常量。当行星在近日点位置时，（或者当行星在远日点位置时），由于行星此时受到的向心力与行星和太阳（或M-Mg质心）两者之间的万有引力相等，因此等号右边的两个关系式，只能是行星和太阳（或M-Mg质心）两者之间的万有引力关系式。
由于上式对于所有的行星指向太阳系质心的引力都是成立的，因此上式中行星质量Mg就属于变量。又因为式中的常数 M 和 L 只是太阳系的质量和所有星体角动量的总和，而不同的恒星系所具有的质量和角动量总和是不相同的。因此常数项L2M 就不是自然界中的引力常数G。然而在自然界中引力常数对于任何一个恒星系中的物体来讲都应该是相同的。从这一点讲，在常数项L2M 中就包含着自然界中的引力常数G。
对于关系式（10）来讲。角动量 L 中包含着质量Mg、距离R和速度V这三个变量，但是角动量 L 的大小与三者的变化无关。只有当太阳系的质量M发生变化时，角动量 L 的大小才会发生变化。从物理量纲上分析，角动量 L 的大小与质量M的一次方成反比。基于这一点，可以确定宇宙中的引力常数G＝L/M。
由于宇宙中的引力常数G＝L/M，因此上式行星和太阳（或M-Mg质心）两者之间的万有引力关系式可以写成下面的形式即：
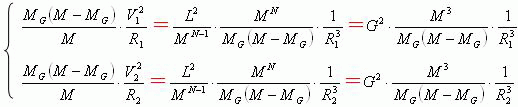
上式等号左边的两个关系式就是自然界中任何两个星体之间的万有引力公式，由此我们可以得到新的万有引力公式即：
即：
(11)
上式就是适合于所有物体的万有引力公式。式中的M1和M2是两个物体的质量。
公式（11）表明：两个物体之间引力的大小，与两个物体质量之和的立方成正比。与两个物体质量乘积成反比。与两个物体之间距离R的立方成反比。
利用关系式（11）可以确定出行星绕质心H运动的向心力FH。即：
而太阳绕质心H运动的向心力-FH。为：
根据牛顿万有引力定律，行星和太阳之间的万有引力的大小是：
如果欲使牛顿万有引力的数值等于新万有引力的数值，那么牛顿万有引力定律中的引力常数G就应该等于下面的关系式。
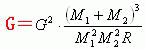
上式中的变量R是行星到太阳的距离。由上式可以确定：引力常数G在“牛顿万有引力定律”中不是一个保持不变的常数。而是一个变量。具体地讲，在同一地点，当人们到地球中心的距离不断缩小时，此时牛顿万有引力定律中的“引力常数G”是不断增大的。当人们到地球中心的距离不断增大时，此时牛顿万有引力定律中的“引力常数G”是不断变小的。从这一点来讲，“牛顿万有引力定律”中的“引力常数G”与自然界中的引力常数是两个不同的事物。或者说：牛顿万有引力定律中的“引力常数G”此时已经是“名存实亡”了。从这一点讲，学术界目前对“引力常数G”的分析和讨论是毫无意义的。
我们利用关系式（11）可以得到新的引力势能公式即。
(12)
第七节、开普勒“行星运动面积相等定律”与“角动量守恒定理”是矛盾的。
当我们在太阳系质心参照系中观测行星的运动时，那末太阳和太阳系的每一个行星都具有一个绕太阳系质心运动的角速度。需要指出的是：行星绕太阳系质心运动的角速度，与行星绕太阳运动的角速度，是两个不同参照系中的角速度。这两个不同角速度的变化，在数学上是有一定关系的。
由于太阳系质心参照系是一个惯性系，而太阳和太阳系的行星都是绕太阳系质心运动的，不是绕太阳运动的，因此只有太阳和行星绕太阳系质心运动的轨道角动量总和，才是理论上唯一有资格符合“角动量守恒原理”要求的物理量即：太阳和太阳系行星绕太阳系质心运动的轨道角动量总和是一个常量。
应该指出的是：由于太阳在太阳参照系中的运动速度恒等于零，而太阳相对于太阳系质心来讲具有一定的轨道角动量，因此行星绕太阳运动的轨道角动量总和，在理论上必然不符合“角动量守恒定律”的要求即：行星绕太阳运动的轨道角动量总和不是一个常量。
下面我们通过理论分析再证明一下上面的结论。
当行星在近日点绕质心H运动时。假定行星此时在A0点（A0点此时是近日点），太阳（或M-Mg质心）此时位置在B0点。假定A0B0线段上的H点是太阳系质心。此时线段B0A0＝距离R1。假定线段HA0＝距离RH1。线段HB0＝距离RS1。
当我们用太阳（或M-Mg质心）做极坐标系的原点，用A0点是做极坐标系的起始点时。那么我们利用太阳（或M-Mg质心）极坐标系，可以分析说明行星绕太阳（或M-Mg质心）运动的规律。
当我们用质心H做极坐标系的原点，用A0点做极坐标系的起始点时。那么我们利用质心H极坐标系，可以分析说明行星绕质心H运动的规律。
当行星从A0点开始运动一段时间后。假定行星此时运动到AX点，太阳(“M-Mg质心”)此时运动到BX点。当我们同时在太阳质心（或M-Mg质心）和质心H两者上观察行星运动时，那么行星绕质心H运动的极角ω，与行星绕太阳（或M-Mg质心）运动的极角θ两者的关系可以利用下面的图形来说明。
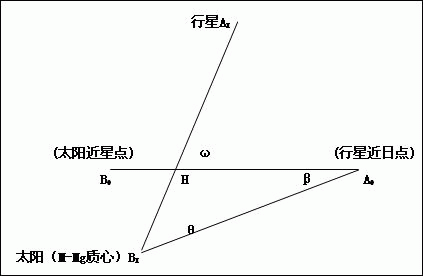
由于太阳（或M-Mg质心）也是绕质心H运动，因此极角ω与极角θ两者一般是不相等的。两者的差角β＝±(ω-θ)。差角β的大小，随着行星和太阳（或M-Mg质心）两者的相对运动而发生周期性的变化。当极角θ在
≤θ≤18的范围内变化时。由于差角β的变化方向与极角θ的变化方向相反，因此差角β此时不大于零即β≤。当极角θ在18≤θ≤36的范围内变化时。由于差角β的变化方向与极角θ的变化方向是相同的，因此差角β此时不小于零即β≥。
当极角ω＝（或者当ω＝18）时，此时差角β＝。当极角ω＝9（或者当ω＝27）时，差角β此时达到最大值β0。本文把β0称为行星的极角系数。我们利用质点运动学可以确定：行星极角系数β0与行星质量MG成正比。与太阳（或M-Mg质心）质量MS成反比。
假定线段BXH＝距离RS。我们利用三角形A0HBX可以得到下面的关系式。
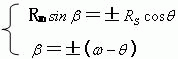（13）
我们利用上面的关系式可以得到下面的关系式。
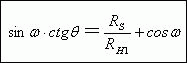（14）
我们利用关系式（1）可以得到关系式。
。由于距离R1（即线段B0A0）是太阳（或M-Mg质心）极坐标系的起始轴线，因此距离R1是一个已知量。我们利用关系式（7）可以得到下面的关系式。
由于极角θ发生变化会使距离R的大小（即线段BXAX的大小）也发生变化，因此距离R是一个变量。把关系式（14）对时间t进行微分后，可以得到下面的关系式。
（15）
当我们利用
同时乘等号左边和等号右边两个关系式后，在利用关系式（9）可以得到下面的关系式。
（16）
由于距离R是行星质心到太阳（或M-Mg质心）的距离。角速度是行星绕太阳（或M-Mg质心）运动的角速度，因此行星绕太阳（或M-Mg质心）运动的角动量LS等于下面的关系式即：
（17）
当上面关系式中的极角θ＝时。由于极角ω＝，sinθ＝sinω＝0，距离R＝距离R1，因此行星绕太阳（或M-Mg质心）运动的径向速度
。由于行星绕太阳（或M-Mg质心）运动的角速度，此时与行星绕质心H运动的角速度，相等（即
），因此行星在近日点绕太阳（或M-Mg质心）运动的角动量
当极角θ＝9时。由于9＜极角ω＜18，＜sinω＜1，sinθ＝1，ctgθ＝0，行星的径向速度
，因此上面关系式中的等号右边的关系式
。于是行星绕太阳（或M-Mg质心）运动的角动量LS此时等于下面的关系式。
上面的分析结果说明：行星绕太阳（或M-Mg质心）运动的角动量LS不是一个常量，而是一个变量。于是我们可以得到结论：开普勒“行星运动面积相等定律”是一个错误的定律。
由于行星和太阳（或M-Mg质心）两者绕质心H运动的角速度是，因此我们利用关系式（12）可以确定：行星和太阳（或M-Mg质心）两者此时具有的动能和引力势能之和E，等于下面的关系式。
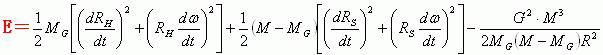
把关系式（7）和关系式（8）两者代入到上面的关系式中，此时我们可以得到下面的关系式。
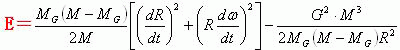
当行星在近日点运动（或者行星在远日点运动）时，此时行星的径向速度。把该关系式和关系式（10）两者代入到上面的关系式中，我们可以得到下面的关系式。
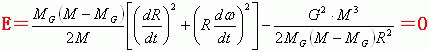（18)
上式的分析推导结果说明：在质心H参照系中，行星和太阳（或M-Mg质心）两者所具有的动能和引力势能之和E始终等于零。或者说：行星和太阳（或M-Mg质心）两者在太阳系质心参照系中，是按照“两者动能之和等于两者间引力势能”的路径绕太阳系质心进行运动的。
第八节、行星绕太阳（或M-Mg质心）运动的周期。
假定行星到太阳（或M-Mg质心）的距离是R。我们根据牛顿力学和关系式（11）可以确定：行星的向心加速度aH等于下面的关系式。
由于行星是绕质心H运动的，因此向心加速度aH应该是指向质心H的，不是指向太阳（或M-Mg质心）的。我们根据上式和关系式（7），可以得到下面的关系式。
上式中的变量RH是行星到质心H的距离。当行星绕质心H运动的时间非常短时，此时由于距离RH变化量dRH非常微小，因此向心加速度aH的变化量daH也同样非常微小。于是我们可以把距离变化量dRH看成是，加速度aH保持不变的运动结果。根据“直线匀加速运动规律”我们可以得到下面的关系式。
由于行星在近日点和远日点两个位置的径向速度
。当行星到质心H的距离RH，从近日点距离RH1变化到远日点距离RH2时。行星绕质心H运动所应该花费时间t等于下面的关系式。
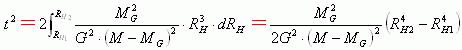
由于行星绕质心H运动的公转周期T＝2t。因此行星绕质心H运动的公转周期T应该等于下面的关系式。
（19）
由上式可知。行星绕质心H运动轨道圆，那么行星绕质心H运动公转周期T小。行星绕质心H运动轨道扁长，那么行星绕质心H运动公转周期T大。
我们利用关系式（7）可以得到下面两个关系式。
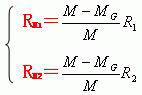
由于行星绕质心H运动的公转周期，与行星绕太阳（或M-Mg质心）运动的公转周期相等，因此把上面的关系式代入到关系式（19）中，我们可以得到行星绕太阳（或M-Mg质心）运动的公转周期T。
或
（20）
由上式可知。行星绕太阳（或M-Mg质心）运动的轨道圆，那么行星绕太阳（或M-Mg质心）运动的公转周期T小。行星绕太阳（或M-Mg质心）运动的轨道扁长，那么行星绕太阳（或M-Mg质心）运动的公转周期T大。
第九节、行星绕太阳系质心运动轨道应该满足的约束条件。
水星近日点每世纪进动5601秒。利用牛顿和开普勒的理论学说只能解释5558秒，还有43秒的进动无法解释。人们虽然可以用“广义相对论”来解答这个问题，但“广义相对论”也只过是仅仅从几何学的角度计算出了这43秒。它并没有从物理学角度向人们说明，水星近日点为什么会发生进动。
“广义相对论”从几何学角度计算出的这43秒，应该看成是太阳影响的结果，而不是其它行星影响的结果。因为是太阳质量使时空弯曲了，而不是其它行星的质量使时空弯曲了。其实水星轨道的进动，根本与“广义相对论”无关，它只不过说明了人们分析解释行星运动规律的理论不完善，或存在着缺陷。
由于太阳是绕太阳系质心运动的，而所有的行星也分别绕太阳系质心做周期不同的运动，因此太阳绕太阳系质心运动的速度，以及太阳到太阳系质心的距离都是不断变化的。受其影响太阳系的每一个行星绕太阳运动的轨道必然会发生一定的变化。利用太阳绕太阳系质心的运动来解释行星轨道的进动问题，比利用太阳质量产生的时空弯曲来解释行星轨道的进动问题，显然要更合理、更科学。
下面我们分析讨论一下，行星绕太阳系质心运动轨道应该满足的约束条件。
由于行星绕太阳（或M-Mg质心）运动轨道上的每一点，到太阳（或M-Mg质心）的距离RX，都小于该轨道点的曲率半径
，因此行星轨道上的每一点，都应该具有椭圆曲线的性质。由于近日点曲率半径
比远日点曲率半径
小，因此近日点的椭圆曲线与远日点的椭圆曲线是两条不同的曲线。于是不同的轨道点就应该具有不同的椭圆曲线。这些不同的椭圆曲线应该具有一个共同的焦点。该焦点就是太阳（或M-Mg质心）。
在太阳（或M-Mg质心）参照系内。由于行星轨道上的近日点曲率半径
，比近日点到太阳（或M-Mg质心）的距离R1大（即
），因此近日点到太阳（或M-Mg质心）的距离R1，是椭圆曲线公式中最小的焦点半径。此外，由于行星轨道上的远日点曲率半径，比远日点到太阳（或M-Mg质心）距离R2大（即
＞R2），因此远日点到太阳（或M-Mg质心）的距离R2，也是椭圆曲线公式中最小的焦点半径。
假定行星绕太阳（或M-Mg质心）运动轨道上，某一点A的椭圆极坐标公式(该公式不是行星运动轨道的极坐标公式)，等于下面的关系式。
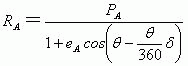
上式中的变量
是行星每绕太阳（或M-Mg质心）运动一周（即36后），行星轨道进动的秒数。当极角
点是近日点时。由于焦点半径PA＝P1＝R1，因此近日点椭圆离心率e1应该等于下面的关系式。
即 
当行星运动到远日点位置时。由于极角
，焦点半径PA＝P2＝R2，因此远日点的椭圆离心率
。于是近日点和远日点两者的椭圆离心率相等即
。如果行星的质量Mg越小，那么行星蛋圆轨道近日点和远日点两者的椭圆离心率e就越小。而近日点和远日点两者的椭圆曲线就越圆。同时，其它轨道点的椭圆曲线也越圆。从这一点来讲，由于椭圆离心率
始终与行星和太阳（或M-Mg质心）两者，到质心H距离的比值相等即
，因此我们可以确定：行星蛋圆轨道每一点的椭圆离心率都是相等的，即。
（21）
假定极角
从近日点的矢径R1（即行星到太阳或到“M-Mg质心”的距离）开始变化。当极角
在9≤ ≤18范围内变化时。由于远日点距离R2是椭圆曲线公式内最小的焦点半径，因此上面的椭圆极坐标公式中的余弦变量cos
在9≤
≤18范围内，就应该比零大,或者等于零（即cos
≥0）。于是行星绕太阳（或M-Mg质心）运动的“蛋圆轨道极坐标公式”，可以假设成下面的公式。
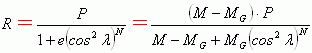（22）
上式中的极角λ=常数
（或者N＝1）。在上面关系式中。极角λ＝的轨道点是近日点，或者是远日点。由于近日点和远日点两者的曲率半径，与椭圆曲线的焦点参数相等，因此近日点的焦点参数
，而远日点的焦点参数
。由于焦点参数P1＜焦点参数P2，因此行星绕太阳（或M-Mg质心）运动的，蛋圆轨道极坐标公式中的焦点参数P不是一个常量。焦点参数P是极角λ的函数即P＝f（λ）。
函数P＝f（λ）具有周期性变化的特性。假设极角λ＝的轨道点是近日点时。根据关系式（22）可以确定：焦点参数P在近日点达到最小值，即近日点的焦点参数
。当行星运动到远日点位置时。由于极角λ＝18时，因此焦点参数P在远日点达到最大值，即远日点的焦点参数
。
行星近日点和远日点到太阳（或M-Mg质心）距离的差为
。由于行星距离的变化与极角λ的变化相关，因此焦点参数P＝f（λ）函数可以假设成下面的函数形式。
（23）
应该指出的是：由于上式函数是根据关系式（21）和关系式（22）两式分析推导出来的，而这两个关系式，仅仅是一种理论上的推测，并非是从天体的实际运动中总结归纳出来的，因此上式函数是否能正确地反映说明行星的实际运动，还需要有关的专家和学者从理论和实际两个方面进行审查验证。
综合以上的分析和讨论，行星绕太阳（或M-Mg质心）运动的蛋圆轨道所应当满足的关系式为：
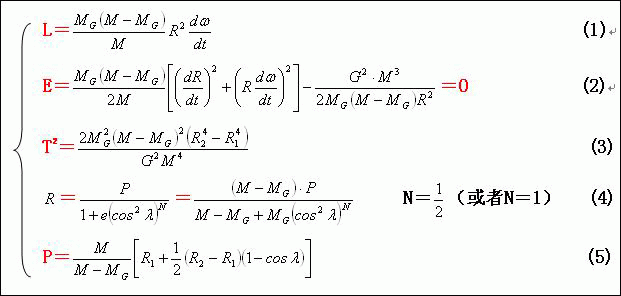（24）
在上式的方程组中:
第(1)式是行星绕太阳系质心运动的“角动量守恒定律”，式中的极角ω是行星绕太阳系质心运动的极角。式中的R是行星到太阳（或M-Mg质心）的距离。
第(2)式是行星和太阳（或M-Mg质心）两者绕太阳系质心运动的“能量守恒定律”。
第(3)式是行星绕太阳（或M-Mg质心）运动的“公转周期定律”。式中的R1是行星近日点到太阳（或M-Mg质心）的距离。而R2是行星远日点，到太阳（或M-Mg质心）的距离。
第(4)式是行星绕太阳（或M-Mg质心）运动的“轨道定律”。式中的R是行星到太阳的距离。
第(5)式是行星绕太阳（或M-Mg质心）运动的蛋圆轨道的“焦点参数定律”。式中的R1和R2分别是行星近日点和远日点，到太阳（或M-Mg质心）的距离。
——完——
——2002年6月4日于济南——
论文作者：王建华
电子邮箱：wangjianhua850@msn.com
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑