物理科学探疑-网友天空-宇宙观念-月球轨道不符合万有引力概念
月球轨道不符合万有引力概念
芦光耀
计算机可准确地计算出月球轨道。
我们知道，按万有引力公式来计算，地球对月球引力的平均值
，太阳对月球引力的平均值
。因此，按万有引力观点，既使是近似计算月球绕地球的平均角速度，太阳对月球的引力也绝不能忽略。计算机计算表明，在只考虑地球对月球引力
的情况下，计算出的月球轨道与实际情况相当符合。在同时考虑地球对月球引力
同时作用于月球时，算出的月球轨道与实际情况的偏差非常之大，以至于月球经若干时间后，将脱离地球的引力范围。这说明太阳和月球之间并不存在引力关系，这正是“R物质”理论的结论（注1）。同时也说明万有引力的概念是错误的。下面说明一下计算机计算月球轨道原理。
间间隔dt（即等步长），以微分形式从地球的初值点逐点向下推算。设t=0时，地球的初值点为r0,v0和
由于dt是人为设定的，是已知的，因此地球到达1点的近似值v,r和a可由上式算出，算出1点值后，可把1点值作为初值，按步长dt继续推算出下一点的值，如此，可推算到第n点。由于dt值取得越小，递推的精度越高，我们可据此来控制计算误差。
设要计算地球在t=T时的r值，要求计算误差为e，t=0时的初值
为已知。我们可将0到T的时间间隔划分为n个dt，即令计算步长dt=T/n,然后根据上述，按步长dt从初值点推算到
时的r值。然后将dt二分，即令计算步长dt1=dt/2,再按此新步长值dt1从初值点算到
时的r值为r2，比较一下二分前后的r值，即看一看是否满足条件
,若满足条件，则r2的值即为所要求的r值，若不满足条件，则继续二分，按新的步长值再从初值点算到t=T时刻，直到新算出的r值满足条件，其中r和r2分别为二分前后的r值。
以上为矢量表达，实际计算中，可将矢量
。于是，它们的初始值分别为
。下面给出地球从初值点经dt时间运行到下一点的递推式，
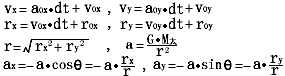
控制误差范围的条件为
分别为二分前后在x,y方向的r值。
以上仅为计算机计算地球轨道的原理。实际上，每二分一次，从0到T时间范围内的dt数量将增加一倍，计算机计算的工作量也将增加一倍。由于计算机的计算速度有限，因此二分次数也是有限的。为提高计算精度，减少计算机的计算工作量，有一些标准化的方法（注2），在此不再熬述。
由上述可知，计算机计算星球轨道主要有两个要点。一是列出递推式，二是确定误差范围的条件。
月球轨道计算见下页。
注释1：“R物质”理论是本人提出的。
注释2：参见“计算机数值计算方法及程序设计”一书。该书由周煦编著。于2004年10月由机械工业出版社出版。
下面分析一下月球轨道的计算。设月球轨道平面和地球轨道平面重合。由于月球绕地球运行，因此应建立动坐标系如图1-3。
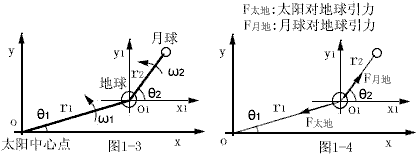
月球在x,y方向的受力为：
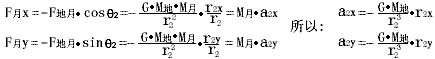
其中
在x,y方向的投影。根据点的加速度合成定理，
月球绝对加速度=月球牵连加速度+月球相对加速度，可得月球绝对加速度a在x,y方向的投影为:
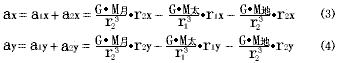
设a的初值为
的初值为
这样，地球和月球从各自的初值点同时出发，经dt时间后，地球就到达了它的下一点
，于是可得如下递推式：
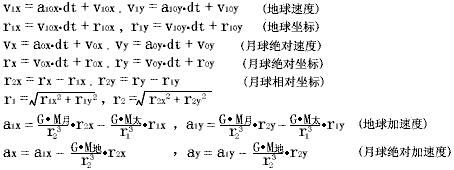
为控制计算误差须同时满足4个条件即：
。
其中
分别为二分前后算出的地球坐标。
在考虑太阳对月球有引力的情况下，月球运动的分析见下页。
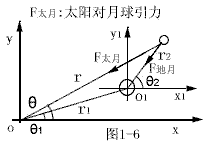
在考虑太阳对月球引力的情况下，月球受力如图1-6。
地球加速度a1在x,y方向的投影仍为前面的(1),(2)式。
太阳对月球的引力为：
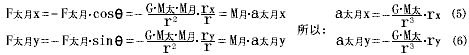 其中
|
 |
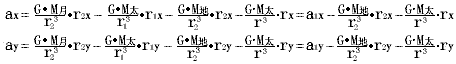
设a的初值为
, r的初值为
。这样，地球和月球从各自的初值点同时出发，经dt时间后，地球就到达了它的下一点
，于是可得如下递推式：
其中
分别为二分前后算出的地球坐标。
再次说明一下，以上月球轨道的计算仅是计算机计算原理，实际编程应采取一些标准化方法，以提高计算精度，减少计算机的计算工作量。
月球轨道的三维坐标计算和上述原理大同小异。不过，按月球和地球的实际运行情况来看，采用二维坐标计算已足够了。
目前，在月球轨道计算上，我已做到了，一天的计算误差e<0.001米（即在x,y轴方向的计算误差e）,也就是说一年的计算误差e<365×0.001=0.365米。
下面分两种情况，让计算机来计算一下月球轨道。
第一种情况：不考虑太阳对月球的引力。下面给定一组初值。
第二种情况：考虑太阳对月球引力。
初值和上面大体相同，下面只给出不同部分。
当取计算时间t=240天时，月球和太阳的距离r=9.23343114643×1011米，该值已大于木星和太阳的距离，说明月球已脱离地球的引力范围。
作者：芦光耀
日期：2006年10月23日星期一
住址：北京市丰台区东高地三角地37栋丁门四楼111号
电话：68751647
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑
为由太阳对月球引力而使月球产生的加速度。