物理科学探疑-网友天空-系统观点-严正岗-宇宙边缘物体的运动行为
宇宙边缘物体的运动行为
严正岗
宇宙有很多的迷团使人困惑不解，本文将思考和回答以下四个问题。第一宇宙星系的膨胀是永久型的还是震荡型的？第二宇宙向外发射的基本粒子是否还能回来？第三从宇宙外看宇宙，宇宙是黑色的吗？第四比光还快的快子在宇宙中的运动也是震荡的吗？对这些疑问的解答，笔者是通过对各个物体（包括基本粒子和光子）在宇宙边缘的运动行为的研究来完成的。
一 各种物体在宇宙边缘的运动规律
动量定理是所有运动物体必须遵循的运动规律，这是本文的一个先决条件。另外一个条件是宇宙的旋转产生了明显的类磁效应[1]。前者告诉我们，当考虑了相对论后，以速度
运动的物体m当受到合力
后，能满足的公式为
而后者说明物体所受的合力，应以以下式子来表示
（1）
表示旋转方向的单位矢，而
，M、R0和ω分别为宇宙的质量、半径和旋转角速度。对相对论质量公式
求导，有
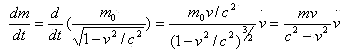（2）
式（1）和式（2）代入动量定理，注意消去m和dt有
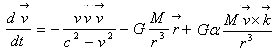（3）
用极坐标来表示上式，并注意到
各有一个分量，有
（4）
（5）
上两式中
式（4）、式（5）就是各种物体在宇宙边缘的运动规律，
它的解极为困难，为了说明问题，我们来讨论以下几个简单情形。
二 物体在不旋转的宇宙中作径向运动
如果物体在不旋转的宇宙中，只作径向的运动而没有横向的运动，即令ω=0、θ=0,
那么必有
，因此式（4）可为
两边乘以dr，并注意到v=dr/dt，上式积分后可得
（6）
A、 A'
均为积分常数。若初始条件为，r=R0，v=v0，则
讨论：
1 、当v0<c时，r增大v减少，若M是宇宙质量且足够大[]时，则r很小时，v可为0。即宇宙是震荡型的。
2 、当v0>c时，将A代入式（6），整理后可得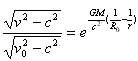
，显然r增大，v也增大，既快子能跑到无穷远，一去而不复返。
3 、当v0=c时，即光子的运动。将式（6）改写为
，因为m=hf，f为光子的频率，所以式（6）可为
（7）
r增大时，f减少，这也就是引力红移。但是f不可能为零，所以从宇宙外看宇宙，宇宙不是黑色的。
以上分析说明，宇宙是震荡型的但不封闭，宇宙能量在不断地疏散和消失，这样的宇宙模型人们不能接受。
三 物体在不旋转的宇宙中作一般运动
物体在不旋转的宇宙中的一般运动，就是指θ≠0。讨论如下：
1 、对于v0<c的物体，由于在径向的分量减少了，所以物体一定会返回。因此宇宙一定是震荡型的。
2 、对于v0>c的物体，若快子[2]的运动
由式（2）和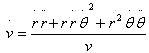
，所以dm/（mdt）≈0，式（4）、式（5）的后一项都没了，其解的形式为
（8）
s和e均是常数，式（8）是熟悉的极坐标二次型方程。由于式（5）的解为
若r能达到无穷远（式（6）的讨论提示），则
这说明式（8）所表示的方程具有渐进线，它是一条双曲线。
3 、对于v0=c的光运动，光子的动量为
为光速矢量，其定义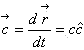为
，因为
标的单位矢和光运动方向的单位矢（这也可用相对论速度公式得到）。由动量定理
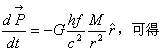
上式在θ方向和r方向式分别为
（10）
（11）
式（10）的积分[3]为
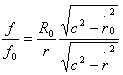（12）
为书写方便，按惯例字母头上带点表示对时间的求导。上式已将初始条件代入，
初始时刻光子的位置、频率和光速在径向的分量。式（11）和式（12）消去f，可得到任意时刻光子的位置和光速在径向的分量的关系[4]，其为
（13）
式中
将上式代入式（12）就得到式（7）。这说明光子的频率变化，不取决初始的方向，只有距离r所决定。式（13）告诉我们，存在着光子径向速度为零的解，这只要满足下式即可
（14）
这说明光子是可以返回的。但若θ很小时，上式是无解的。我们说，总有一些光是接近径向运动的，这样看来不旋转的宇宙不可能是纯黑色的了。但是宇宙是旋转的，只要旋转的角速度足够大，就能保证对于每条光线来说都不是小角度的。因此我们认为宇宙可能是绝对黑色的了。
四 物体在旋转的宇宙中的运动
1 、宇宙赤道边缘星系的运动
在大尺度的情况下，宇宙赤道边缘星系的运动，是和宇宙旋转运动同步的。因此它的角速度就是宇宙的旋转的角速度，它和宇宙中心的距离，就是宇宙的即时半径。这样的理解和均匀膨胀的宇宙模型是一致的。通过对这样的模型的研究，我们能得到宇宙赤道边缘星系的运动的螺旋性轨道方程。
（15）
（16）
从式（15）我们看到，右边有一个正项，它表示了宇宙有一个斥力因素，正是这个斥力因素才是宇宙膨胀的动力原因。由于方程的时间连续性，因此宇宙并非有一个突发的爆炸。我们认为宇宙是初始是缓慢膨胀的，它的横向速度接近光速，而径向速度为零。于是我们将宇宙的初始条件写为：
为分别为宇宙膨胀的初始半径和速度。我们将宇宙的初始条件代入上两式，就可以得到宇宙膨胀的条件和宇宙的初始半径的下限。注意到
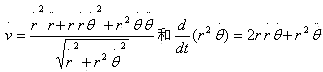
我们可将式（16）写为
。由式（15）宇宙初始膨胀的条件为
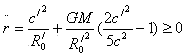（17）
因为
这个值为目前宇宙半径的一半左右。
从式（15）和式（16）直接解轨道方程很困难，我们用螺旋性轨道方程，用待定系数法间接取得，只要满足初始条件就可以了。我们试用的螺旋性轨道方程为
（18）
当θ=0时
（19）
因为
（20）
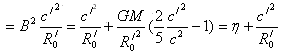
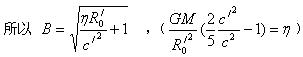
因此有
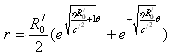
这就是宇宙赤道边缘星系的螺旋性轨道方程（很象银河系外部旋臂的运动）。这方程能否说明宇宙是震荡型的吗？粗看起来当θ无穷大时，r也是无穷大的。但θ不可能无穷大，因为式（5）告诉我们，在宇宙中宇宙角动量不是守恒的，所以宇宙的角速度可以为零。而从式（20）知道，当宇宙的角速度为零时，它的径向速度也为零。宇宙从此开始逆转运动。
2 、宇宙赤道边缘快子的运动
由质子和电子的结构[]我们了解到快子的速度是极快的，一般认为是远大于光速的。这样的粒子粗看起来是跑得很远，好象是不能回来的，至少在静止的宇宙中是如此的。但是在有旋转运动的宇宙中，这情形正好相反。由于宇宙对快子有较大的类磁作用，使得快子就有了返回的可能。下面我们来详细地进行讨论。
对时间的变化有式（2）可写成
。因为质量的变化几乎为零，而动量的大小也是几乎不变化的，所以速度的大小变化也很小，因此可认为
所以式（4）和式（5）可写成
（21）
（22）
式（22）的一次积分为
（23）
A为积分常数。将式（23）代入式（21）并一次积分[5]为 可得
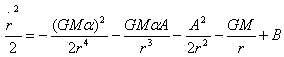（24）
B为积分常数。将初始条件代入上两式，可得[6]
（25）
β为初速和径向的夹角。因为B>0且很大，所以总有一个位置r，使得快子的径向速度为零。这意味着快子的运动有周期性的，它的轨迹可能是封闭的。有一个有趣的现象，将式（25）和式（23）、式（24）代入速度平方的公式可得
这和经典力学的实体物体结论一样。
快子的轨迹复杂可从式（23）来讨论角速度来看出。将上式代入已经代入常数的式（23）可得
（26）
若
说明快子始终是逆时针运动的，它的轨迹可能相对简单；若
先大于零且减小，变为零后为负值，它的轨迹就较为复杂了。
3 、宇宙赤道边缘光子的运动
由光子的动量定义
和对其时间求导而得到的动量定理为
（27）
用极坐标来表示上式，并注意到
各有一个分量，有
（28）
（29）
以上方程本人无法得解，望看客们谅解。但光子一定是可以返回的，也就是说宇宙一定是绝对黑色的了。
参考文献与附录
[1]见《宇宙空间并非弯曲》
[2] 见《质电统一理》
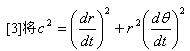（a）
求导（按惯例字母头上带点表示对时间的求导）有
（b）
式（a）代入式（b）消去θ的一次导数后，代入式（10）消去θ的二次导数并用分离变量法可得
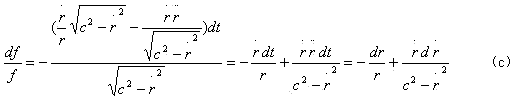
积分上式可得
，将初始常数代入，可得到积分常数C的值，整理后可得到式（12）。
[ 4 ]将式（a）代入式（10）消去θ的一次导数后，式（10）用分离变量法可得
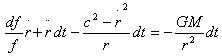将式（c）代入上式，再两边乘以dr/dt，注意到
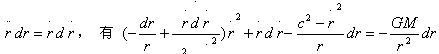， 化简后可得
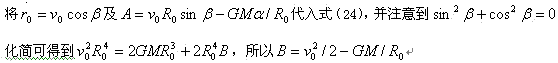
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑