物理科学探疑-网友天空-系统观点-严正刚-银河系的运动速度(修正)
银河系的运动速度
上海市宝山中学 严正岗
[内容提要]：本文为原创性论文。本文将万有引力定律和狭义相对论结合，得到了物体间相互作用的另一种表达式。在光运动情况下，该表达式显示了明显的狭义相对论效应。本文认为正是这一效应使得光线通过太阳附近时产生了更大的偏转。而光线通过太阳附近时的偏转角是随所考察的光子的运动方向和银河系运动方向的夹角改变而改变的。
若在银河系中的黄道平面外能测得偏转角的数据且是改变的话，则证明了广义相对论是错误的。同时可以计算出银河系相对于宇宙中心的绝对速度（其下限为0.707c）。然后利用哈伯定律，很容易得到银河系到宇宙中心的距离，因而可建立宇宙空间坐标系。
关键词：万有引力定律的狭义相对论效应 ; 绝对速度；宇宙空间坐标系
银河系和其它星系一样，由于宇宙的膨胀而在高速地运动着。在地球上已观察到其他星系的高速退行，证明了银河系也应该有能和真空中光速相比拟的运动速度。在银河系之中的我们，虽然能用多谱勒效应测定其他星系相对于银河系的退行速度，但我们无法仅用该方法来测定包括银河系再内的所有星系相对宇宙中心的退行速度，所以我们必须寻求其它方法，这就是利用万有引力定律的狭义相对论效应。有一个百年经典实验将有助于我们的研究，那就是光线在引力场中的偏转。在这里我们不认为光线的弯曲是空间的弯曲引起的，而以为是光运动的狭义相对论效应所反映的。我们的理论认为，由于光具有多谱勒效应的红移和蓝移现象以及光具有最大速度的这两个特殊性，使得物体对光子的作用不仅有万有引力，还有和光运动方向有关的并和观察点速度联系的附加引力，在日全食中我们将能观察到这附加的引力产生的效应——正是因为这附加的引力使通过太阳附近的光线发生更大的偏转。通过对偏转角度的研究，我们可得到银河系相对宇宙中心的退行速度的下限，再用多谱勒效应和相对论速度相加原理，我们就可以得到其他星系相对宇宙中心的退行速度。另外，如果我们知道银河系的速度的话，根据哈伯定律，我们就可得到宇宙中心的位置（绝对原位）到银河系的距离，从而建立绝对的宇宙空间坐标系。
一、万有引力定律的狭义相对论效应
在高速运动情况下，物体间所遵循的万有引力定律在特殊情况时会产生狭义相对论效应。不过如果用在惯性系里测量的物理量（如质量和速度），而在该惯性系里表示物体间的万有引力定律，那是不会产生狭义相对论效应的。这是因为在下文中我们将说明，万有引力定律在任何惯性系里表达式是完全一致的原因（这里我们有一个假设，万有引力定律在另一个非银河系的惯性系里成立）。但是当我们将某一惯性系测量的物理量在另一惯性系里来表示物体间的万有引力定律时，则会出现引力定律公式的变形。这个变形公式对于光子这一特殊物质，或对于有更多自由度的体系，便会产生明显的狭义相对论效应。说明如下：
| 为了以后研究宇宙的方便，我们的研究拓宽到宇宙星系间。我们 来研究并希望能得到万有引力定律在宇宙星系间更一般的表达式。为 此我们将实验室搬到宇宙外，并设从宇宙外看宇宙内甲乙两星系的质 量和速度分别为m、v和m,、v,，它们的距离为r，而u为另一惯性系 的速度，v、v,、u均为相对宇宙中心的绝对速度，它们的位置和速度 方向如图1所示。用狭义相对论和万有引力定律，我们可以导出[1] 在 宇宙外来看，甲乙两星系相互作用力的另一种表达式，其为
|
|
而v.u为v、u矢量的点积。不难看出，式（1）其实就是普通的万有引力定律，这只要令u=0即可。它的意义在于复杂的式子里包含了相互作用物体的运动信息。如果运动是特殊的物体（如光运动）或非匀速的物体，那式（1）不可能回到原有的万有引力定律式，这说明在相互作用物体的引力里，也有狭义相对论效应。另外展开式（1）可以看出，它实际上是一个多项式，这和万有引力定律是单项式已经有所区别了，我们认为，如果满足一定的条件，相互作用物体的引力会产生较大的变化。
我们还可以从式(1)看出，万有引力定律在不同的星系里（惯性系）的表达式其实是一致的。我们来看在甲星系里的万有引力定律形式，即将观察仪器放到甲星系里观察。令u=v。因为v.u= u2，所以从宇宙外来看，甲乙两星系相互作用力
将其回到甲星系里，注意到M甲=m/γ，M甲，=m′γ(1-v，.u/c2)， F，=Fγ，因此F，=GM甲M甲，/ ru2，万有引力定律在甲星系里是成立的。特别地，当把甲星系看成是银河系时，万有引力定律成立我们是确信无疑的。因为甲乙星系是任意的，所以我们认为无论从哪个星系来看，万有引力定律都成立，其表达式在任何惯性系里是完全一致的。因此，万有引力定律应该是宇宙中普遍成立的定律。
下面我们讨论式（2）对于最大速度的光运动赋予的特殊性。为了考虑到下文的实用性，我们考察光子在银河系受到的作用力。设甲星系为银河系，乙星系为运动的光子。考察式（2），因为v，=c，所以v，.u/c2=uc/c，uc为u在光运动方向的分量，注意到M甲=m/γ，并将其回到银河系，因此有
m′是实验室光子的动质量，如果用银河系所观察的该光子的动质量m光来表示上式，并考虑我们所考察的光子是运动方向和银河系运动方向的夹角大于900的情形，则我们可以用- uc替代uc，因此上式可表示为[2]
(4)
由于
，即在银河系观察到的光子将受到更大的引力。这就是所谓的万有引力定律的狭义相对论效应。
| 二、 光线弯曲的狭义相对论解释及银河系的绝对速度
1970年3月7日日食时，用近红外光拍摄到了日冕照片，
|
 |
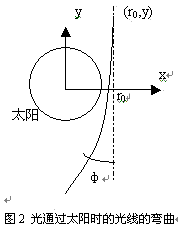u为银河系的绝对速度（太阳相对银河系的速度和银河系本身的速度相比太小，可忽略不计），uc为银河系在光方向的分速度，r为光子到太阳的距离。因为实际测量出光线偏转角很小，所以可以用冲量近似方法计算，如图2所示。求得的光线的偏转角度其结果[3]为
，其中
（5）
的计算结果是0.87，实际值为1.75，所以系数k=2。因为0≤∣uc∣≤∣u∣，所以可解出c>∣u∣≥0.707c，这说明当银河系以大于0.707倍光速的速度和星光有一定的夹角运动时，太阳对光线的作用力就使得光线在通过太阳时发生了1.75”的偏转。
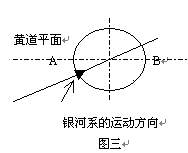
有几个问题需要说明：一是用不同星光做实验，被测光线的偏转角会不会有不同的结果的。我们认为这是不会的，因为虽然不同的星光质量是不一样的，但计算时式中m光可以消去，我们无须知道它的大小，而多谱勒效应留下的银河系的速度关系在式（4）中是一样的；二是由于在地球上测量是被限制在黄道平面内的（如图三），在不同的时间里测量，使得被测光线和银河系的运动方向不一致，会不会影响测量的结果。我们认为也不会，因为式（3）中银河系在星光方向的分速是平方关系的，无论你在黄道平面内的A点
| 去观测从B处来的星光，还是在黄道平面内的B点去观测从A处来的星光，银河系速度在星光方向的分速的平方是不改变的。这意味着在黄道平面内的任何地方去测量，其结果一定是一样的。事实上从1970年到现在，利用甚长基线干涉技术，十几次观测了太阳对射电源的偏折，基本没有发现测量结果有较大的偏差。另外广义相对论把这一现象看成是空间弯曲的直接结果，但是我们并不这样认为。因为如果光线的弯曲仅 仅是空间的弯曲引起的，那么星光镜象的爱因斯坦环应该是圆形的，即从不同的方向如在黄道平面外去测量，其偏转角度也应该是相同的。而式（5）告诉我们，如果测量点不在黄道平面内，则银河系在星光方向的分速度就会改变，其测量结果一定是会变的。这是判定本理论正确还是广义相对论正确的一个简便的方法。 |
 |
三、宇宙空间坐标系
以上的分析说明，一旦我们得到了光线偏转的实验结果是随银河系在星光方向的分速度改变而改变的，那我们就否定了空间是弯曲的结论。同时我们通过式（5）就可以计算出银河系相对于宇宙中心的绝对速度和银河系在星光方向的分速，从而由cosβ=uc/u，我们就容易地得到星光（或黄道平面）和银河系运动速度的夹角。利用这一夹角和哈伯定律，我们就能确定银河系与宇宙中心的距离，因而可建立宇宙空间坐标系。而其它星系的位置和速度，可根据其相对于银河系的距离和方位来决定。下面作详细说明。
若星光的偏转角是改变的，则式（5）应该成立，即uc和k有确定的函数关系。我们可以在黄道平面外不同的方向（在月球上也可以）多次测量星光的偏转角，并作出式（5）的微分式
（6）
式（6）和式（5）联立，可得到θ和u。在式（5）中，若k取2，则θ为黄道平面和银河系运动方向的夹角。宇宙的原点和银河系的距离则由哈伯定律来决定，其距离为 r=u/H，H为哈伯常数。其它星系的空间坐标可由相对银河系的距离及方位来决定；或用从地球上由多谱勒效应测得其它星系相对于银河系的速度v相对及银河系的绝对速度的值，用相对论速度关系[4]
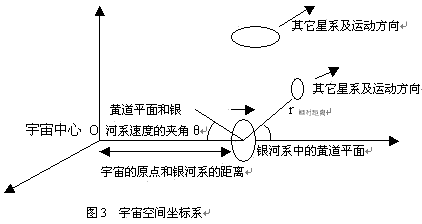
求得其它星系的绝对速度，再由哈伯定律计算出其和宇宙原点的距离，如图4。
附录及参考书目：
1设从宇宙外看宇宙内(实验室)，甲乙两星系的质量和速度分别为m、v和m'、v',它们的距离为r，u为观察仪器所在地的另一惯性系的速度，v、v’、u均为相对宇宙中心的绝对速度，它们的位置和速度方向如图1所示。在乙物体的静系中，乙物体的质量为
我们知道，在相对论力学里，要将力的关系从一个系到另一个系的变换时，只要除以一个因子γ就可以了。所以，如果我们将观察仪器放在宇宙外，观察到的甲乙两星系相互作用力（即在u系里的关系式（２）变换到实验室系里）的关系式就为
作者： 严正岗 上海市宝山中学
家庭地址：上海市宝山区临江二村31号602室
电话：021-56698910（家） 021-56692144*407（单位） 邮编：201900
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑
