物理科学探疑-网友天空-系统观点-严正刚-膨胀的宇宙及其质量公式
![]()
膨胀的宇宙及其质量公式
上海市宝山中学 严正刚
宇宙质量公式
宇宙质量公式是和宇宙模型相联系的,建立不同的宇宙模型,宇宙的总的质量公式也就不同。目前,最热门的大爆炸宇宙模型是符合现代宇宙测量结果的、为大多数科学家们所接收的、比较合理的模型。本文通过对这样的模型研究,运用狭义相对论速度公式和哈勃定律,推导出了宇宙质量公式。然后,通过对各种情况的研究讨论,得到了相应的有意义的结论。
一.膨胀的宇宙
上世纪上、中叶,天文测量得到了极大的发展。胡克反射望远镜首先揭示了远外星系的退行。随后,射电望远镜进一步确认了宇宙背景辐射的存在。这就为膨胀的宇宙提供了最为有力的证据。特别是哈勃定律的发现及宇宙背景辐射的均匀性,为均匀分布的宇宙模型提供了可靠的实验支持。所以,均匀分布的宇宙模型可能是最适合我们的宇宙的。那么均匀分布的宇宙模型和哈勃定律有什么关系呢?
| 我个人认为,如果把宇宙看成是既旋转[1]而又均匀膨胀的话(设宇宙各处密度相等),那哈勃定律实质上是宇宙膨胀的几何特征的必然。说明如下:设有两个星系A和B相距为rAB(见右图),它们对于宇宙中心( 假设存在)的距离矢量为rA和rB,则rAB=rA-rB。如果宇宙是均匀膨胀的,则在时间t内星系A和B(相对宇宙中心来讲)只有径向的变化且规律一样,即可认为后一时刻的距离失量为rA'=krA,rB'=krB因此必有rAB'=krAB。这告诉我们在星系B去观察星系A,星系A必然是背离星系B的,显然我们还可以看到,两星系距离的变化量和其距离成正比 | 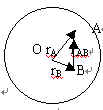 |
rAB=rAB
’-rAB=(k-1)rAB除以时间t并取极限,有
v=lim t→0rAB/t=limt→0(k-1)/t rAB
这告诉我们,两星系的相对速度和相对距离成正比,这便是哈勃定律。其中limt→0(k-1)/t便为哈勃常数。需要说明的是,宇宙的均匀膨胀不是对时间而言的,而是对空间而言的。做一个比喻,如果把宇宙看成是一张地图,当宇宙上各点的位置变化时,就相当于宇宙地图按同样比例地被放大(或缩小),它们各点的位置虽变大(或变小),但相对方位没变。这就意味着如果哈勃定律是这种宇宙模型的几何必然,那么哈勃常数仅仅是这一时刻的几何特征系数,即它表示的是这一时刻的宇宙膨胀率(或者为收缩率,假如宇宙能收缩),因此哈勃常数对时间是可变的。
从这里我们看到,如果哈勃定律是正确的话,那么均匀分布的宇宙模型就有一定的可靠性。诚然,从小尺寸范围看宇宙,由于各星系的离散及它们的密度也可能不一样,所以宇宙并非是完全均匀的。但从大尺寸范围去考察,将宇宙看成是密度均匀分布的也是合理的,这和由分子组成的物体一样,从原子核角度来看,核与核之间是非常远离的,但从宏观角度来看物质则是紧密分布的。
二、宇宙的总的质量
|
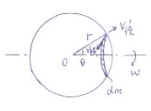
设宇宙的旋转轴为水平轴,如右图所示。现考察位于宇宙中心距离为r的微元星系dm。由于宇宙在旋转,故该星系有横向速度v横=ωrsinθ,ω为旋转角速度。又由于宇宙在膨胀,所以该星系还有宇宙的径向速度v/径,根据哈勃定律 v/径=Hr |
 |
v
径=![]()
这样dm和其静质量dm0的关系可写
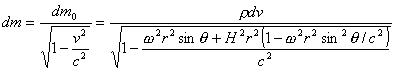 (1)
(1)
上式ρ为宇宙的静密度。将上式积分并做适当简化,可得
![]() (2)
(2)
先在以轴为对称的阴影环带上积分,考虑到dm的对称,dv=2πr2sinθdθdr,因此
![]()
![]() (3)
(3)
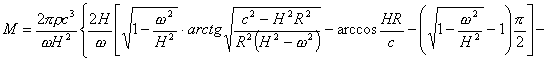
![]()
(4)
这就是宇宙的总的质量公式。从上式可以看到,宇宙的总的质量M是随着H和R的改变而改变的,因此M一定是时间t的函数。就目前而言,宇宙边缘的速度已非常接近真空中的光速,因此有c=HR,所以上式可化为![]() (5)
(5)
这就是目前的宇宙的总的质量公式。
三、宇宙总质量的可能情况的讨论 我们的宇宙及其演变有各种可能情况,如有旋转宇宙和不旋转宇宙;宇宙的爆炸是突发的还是渐进的;未来的宇宙是开放的还是震荡的。这些可能情况是否正确可以用式(4)来探讨。另外,从能量的转化和守恒定律来讲,当宇宙的半径增大时,则宇宙的势能就增大,因而宇宙的质量一定要减小。这是判定宇宙模型是否正确的一个方法。下面我们根据这个原则来进行讨论。 1.不旋转的宇宙 (ω=0) 将式(4)求ω→0的极限[4],其值为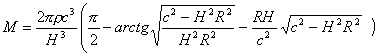
因为大爆炸前H=0,所以大爆炸前的宇宙静质量为
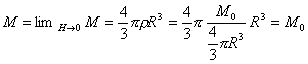
(1) 若大爆炸后,宇宙中各星系的速度并不改变,且认为宇宙边缘速度始终为c。因为c=HR,所以
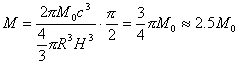
(2).若宇宙的爆炸是缓慢的,即从v0=0开始。因为宇宙蛋半径R0不为0,所以H=0。因此宇宙在爆炸前后的总质量没有发生突变。但就目前而言,因为HR=c,所以
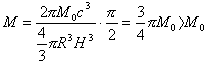
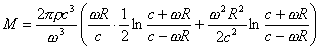 (6)
(6)
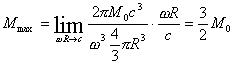
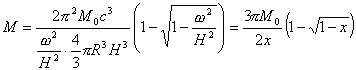
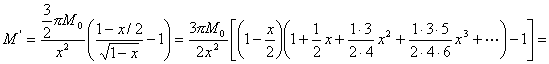
![]()
即M是关于x的单调函数。令x→0,
3.未来的宇宙
目前,未来的宇宙有两种情景,我们对它的可能性进行讨论。
(1).震荡的宇宙:当R最大时,v=0,H=0,ω≠0。令x=ωR/c,代入式(6)可得![]()
![]()
这是可能的。
(2)开放的宇宙:当R→∞时,0<HR≤c,ωR→0,H→0。将式(4)写成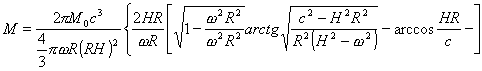
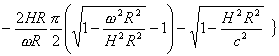
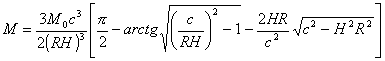
[附录]
[附录]:[2].
令ωrcosθ/c=x,将其微分ωrsinθ.dθ/c=dx,代入原式,有![]()
![]()
![]()
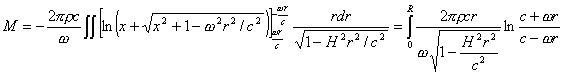
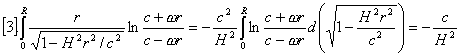
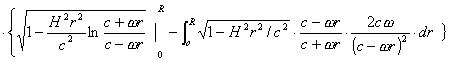
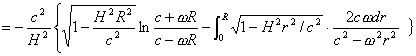 (A)
(A)
令
Hr/c=cosβ,将其微分,Hdr/c= -sinβdβ,所以上式中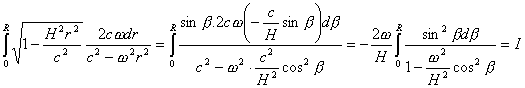
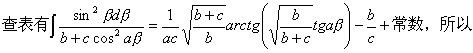
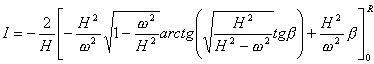
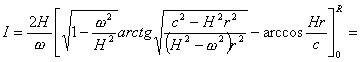

代入式(
A)后,可得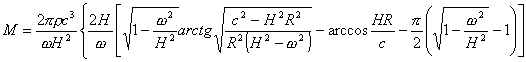
![]()
[4].
注意到![]()
所以式(
4)中,当ω→0时,式中[ ]→0,因而{ }→0,所以可用罗必塔法则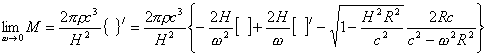
上式中的第一项,再用罗必塔法则,可得
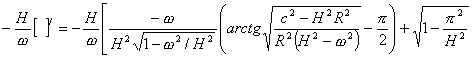
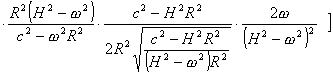
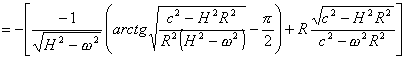
和第二项相加,再减去第三项并取极限,有
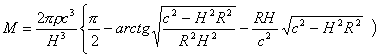
[5].
由式(3),令H=0,则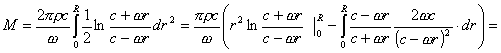
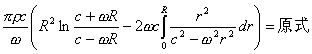
我的通讯方法:
地址:上海市宝山区临江二村31号601室。邮编:201900。电话:021—56698910
工作单位:上海市宝山中学
。 邮编:201900。电话:021—56692144[注:纠正附录3和附录4的交叉错误,纠正时间2001.4.18]
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任
版权说明 © Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任
版权说明 © Copyright Authors
物理科学探疑