物理科学探疑-网友天空-系统观点-肖军-附图
洛仑兹变换式物理解释有误
肖军
【摘要】本文着重论证了洛仑兹变换式不是两惯性系间的坐标变换式，而是电磁波周相不变变换式的一个特例，同时得到与时钟延缓效应和迈克尔逊干涉实验零结果相容的光速与光源运动速度之间存在的关系式。
关键词 电磁波 动光源 变换式 光速
通常人们把洛仑兹变换式看做是两惯性系间的坐标变换式，并把伽俐略变换式看做是其在低速情形时的特例.其实，这是一种错误的认识,在低速情形时，两种变换式的形式虽然相同，但它们的物理含义是截然不同的，伽利略变换式是两惯性系间的坐标变换式，而洛仑兹变换式则是电磁波周相不变变换式。无论在低速情形，还是在高速情形，两种变换式都应成立。为弄清洛仑兹变换式与伽利略变换式的区别，我们不妨先来讨论伽利略变换式的导出过程。
设有两结构完全相同的光源，其中一个光源相对
恒处于静止状态，另一个光源是以速度
时刻两光源位置重合，并且两光源在重合瞬间开始沿
时刻波前到静光源的距离若为
(1)
这就是经典理论中两惯性系间的伽利略坐标变换式，它广泛适用于牛顿力学理论。
人们早已注意到，(1)式不适用于电动力学理论，因为它不能满足波动方程的协变性要求，波动方程的协变性是要求
含有相同波数，满足这一要求的变换式应当这样导出，若用
运动两种情形均沿
分别表示相应光波的固有圆频率。则易写出
间有关系式
(2)
同理，也可写出运动光源沿
(3)
根据
由(2)、(3)两式易导出
(4)
将(4)式代人(2)式，再在(2)式两边同乘以波数
，并令
就可得到洛仑兹变换式
(5)
显然，洛仑兹变换式中的
因而它是电磁波周相不变变换式。洛仑兹变换式与伽利略变换式的区别是它们关于
的定义有所不同，见图l所示。
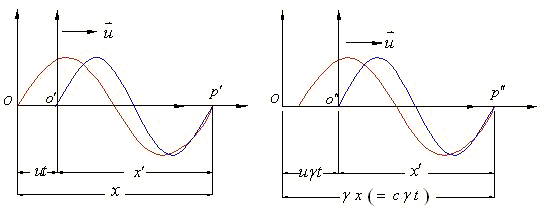
图1
在伽利略变换式中
的定义是
而在洛仑兹变换式中的定义是
点一段距离，也就是
。可是，洛仑兹和爱因斯坦以及当代一些学者都把
点来讨论，进而导致把洛仑兹变换式误视为两惯性系间的坐标变换式。
爱因斯坦还把三维空间说成是四维空间。事实上，三维以上空间仅是一种数学结果，客观上并不存在四维空间。如果存在四维空间，这四维空间的坐标分量应是相互独立，不能相关。可是，爱因斯坦四维时空理论中的时间就不满足这一条件，它是三维空间坐标的函数，即有
也就是说，时间和三维空间坐标是一对因果关系。爱因斯坦把因果混在一起建立起来的四维时空理论是在人类科学史上上演的一场闹剧。
在狭义相对论中，曾把洛仑兹变换式写成形式为
 |
（6） |
并认为式中的
是动静两三维空间坐标中的一维坐标分量。事实上，电磁波波动方程对(6)式变换具有协变性应理解为波动方程的形式与光源运动状态无关，据此(6)式中的不能是动静两系中的坐标分量，而应是光源分别在动静两种情形辐射光波的三维波矢
上的投影长度，即有
它们在静系
中的三维坐标分量为
三维直角坐标轴的正向单位矢量；
若在(6)式两边同乘以
易得到洛仑兹变换式的三维形式必须具有形式为：
 |
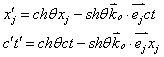（7） |
对于式中系数
在以往的讨论中是通过假设
（8）
而得到
这一结果仅能在波前传播方向
同向情形时成立。
对于波前传播方向不同向情形，(8)式应更正为
（9）
方向上在空间中的传播速度。实验已证实，在
不同向情形，如果令
（10）
(9)式则可写成形式为
（11）
于是，有
（12）
也即有
（13）
都是待定系数。
利用(13)式易导出
（14）
把(14)式代人(13)式，又可导出
（15）
于是，由(10)式和(12)式知
（16）
及
 |
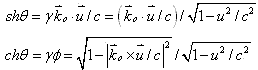（17） |
将(17)式代入(7)式，就可得到肖军三维电磁波相位不变变换式
 |
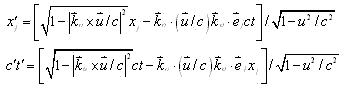（18） |
不难看出，在狭义相对论中所讨论的洛仑兹变换式仅是(18)式在
情形时的结果，此时确有
由于此结果与迈克尔逊干涉实验零结果相容，因此,迈克尔逊干涉实验零结果应看做是支持(16)式和(18)式成立的实验证据。
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑