物理科学探疑-网友天空-系统观点-肖军-论电磁波相位不变变换式的组合变换

论电磁波相位不变变换式的组合变换

肖 军

【摘要】本文着重论述了观测者和场源均运动情形时的电磁波相位不变交换式的组合交换，并由其讨论了电磁场的变换关系式、动体间的电磁作用力以及光速空间方向效应。文中首次提出的场源等效运动速度计算公式和等效变换原理是研究动体电磁现象的理论基础。

关键词 电磁场 相位 变换式 组合变换 作用力

    在建立动体电磁理论时，无需引入狭义光速不变假设和狭义相对性原理，更无需放弃绝对运动概念。在经典绝对时空框架内，只要以肖军三维电磁波相位不变变换式为数学基础，就可建立起完备自洽的动体电磁新理论。本文所要讨论的两个电磁波相位不变变换式的组合变换是该理论的重要组成部分。

1    组合变换

    在文1中笔者推导具有群性的电磁波相位不变变换式

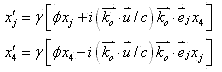(1)

时，作了相对静系S场源以速度 运动、观测者静止假设，式中

是波前在真空中最大传播速度。由于(1)式仅适用于时。电磁波固有圆频率运动场源不能辐射周期变化电磁波；在时，运动场源虽然能够辐射电磁波，但因是虚量，电磁波的振幅将按指数迅速衰减为零。

    通常把电磁波的固有圆频率看做是运动场源内电子跃迁固有圆频率其实这是两个不同概念，在非真空情形有

    现在我们讨论相对静系S观测者运动情形。若把(1)式中的就可得到适用于观测者以速度运动、场源静止情形时电磁波相位不变变换式是

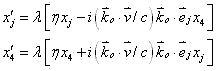(2)

式中

    我们应注意到，(1)、(2)两变换式都能使波动方程协变，而且比洛仑兹变换式具有更强的群性。如果两个洛仑兹变换式的组合变换是群的一个变换，必要求两个变换式中的速度是在同一方向上。而对于(1)、(2)两式则不同，只要两式中的是否在同一方向上，其组合变换都是群的一个变换，并可写成形式为

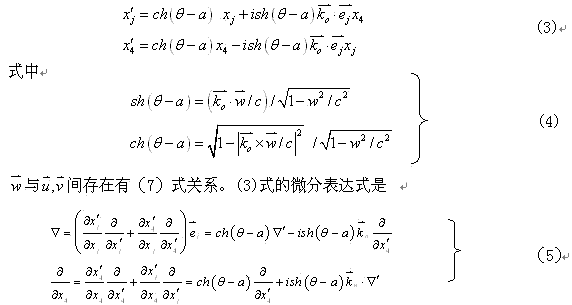
2、源等效运动速度

    依据(3)式与(1)式形式相同，笔者认为，(3)式就是(1)式中的场源相对静系以速度运动情形时的电磁波相位不变变换式。因而，在电磁观测效应方面，对于前述场源以速度运动情形，可按观测者静止、场源以速度是一种等效变换，其中为场源的等效运动速度。

    场源的等效运动速度间的关系式可以这样导出，组合(1)、(2)两式变换，并与(3)式比较易知

即有

                                   (6)

将(6)式两边自乘后，就可得到

                           (7)

(7)式可简化为

这是我们非常熟悉的爱因斯坦速度合成公式。

    均都远小于光速但这只能是在量值上近似相等罢了，在概念上则是两回因此，对于相对静止的运动场源和观测者，其间观测到的电磁效应同观测者和场源相对静系均静止情形时观测到的电磁效应等价。正因为这样，我们在确定静止场源辐射的电磁场强度时，并非要求场源和观测者相对静系处于静止状态，而是要求观测者和场源间要处于相对静止。

3.    电磁场的变换关系

    相对静系S而言，静止电场源激发的电场和静止磁场源激发的磁场在自由空间中满足麦克斯韦场方程组

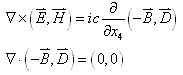(8)

这里所说的电场源是指观测者相对场源静止时仅测有电场存在的场源，如点电荷就是一种电场源；而磁场源是指观测者相对场源静止时仅测有磁场存在的场源，如磁体、载流导线等都是磁场源。无论是电场源，还是磁场源，当它们相对观测者运动时，观测者将同时测有电场若假设电场也满足麦克斯韦场方程组，即满足

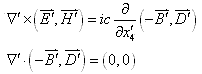(9)

利用变换式（5）可导出

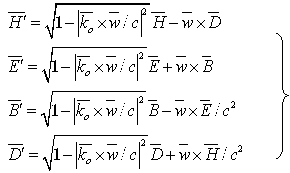(10)

都应是观测者相对场源静止时测得场源激发的电磁场强度，否则，就不可能得出正确结果。利用（10）式可证

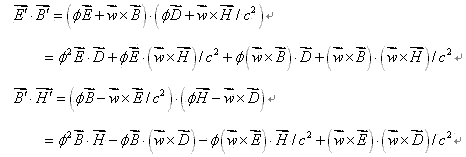
这意味着磁场能量不是场源固有的，而是由电场能量转化而来，有多少磁场能量产生。就必定要有等量的电场能量减少。

4. 动体间的电磁作用力

    运动的场源和观测者其间电磁效应应按观测者静止、场源以等效速度运动情形来讨论。因此，如果观测者携带的检测物体是带有电荷为和载流导线元运动。按照变换后的运动情形，静止的荷电粒子的作用力是

                               (12)

                    (13)

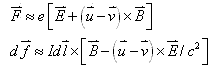(14)

这就是洛仑兹关系式和安培力公式。

    利用(12)、(13)两式计算动体间的电磁作用力时，一定要注意都是观测者相对场源静止时测得的电磁场强度。例如，相对静系分别以速度由于观测者相对可见，一对相对静止的运动电荷间只有静电力作用，并没有磁力作用，这与屈劳顿——诺贝尔电磁实验结果是一致的。再如，相对静系通电螺线管

    在狭义相对论中，经常把观测者相对场源运动时测得场源激发的电磁场场强看做是(14)式中的并认为被作用物体相对观测者可以有不为零的运动速度，按此作法两动体间的电磁作用力是与它们相对观测者运动状态有关。这是极其荒谬的，因为两动体间的电磁作用是唯一的，不可能与两作用物体之外的观测者有关。只有把被作用物体看作是观测者，才能够正确计算动体间的电磁作用力。

3．3 光速的方向效应

者的速度。

5. 结束语

    在经典绝对时空理论框架内，只由麦克斯韦电磁理论是能够解释所有动体电磁实验结果，尤其是那些曾用来探测物体绝对运动的迈克尔逊干涉实验和屈劳顿——诺贝尔电磁实验。并不需要建立狭义相对时空理论。狭义相对时空理论实质上仅是肖氏动体电磁理论的一个特例。

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页