物理科学探疑-网友天空-系统观点-肖军-论电磁波波动方程的协变性
论电磁波波动方程的协变性
肖 军
【摘要】 根据波动方程协变性，在不借助于任何假设情况下，是可以导出电磁波相位不变交换式、光速与光源运动速度关系式以及运动时钟廷缓等结果，由此构筑起来的动体电磁新理论必将取代狭义相对论。
关键词 电磁波 相位不变变换式 光速 动体
在电动力学理论中，解释动体电磁现象用到的洛仑兹变换式是满足不变式
(1)
为了让人相信(1)式是四维时空间隔不变式，爱因斯坦在1905年提出两个基本假设——狭义相对性原理和狭义光速不变假设，并把它们做为支持(1)式成立的理论依据。其实，(1)式的成立与相对论的两个基本假设毫无关系，它并不是什么四维时空不变间隔，更不表示什么相对时空关系，(1)式仅能说明电磁波波动方程的形式与光源运动状态无关。在不引入任何假设条件下，本文利用电磁波波动方程相对光源运动状态具有协变性的结果，不但可以导出(1)式不变式和洛仑兹变换式，还能导出光速与光源运动速度关系式和运动时钟延缓结论。
由于(1)式可以写成形式为
是参照坐标系三维坐标轴正向单位矢量。因此，满足(1)式的变换式应具有形式为
 |
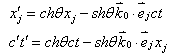(2) |
易验证，波动方程对（2）式变换具有协变形式，即
 |
(3) |
若把其中带撇方程看做是光源运动时辐射光波的波动方程，把不带撇方程看做是光源静止时辐射光波的波动方程。光源在静止和运动两种情形均沿
方向辐射同波数电磁波的两波前应满足
于是，有
(4)
显然，若令
(5)
及
(6)
由(4)式就可得到(1)式不变式。可见，(1)式实际是光源相对静系静止和运动两种情形辐射的两个不同电磁波波振面方程。
满足(1)式的变换式必须具有(2)式的形式，也就是具有形式为
(7)
或者为
但在相对论中，却把(7)错写成形式
看做是空间的第四维，并与三维空间坐标分量相提并论，这肯
这是一个很重要的推论，由它可断定洛仑兹变换式的三维形式不能成立，因为洛仑兹变换式的三维形式虽然满足(1)式不变式，但它不满足(9)式的平行条件。因此。建立在以三维洛仑兹变换为数学基础上的狭义相对论必是错误理论。
由此可把(11—2)式写成形式为
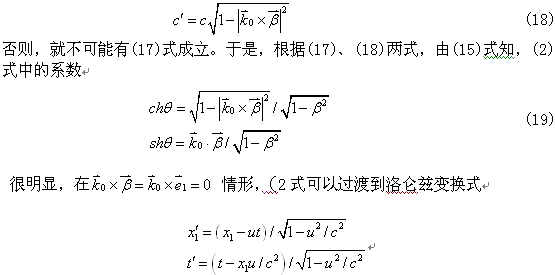
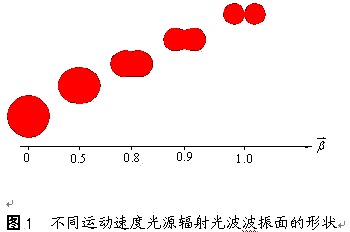
总之，根据波动方程协变性要求，利用麦克斯韦电磁理论解释动体电磁现象是不需要借助于狭义相对性原理和狭义光速不变假设。过去人们把波动方程的协变性看做是支持光速不变假设成立的理论依据，现在知道，这是一种错误的认识，根据波动方程协变性导出的光速是与光源运动速度有关。从(18)式易看出，静止点光源辐射光波波振面是球状，运动点光源辐射光波波振面则是亚铃状，见图1所示。
(18)式是人们梦寐以求的关系式，它的导出将使狭义相对论这座理论大厦失去根基，这本是一件具有划时代意义的事情，但是要想在短期内使人们认识到它的重要性，还存在一定的阻力。除需等待实验进一步验证外，还有就是要克服人们的偏见。列·托尔斯泰曾说过“认识真理的主要障碍不是谬误，而是似是而非的真理”。人们已习惯于用相对论的错误观点思考问题和解决问题，并把这看做是人类智慧的辉煌成就，在这种高唱赞歌的环境下要提出放弃相对论观点，必会招致一些人的盲目抵制和反对，但这并不能阻止人们对真理的追求，事实胜于雄辩，实践会把真理和谬误区别开来，时间也会把一切不真实的东西推向断头台。
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑