物理科学探疑-网友天空-系统观点-肖军-论波动方程对伽利略变换的协变性

论波动方程对伽利略变换的协变性

肖 军

【摘要】本文着重论证了波动方程对伽利略变换也具有协变性。这在现代物理学中必将引起一场突破性的革命，

关键词 波动方程 伽利略变换 协变性

    按照经典绝对时空理论和我们日常经验，相对不同惯性系光波的传播速度是不同的，这本该是毫无争议的结论。可是，在寻找“以太”绝对空间过程中，由于受迈克尔逊——莫雷干涉实验零经果的困扰，以及不能证明波动方程对伽利略变换具有协变性，导致人们不得不放弃经典绝对时空理论，并进而提出狭义相对时空理论。其实，在经典绝对时空理论基础上，不仅完全可以解释迈克尔逊——莫雷干涉实验零结果，也能证明波动方程对伽利略变换具有协变性，根本不需要什么相对时空理论。

    波动方程的协变性是指在一个惯性系中看到的波振面若为球面，在其它惯性系中看到的此波振面也应是球面。这种协变性应当正确的理解为不是要求相对所有惯性系波前的传播速度都恒为c。而是要求波动方程的形式与惯性系的选择无关，这用伽利略变换式是能够给予证明。

    处，并当动系运动至与静系重合瞬间，光源开始辐射光波，根据电磁波的波动方程

(1)

    可知，利用位于静系中的时钟测得在方向上相对静系原

                                   (2)

                             (3)

                                    (4)

    因此，位于静系中的观测者，利用他所携带的时钟（见图１所示）测得波前相对动系原点

                  (5)

    止光源辐射电磁波其波前相对静系的绝对传播速度。相对运动的惯性系而言，

(6)

    为从理论上给出（６）式波动方程，需要知道的另一种表达式。在（５）

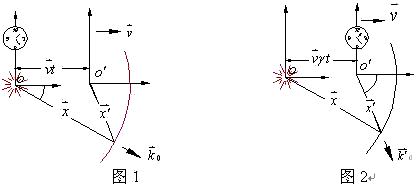
式的导出过程中，是假定观测者位于静系原点其中

                         (7)

考虑到运动时钟延缓效应，在运动观测者所携带的时钟走过时间时，位于静系中的时钟走过的时间应是并有

                                            (8)

传播速度满足经典速度合成公式。

    爱因斯坦要求在任何一个惯性系中看到的波前传播速度都应恒为c，并由此来否定“以太”绝对静止空间的存在，这主要是在推导洛仑兹变换式时，曾做了成一个整体来看待，亦好，利用洛仑兹变换式均能证明波动方程具有协变性。因此，绝不能把洛仑兹变换式看做是支持狭义光速不变假设成立的理论依据，洛仑兹变换实际是（９）、（10）两式在情形时的特例。按照（９）、（10）两式，波前相对动系的传播速度一定是（７）式中的

    （9）、（10）两式也可直接由伽利略变换式导出。但要指出，相对运动的惯性系而言，伽利略变换式的一般形式应为

                 (13)

若注意到

                      (14）

我们就不难导出（9）、（10）两变换式。从而证明（9）、（10）两式与（12）等价，这意味着对（9）、（10）两式协变，对（12）式也一定协变。如果假设光源发光瞬间运动观测者是位于图3所示的o处，类似（9）、（10）两式的的导出过程，利用（7）式我们可以得到场源静止，观测者运动情形时，朝

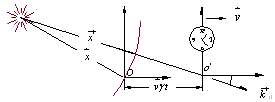
图3

向运动观测者传播的波前有变换式：

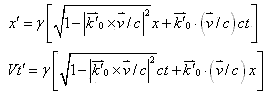（15）

    综上可知，伽利略变换式与波动方程的协变性完全相容。但在相对论中为什么还要否定它呢？这是由于除了错误地认为以及否认波动方程对伽利略变换具有协变性外，还有一个重要原因就是利用（7）式计算迈克尔逊干涉实验结果时，得到的理论结果与实验结果不能相符。其实，导至这种不相符的原因并非是（7）式对光波不能成立，而是以速度运动光源辐射的电磁波其波前相对静系传播速度依据波动方程的形式与光源运动状态无关假设，可导出必须满足

                          （16）

                                （17）

    在经典绝对时空理论基础上，迈克尔逊—莫雷干涉实验的零结果是与（17）相容，这应当看作是支持（17）式成立的实验证据。

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页