物理科学探疑-网友天空-系统观点-肖军-关于麦克斯韦场方程协变性的讨论
关于麦克斯韦场方程协变性的讨论
肖 军
【摘要】本文通过对麦克斯韦场方程协变性的讨论，得出能够使麦克斯韦场方程协变的变换式不只一个，这足以证明狭义相对性原理不能成立。
关键词 麦克斯韦场方程 协变变换 电磁场 狭义相对性原理 光速
我们知道，麦克斯韦场方程
(1)
以及由其导出的电磁波波动方程
 |
(2) |
在洛仑兹变换式的变换下具有协变性。其实，这仅在特殊情形下成立，在一般情形下，真正能使（1）、（2）两式协变的变换式应是肖军变换式
 |
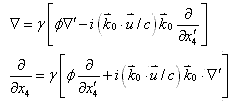(3) |
式中
 |
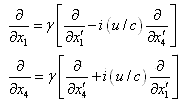(4) |
方向传播的波前，（3）式又可分别化简为
(5)
和
(6)
显然，（4）、（5）、（6）分别是（1）式波前沿三种不同方向传播情形时的变换式。
要求所有的物理定律在（4）、（5）、（6）三式联合变换下具有协变性，这明显是穿凿附会。
事实上，不同的物理定律应有不同的协变变换式。能使牛顿力学定律协变的变换式只能是伽利略变换式；能使（2）式波动方程协变的变换式是（3）式，而能使亥姆霍兹方程
 |
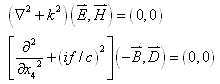(7) |
协变的变换式则是
 |
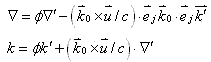(8-1) |
和
 |
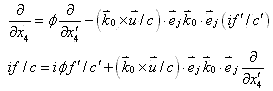(8-2) |
伽利略变换式的不变量是空间间隔，（3）式变换式的不变量是电磁波的波数 ，(8)式变换式的不变量则是相角。
由于（2）、（7）两式均是由（1）式场方程导出，因此可以猜测出，（3）、（8）两变换式也一定都能使（1）式场方程协变，事实的确如此。首先利用能使（7）式方程协变的（8）式变换式对（1）式进行变换，结果有
 |
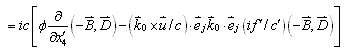(9) |
这一结果可直接由麦克斯韦场方程导出，过程如下：
根据场的散度方程可知
可见，（10）式的成立是不容置疑。由（10）可证
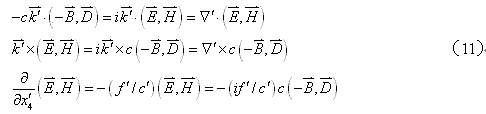
于是，（9）式又能进一步写成形式为
可见，麦克斯韦场方程在（8）式变换下具有协变性。
同理可证，麦克斯韦场方程在（3）式变换下也具有协变性。利用（3）式对（1）式场方程进行变换，有
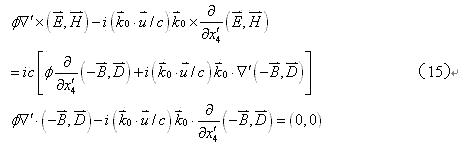
利用（10）式和
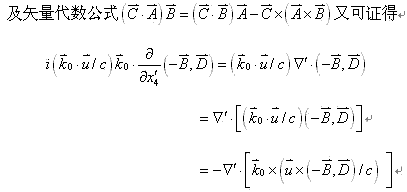
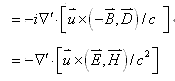
（17-1）
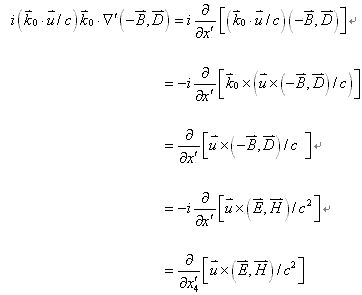(17-2)
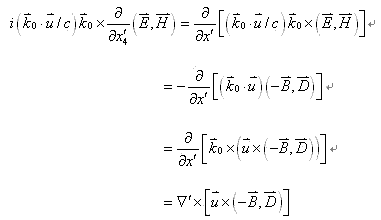(17-3)
很明显，若把（17）式代入（15）式，仍然能够得到（13和（14）式结果。可见，麦克斯韦场方程对（3）式变换也同样具有协变性。
综上可知，（3）、（8）两式都能使麦克斯韦场方程协变，而且由它们所得到的场量变换关系式都是（13）式，这种自洽性意味着理论物理将要重新回到经典绝对时空理论上来。
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑