物理科学探疑-网友天空-系统观点-肖军-关于麦克斯韦场方程相对场源运动状态具有协变性的探讨

关于麦克斯韦场方程相对场源运动状态具有协变性的探讨

肖 军

【摘要】本文依据麦克斯韦场方程组的形式与场源运动状态无关假设，通过对波动方程和亥姆霍兹方程协变性的讨论，确知理论除存在有电磁波相位不变变换式外，还存在有等角变换式。在麦克斯韦电磁理论基础上，利用这两个变换式足以能够解释所有动体电磁现象，并不需要狭义相对论理论。狭义相对论理论的建立，实质是把洛仑兹变换式错当成了本不存在的时空变换式。

关键词 亥姆翟兹方程 动场源 协变性 变换式 电磁场变换方程

    麦克斯韦场方程是19世纪人类最伟大的发现之一，它成功地把电场和磁场统一起来，并预言光波是一种电磁波。在狭义相对论创立之前，用麦克斯韦场方程组解释动体电磁现象需要借助于洛仑兹力和安培力公式，这种理论只能解释场源为低速运动情形时的动体电磁现象。在高速运动情形时，已暴露出许多实验结果与麦克斯韦电磁理论不能相容。笔者经过近20年的研究发现，导致理论与实验不符的原因不是麦克斯韦电磁理论不完备，而是我们在用其解释动体电磁现象时的切入点不对。如果假设麦克斯韦场方程组的形式与场源运动状态无关，在不借助于其它任何假设情况下，由场方程组完全可以解释所有动体电磁实验结果及多普勒效应数学表达式。并不需要狭义相对理论。狭义相对论的建立，反而把动体电磁理论引入歧途。

    麦克斯韦场方程组的形式若与场源运动状态无关，由麦克斯韦场方程组导出的电磁波波动方程和亥姆霍兹方程的形式也应与场源运动状态无关。在文[1]中已讨论过，如果假设电磁波波动方程

                      (1)

因此有

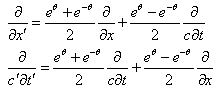(3)

    类似于上述方法，也可得到使亥姆霍兹方程协变的变换式。所谓亥姆霍兹方程，就是仅依赖于空间坐标的振幅方程

由此能够得到

    这是一个与(3)式同等重要的变换式，我们不妨称其为等角变换式，利用它可以很容易导出电磁场的变换方程。

    调和函数，就必有

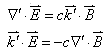                                                   (14)

    （14）式也可由麦克斯韦场方程导出，根据麦克斯韦场方程可知

由(13)式和(14)式可证

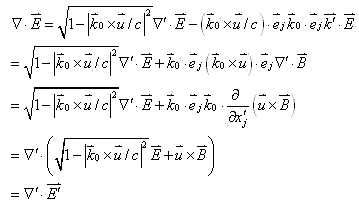
及

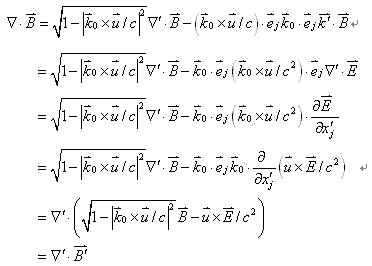
也即有电磁场变换方程

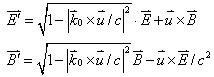（15）

在文[3]中，利用变换式(3)也曾得到(15)式结果。并对其做过详细的讨论，限于篇幅，这里就不再赘述。

式(16)的导出并不难，由于(3)式中的

    把(12)式代人(20)式，同样也可导出(16)式结果。

    以上就是我们根据场方程的协变性导出的部分结论。麦克斯韦在建立场方程组时，并没有考虑场方程组的协变性。爱因斯坦虽然考虑了场方程组的协变性，但是。他没有把这种协变性看做是相对场源运动状态，而是把它错看成是相对于惯性系，且从坐标变换角度人手，根据一些不实假设导出满足波动方程协变性的坐标变换式是洛仑兹变抉式。从前述的（3）式知道，洛仑兹变换式的形式是正确的，但它不是两惯性系间的坐标变换式，而是电磁波周相不变变换情形时的一个特例。

     爱因斯坦关于洛仑兹变换式的导出犯有严重的逻辑错误，他是依据虚假的前题，用错误的论证方法，才导出正确的洛仑兹变换式，并将这正确的变换式视为支持虚假前题成立的理论依据。假如他的前题是正确的。或者推导过程无问题，按照他的方式不可能证得两惯性系间的坐标变换式是洛仑兹变换式。仅有在经典绝对时空理论基础上，依据笔者提出的“麦克斯韦场方程组的形式与场源运动状态无关”假设来讨论麦克斯韦方程的协变性，才能够得到正确的动体电磁理论。

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页