物理科学探疑-网友天空-系统观点-夏烆光 -狭义时空与爱因斯坦相对论的联系
![]()
狭义时空与爱因斯坦相对论的联系
(撰文:夏烆光)
注意到接触作用原则和相互作用传播速度的有限性,本文指出:在物理学中,人们首先面临的是:把“几何学”作为“物理学”的工具的可能性问题。正如所知,几何学本身是人们对于现存空间关系的一种抽象,是绝对瞬时性的空间关系的一种数学表示。那么,这种瞬时性的几何抽象能否无条件地、绝对正确地表象客观事物在运动过程中所形成的空间关系和运动规律,即物理学的运动规律呢?或者说,在物理学中,利用相对速度乘以时间(V·t)得到的“运动距离”能否用抽象的几何线段来无条件地、精确地加以表示呢?本文的回答:这是根本不可能的!!因为,在现行的几何学中,无论是欧几里德几何、还是罗巴切夫斯基几何、亦或是黎曼几何,它们使用的几何线段——抽象的空间关系——都是建立在绝对瞬时性的时间观念之上,在所形成的几何线段两个“端点”之间,都具有“绝对瞬时性”。因此,这种意义上的空间乃是“惯性空间”,或者说是“欧几里德空间”。从时空的属性上来区分,我们不妨把这种时空叫做“狭义时空”。这里,我们讨论了“狭义时空”上成立的相对论,并把它叫做“狭义时空相对论”。通过整个讨论可以看出,《狭义时空相对论》与爱因斯坦的《狭义相对论》之间,在本质上是完全相同的。而《狭义时空相对论》只能建立在物体运动的“绝对速度”介于光速和无穷大之间(c<υ<∞)的前提下才能成立。事实上,这是根本不可能的。所以说,爱因斯坦的狭义相对论也是根本不正确的。
一 引 言
正如上述,考虑到光速传播有限性的影响,在物理学中,人们所面临的一个重要的问题是:通常的关于空间关系的几何抽象能否无条件地、绝对正确地表象客观事物在运动过程中所形成的空间关系和规律性?或者说,利用速度乘以时间(V ·t)所得出的“运动距离”究竟能否无条件地用抽象的几何线段来精确地加以表示?这里的回答是:从严格地意义上来说,这种表示是根本不可能的!!因为,在现行的几何学中,无论是欧几里德几何,还是罗巴切夫斯基几何,亦或是黎曼几何,所使用的几何线段——抽象的空间关系,都是建立在绝对瞬时性的时间观念之上。换句话说,针对一个运动质点所形成的空间距离(几何线段)来说,人们在几何抽象时,从来没有过问在信号传播速度有限性的影响下,这一几何线段在形成的过程中,它的起点和终点,在时间坐标上与绝对同时性时间观念的关联。不难理解,只要忽略了这一偏差,就等于在无形之中承认:信号的传播速度是无穷大,同时性是绝对的。所以说,任何几何抽象在本质上都没有摆脱绝对瞬时性的时间观念。
的确,单纯从逻辑推理的几何研究出发,我们也可以把由于运动所形成的空间距离——抽象的几何线段——建立在绝对同时性的时间观念之上。这样一来,在所形成的几何线段的两个“端点”之间,便具有绝对同时性。显然,这种意义上所形成的空间乃是“惯性空间”,或者说,是“欧几里德空间”。按照这种几何抽象所形成的空间关系的几何理论,只能适用于在惯性空间上所讨论的物理问题,包括在惯性空间中成立的爱因斯坦狭义相对论。当然,如果从时空概念的属性上来区分,也可以把这种惯性空间叫做“狭义时空”,把狭义时空上成立的相对论叫做“狭义时空相对论”。其实,把话说白了,“狭义时空相对论”就是爱因斯坦的“狭义相对论”。为了便于理解,这里我们还是采用对话的方式来加以介绍。
二 狭义时空相对论问答
问:什么是狭义时空?
答:“狭义”一词是相对于“广义”而言。“狭义时空”也就是“惯性时空”。因为在惯性时空上“时钟”只有一个,“同时性”是绝对的,所以我们把它称为“狭义时空”。
问:这种时空上的相对性是什么意思?
答:在这种时空上的“相对性”纯粹与观测者(主体)观测问题的角度有关,而与“光速有限性”毫不相关。也就是说,由于观测者所处的位置各不相同,对于同一个客观事件照样会得出完全不同的观测结果。因为,在这种情况下,一切客观事物都处在绝对静止的状态下、整个宇宙只有一个统一的时钟来记录时间过程的变化。事实上,客观上并不存在绝对静止的事物,宇宙中也根本没有统一的时钟!显而易见,这是一种理想化的、纯粹的、抽象的空间关系。不过,人们在认识世界的时候,总是需要通过观测和抽象来形成概念。正所谓:“君子居则观其象而玩其辞,动则观其变而玩其占。”(参见《易经·系传》,第464页)
问:静止状态的相对性又意味着什么?
答:如果事件处于所谓的静止状态,情况就大不相同。在静止的状态下,如果继续用四度坐标来表示两个事件的时空间隔(Δs),就是空间关系的纯粹的几何抽象。其实,由这种抽象的空间关系演绎的几何理论,就是熟知的《欧几里德几何学》。因为,欧几里德几何学也是在绝对同时性的时空观念下,对静止事物之间的“空间关系”所做的数学抽象。不难看出,在这种情况下,两个“世界点”的第四度坐标t1和 t2便具有共同的时间起点(t0),于是,t1和 t2 就变成同一个时钟的不同时刻。参见下图。
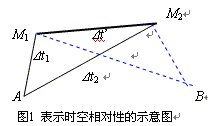
在上图中,我们令:Δt’=t’2–t’1,Δt1=t1–t0,Δt2=t2 – t0,则光速c和时间间隔Δt的乘积:cΔt’、cΔt1以及cΔt2就是欧几里德平面上的三条直线。由这三条直线所构成的平面三角形(AM1M2)必定满足欧几里德几何的一般定理,譬如,任意三角形的两边之和大于第三边,即:
Δs = c (t2 – t1) –Δr ≤ 0. (1)
这时,尽管不同的观测者A,B,C,…之间,对应着不同的时间间隔ΔtA=Δt2 –Δt1,及ΔtB,ΔtC,…,并构成一系列不同的虚拟时空间隔Δs0,Δs1,Δs2,…,但导致这种相对性的原因已经不是信号传播速度的有限性了,而纯粹是由于主体(观测者)观测问题的角度不同所带来的主观性。这种主观性,就是狭义时空相对论的讨论内容。
问:这时又怎样地定义时空间隔呢?
答:用光速c和虚拟的时间间隔Δtn的乘积(cΔtn)表示事件的空间距离,这时,“虚拟时空间隔”可写成:
Δs0 = (Δr’2 – c2Δt’2)1/2 = 0, (2)
以及,
Δsn = (Δrn2 – c2Δtn2)1/2 ≥ 0. (3)
在这里,由于Δrn2 ≥c2Δtn2,所以有Δsn≥0. 再由于Δrn≡Δr’,所以有Δt’ ≥Δtn. 其中,n = 1,2,3,…代表着不同的观测位置。
问:这时的时空间隔又有什么意义?
答:这时的时空间隔Δsn仍然是不同观测者对同一客观事件观测结果的相对性,是事件处于静止状态、且不受光速有限性影响下的相对性,是纯粹由于主体观测问题的角度不同所带来的主观性。
问:在这种情况下的间隔相等的根据又是什么呢?
答:照样根据“客观性原理”,而不是“光速不变原理”。因为,尽管光速有限性已经不是这种时空间隔可变性的客观原因,但在给定的数学形式下,间隔相等的命题也不成立。
问:为什么这样说呢?
答:首先,即使同在惯性时空中,不同的时空间隔照样对应着不同的观测者。对于这些分明不相等的时空间隔,强令它们相等是既不符“形式逻辑”,也不符合“数学抽象”。但是这些不相等的“世界线”纯粹是由于主体观测角度的不同而造成的,实际上是相等的。这就如同罗巴切夫斯基几何的直观意义一样:分明是一些“不相等的线段”,在一种使用着不相等的“度量单位”的测量法则下,却可以认为它们都是“相等”一样。或者说,在圆内(或球内)几何中,却可以认为它们都是相等的一样。(详见[1],§44节)
问:这时的客观性原理可以用数学方法加以证明吗?
答:同广义时空相对论的情况一样,也是不可以证明的。其道理也相同。
问:在Δt’≥Δtn时,它们之间的相互关系又是怎样?
答:当我们令:Δt’ = t2 ’– t1’,Δtn =Δtn2 –Δtn1时,cΔt’ 就代表从起点到终点两个事件(即数学点)之间的距离,而cΔtn就代表两个数学点与同一个观测者之间的空间距离之差,而在欧几里德几何中,任意三角形的两边之差必定小于第三边。考虑到它们都是以光速作为度量单位,所以必定有Δtn≤Δt’.
问:如何求得Δtn和Δt’的相互关系?
答:根据客观性原理,我们可以利用(2)和(3)式写出:
(Δrn2
– c2Δtn2)1/2 ≡ (Δr’2 – c2Δt’2)1/2.
(4)
这里的时间间隔Δtn和Δt’ 都是虚拟的,所谓的“运动”也是虚构的。类似于广义时空相对论的推导:站在运动事件上的观测者,当他以运动事件为参照物时自己是静止的,即Δr’= 0,由此得出:
Δtn=Δt’/(1 – Vn2/c2)1/2. (5)
或者记做
t = t’/(1 – V2/c2)1/2. (5’)
这就是狭义时空相对论虚拟时间间隔之间的变换公式。
问:这个变换有什么物理意义?
答:所设Vn2 =Δrn2/Δtn2,而Vn是站在运动事件外的观测者所使用的“虚拟相对速度”。由于Δt’ ≥Δtn,所以有:|Vn |≥c. 由此可见,虚拟时间间隔Δtn及虚拟相对速度V n都是虚数。因此说,这种变换并没有实际的物理意义。此外,因为在任何位置上(4)式均能够成立,所以省去了下脚标,而把Vn=Δrn/Δtn写作V =Δr/Δt.
问:这个时间间隔有什么意义?
答:由于变换是在狭义时空之中进行的,所以这个时间间隔Δt代表了任意两个事件之间虚拟时间过程的相对比较。
问:这又有什么实际的物理意义呢?
答:它的物理意义是:位于事件之中的观测者,总是觉得自己周围事物的时间过程流逝的比其它位置上同样事物的时间过程都慢一些。极端的情况下,感觉时间慢地将停止流逝。
问:如果以任何虚拟的均匀速度表示距离情况如何?
答:如果我们是以某个虚拟的相对速度V与虚构的时间间隔Δt的乘积来表示空间距离Δr的话,那末,V=Δr/Δt就是站在事件以外的观测者所感受到事件的“虚拟相对速度”;而Δr’ 与Δt’的比值υ=Δr’/Δt’ 就是事件上的观测者“虚拟的绝对速度”。在客观上,由于Δr≡Δr’,所以VΔt ≡ υΔt’. 根据(5)式便可以导出:
υ= V/(1– V2/c2)1/2. (6)
这个公式是在狭义时空中,任意两个事件的虚拟速度之间的变换公式。由于V≥c,所以,当虚拟的相对速度V 由 c → ∞ 时,则虚拟的绝对速度υ 由∞→c。
问:这又有什么实际意义呢?
答:这就意味着:站在事物之上感觉事物的“绝对速度”总是比站在事物之外任何位置上都快一些。极端的情况,V = c,则υ= ∞,二者之间便没有相对论意义上的任何变化了。
问:这时的空间关系又可以写成什么样的形式呢?
答:可以写成:
L = L0(1–V2/c2)1/2. (7)
这个公式表明了在狭义时空中,任意两个事件之间空间距离的相对性。由于V≥c,所以这个空间距离L也是虚数。当V=c时,则有L = 0。
问:空间距离是虚数又有什么实际意义呢?
答:位于事件之上的观测者观测该事物的“映象”的空间尺度趋近于零,任何空间尺度都集中于一个点,空间概念失去了物理意义。显然,上述所列的感觉都是虚幻的。一句话,狭义时空相对论仅反映了主体从不同的位置上对于同一个客观事物(客体)的映象观测结果的相对性,而不代表客体本身的时空尺度及其相对速度等物理量真地有任何实质性的变化。不难看出,这种情况犹如“仿射几何”一样。——因为,这种变换只保留了图形的某些性质,其中包括:图形的“射影性质”以及其它的一些仿射性质等。
总而言之,在绝对同时性的基础上,也可以建立相对论。不过,由于这种相对论是建立在绝对同时性的惯性时空之上,所以仅具有抽象的物理意义。它所表现的运动规律并不是物质的真实运动规律,而是它的抽象运动规律。也就是说,它所反映地仅仅是射影几何和仿射几何所形成的空间关系。所以,狭义时空相对论应是此类几何学科的理论基础。
三 罗巴切夫斯基几何的时空观念
1、罗巴切夫斯基几何意义的相等
罗巴切夫斯基圆内(平面)几何和球内(空间)几何的前提是:明明在欧几里德空间中是不相等的“分割”(即线段),在圆内或球内,却可以认为相等。但是,这种几何的物理基础是什么?在迄今的数学领域里还没有作出明确地回答。为了说明罗巴切夫斯基几何的物理基础,读者需要参见[1]的第五章§36节。在那里,我们已经清楚地指出:罗巴切夫斯基假设线段AB处在弦CD上,并且约定不包括弦CD和圆的边界相交的两个端点C和D在内,参见下图)。
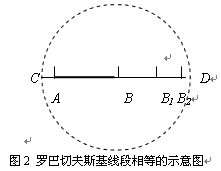
然后用普通测量长度的法则所组成的复合比值(CB/CA :DB/DA)的对数值,即:
log[(CB/CA)/(DB/DA)]=log CB–log CA–log DB+log DA. (8)
作为“测量单位”,来测量弦CD的长度。按照这种定义选择长度单位的测量法则,将使图中的弦CD有了无限长度。也就是说,在普通的意义下只有有限的长度,而在罗巴切夫斯基几何中,由这条弦CD所表达的直线却有无限的长度。
表面上看来,这种说法是自相矛盾的!但是按照罗巴切夫斯基几何的有关定理,它是无矛盾的。这是因为,如果我们用了取作移动的变换,线段AB变成了线段BB1,再变成B1B2,等等,则得到的线段在普通的意义下,将变得越来越短。但是,由于罗巴切夫斯基几何已经事先约定CD的端点除外,并且由这些点所截取的线段,都是“相等的”。所以在罗巴切夫斯基几何意义下,这就意味着端点在“无穷远”。即这些点B,B1,B2,…,Bn,…并非越来越密,而是趋向无穷远。可以证明,运用(8)式进行的移动变换,一个接一个地截取“相等”的线段,决不会从圆内跑到圆外。通过这样的移动变换,最后,坐标为xn的点Bn变成坐标为
xn+1 =(xn + a)/(1 + axn) (9)
的点Bn+1。由此可知:
x0 = a, x1=2a/(1+a2),x2 = (3a+a3)/(1+3a2),… (10)
由于所有线段BnBn+1都是经过表达移动的变换而得到的。所以它们彼此都相等,即:
AB=BB1,BB1 = B1B2,B1B2 = B2B3 ,…,Bn-1Bn = BnBn+1…. (11)
这就是罗巴切夫斯基几何意义下的相等。点Bn 向着直径的端点越来越密。但在罗巴切夫斯基几何下,直径的端点趋向无穷远,而不是线段越来越密。这是迄今为止数学领域对罗巴切夫斯基几何所做的唯一解释。这表明迄今的数学尚未认识到这种相等的物理本质。
2、罗巴切夫斯基几何的物理基础
把空间线段写成:
Li = L0(1– Vi2 /c2)1/2, (12)
显然,对于一系列的相对速度Vi(i = 1,2,3,……),可以求出一系列的Li 。如果把这些结果人为地集合,那末Li就和dsi一样,也会构成一种空间(L),即:
![]() (13)
(13)
应该看到,这个集合上的每个线段Li都不相等。但是,这种不相等是主体对客体观测结果的相对性,是主体观测位置的改变引起的。从本质上讲,它们是同一个客观事物,因而是不会因观测位置地改变而随意地改变,否则将不再有客观真理!!也就是说,“客体应有不依赖于主体的客观内容”这一点是个“客观真理”。不管时空间隔看上去是大还是小,客观上都是一样的。显然,这种“相等”和罗巴切夫斯基几何意义上的“相等”是完全一样的。所以说:罗巴切夫斯基几何意义上的“相等”乃是“客观性原理”的直接推论。
3、时空间隔不变与光速不变原理无关
在狭义时空之中,时空间隔平方的可以定义为:
s2 = r2 – c2(t22 – t12)。 (14)
如果我们令线段:
BM12 = c2(t2 – t1)2, (15)
则(14)式可改写成:
s2 + BM12 = r2, (16)
显然,(16)式是以r为弦、以s和BM1为两条直角边的“勾股弦定理”,——西方人称之为“毕达哥拉斯定理”。对于(16)式,我们可以利用弦r为直径作圆,并分别用sA,sA1,sA…及BM1,B1M1,B2M1…为两条直角边作若干个圆内接三角形。
然后再分别用线段M2A,M2A1,M2A2,…在直径M1M2上对应地截取相等的线段M2A’,M2A1’,M2A2’,…,同时,我们利用sA2 = M2A2、sA12 = M2A12、sA22 = M2A22…等来代表时空间隔平方。这样一来,便可以写出:
M1A2 = c2(tA2–tA1)2,M1A12= c2(tA12–tA11)2,M1A22= c2(tA22–tA21)2. (17)
并且我们可以写出:
sA2 =M2A2 =M2M12– c2(tA2– tA1)2,sA12=M2A12=M2M12– c2(tA12–tA11)2,
sA22=M2A22=M2M12– c2(tA22–tA21)2. (18)
由此得出如下图形:
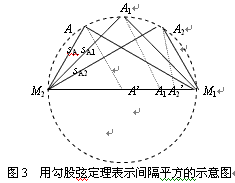
由上图可以明显地看出,即使已经使用了光速不变原理,仍有:
M2A’≠ M2A1’≠ M2A2’ ≠… ≠ M2An’ …, (19)
这也就证明了时空间隔不变与光速不变原理无关。所以说,光速不变原理根本不是时空间隔不变的物理基础。
4、罗巴切夫斯基几何平行公理与客观性原理
下面,我们用数学方法证明,在客观性原理基础上的相等与罗巴切夫斯基几何意义上的相等是一样的。进而证明:罗巴切夫斯基几何意义上的相等是客观性原理的直接推论。证明这一点,就是证明(11)式所代表的相等,同在客观性原理的基础上,人为地把(19)式写成相等的形式是一样的。即勒令:
M2A’= M 2A1’ = M2A2’ = …= M2An’…, (20)
所构成的(20)式,与(11)式的物理意义是相同的。为了方便,我们从(19)式出发,来证明它与(11)式所代表的相等是一样的。从图3我们可以得到:
A’A1’ = M2A1’- M2A’
…①
A1’A2’= M2A2’- M2A1’
…②
(21)
A2’A3’= M2A3’- M2A2’
…③
用① 减②得:
A’A1’- A1’A2’ = 2M2A1’- M2A’- M2A2,
用②减③得:
A1’A2’- A2’A3’ = 2M2A2’- M2A1’- M2A3’,
由(19)式可以得到:
AA1’- A1’A2’ = 0;A1’A2’- A2’A3’ = 0;… , (22)
故有:
A’A1’ = A1’A3’;… A’n-1An’ = An’A’n+1… . (23)
显然,上式与(11)式的相等是完全一样的。这就证明了罗巴切夫斯基几何意义下的相等,与客观性原理所给出的相等,在物理意义上是相同的。所以说,罗巴切夫斯基几何的相等,是客观性原理的直接推论。客观性原理本身反映的是主体(观测者)对于客观存在的事物观测结果的相对性,与客体(客观事物)本身存在形式(空—时坐标)之间的辩证关系。由此可见,罗巴切夫斯基“平行公理”与欧几里德“平行公理”(参见[2]第127页)的区别仅在于:前者反映的是时空观测结果的相对性(是有条件的);后者反映的是时空代表着物质存在形式的绝对性(客观实在性)。而客观性原理,则是两者之间相互联系的桥梁!
5、在客观性原理之上的绝对同时性
下面,我们用另一种表达方式来证明在客观性原理之上的“绝对同时性”。 参见下图:
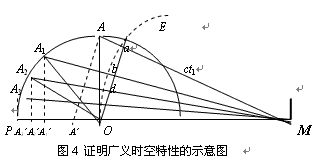
其中,点M为一观测者的观测位置,OA为一长度等于L0、并绕固定的点O逆时针旋转的直线。显然,在惯性参考系中,这个相对速度就等于物体的运动速度。但是,在“狭义时空”中它就是两个惯性参考系之间的“相对速度”。我们在圆弧PA上任意地取出点A,A1,A2,A3,…,这些点都可以看成是M点绕O点的逆时针移动时,与观测者观测位置的对应点。再以M点为圆心、以MO为半径划一圆弧线OE,分别与线段MA,MA1,MA2,… 等相交于a,b,d,… 各点。然后,通过A,A1,A2,A3,…各点做OE弧的弦Oa,Ob,Od,… 的平行线,分别地与线段OP相交于A’,A1’,A2’,A3’,… 等各点。根据上图,我们可以由欧几里德几何关系得出:
OA’ = aA,OA1’ = bA1,OA2’ = A2d,…, (24)
用光速c与时间t的乘积代表上图中有关线段的长度。那么,我们根据绝对速度不变这一“光速不变原理”得出:
MO=Ma= Mb=Md= … = ct1…. (25)
再令:MA= ct2A,MA1= ct2A1,MA2= ct2A2,…,我们便可以得出:
aA=MA–Ma= c(t2A–t1),bA1=MA1–Mb= c(t2A1–t1),A2d =MA2–Md = c(t2A2–t1). (26)
根据时空间隔的定义和“相对性原理”,并注意到OA,OA1,OA2,OA3 …是圆弧PA的半径,它们是相等的,那末我们利用上式,在不同坐标系中写出时空间隔平方为:
S2A=OA2–aA2= OA2–c2(t2A–t1)2,S2A1=OA12–bA12= OA2–c2(t2A1–t1)2,
S2A2=OA22–dA22=OA2– c2(t2A2–t1)2. (27)
根据客观性原理:
S2A=S2A1=S2A2= …, (28)
由(27)式得:
aA2 = bA12 = A2d2 = …, (29)
以及,
c2t2A2 = c2t2A12
= c2t2A22 = ….
(30)
再由光速不变原理得:
t2A = t2A1 = t2A2 = …. (31)
这一结果表明,在客观性原理之上,所有的时间坐标都是相等的。
除此之外,由于线元平方
ds = (dx2 +
dy2 + dz2 – c2dt2)1/2
(33)
是一条曲线,所以“狭义时空”与“罗巴切夫斯基空间”一样,也是弯曲的。当然了,这种弯曲纯粹是由于人们的主观表象造成的,而并非是现实的空间真的在那里弯曲的摆放着。
总而言之,在惯性时空中,时间具有绝对瞬时性。在绝对瞬时性的时间观念下成立的相对论几何是罗巴切夫斯基几何。从本质上来说,罗巴切夫斯基几何意义上的相等是客观性原理的直接推论,而罗巴切夫斯基几何的物理基础是相互作用传播速度的有限性。由于罗巴切夫斯基几何是在绝对速度大于光速的条件下成立的。而绝对速度大于光速的物质是根本不存在的,所以说,罗巴切夫斯基几何根本没有物质基础。
四 狭义时空与爱因斯坦相对论的联系
诚如所知,爱因斯坦的相对论在使用的物理量、物理概念、和物理原理中,总是利用自己头脑的抽象思维,而没有考虑在相互作用传递速度有限性和接触作用原则基础上,所导致的时间坐标的滞后(没有包括?t),因而,没有从根本上摆脱绝对同时性的时间观念。而“狭义时空相对论”正是从这种意义上出发来考虑问题,——即从牛顿力学的意义出发,来建立“间隔相等”的物理观念。因此,从本质上来说,“狭义时空相对论”与爱因斯坦的“狭义相对论”并没有本质上的区别。因为,这两者之间,在确定静止系的时间坐标上,都是忽略了传递运动信息所需要的时间过程(△t)。
为了便于理解,这里再把“间隔平方”的定义,作进一步的说明。
1、间隔平方本身究竟是直线性的还是非直线性的对于坐标变换无关紧要
在广义时空相对论中,线元平方(间隔平方)究竟是曲线还是直线与相对论问题毫不相关。因为,相对论是:相对运动观测者站在运动事件上,使用运动时钟来记录“时间过程”;相对静止观测者站在运动事件的起点上,使用静止时钟来记录同一个运动的“时间过程”。然后,“我们”利用自己的理性思维,把两个坐标系上的观测者所得出地“时空变量”加以比较(坐标变换)。在相对运动的两个观测者之间,不管这个运动是直线还是曲线,也不管这个运动是加速的还是匀速的,所形成的空间距离对于分别站在这一距离两个端点上的观测者来说,永远是同一个物理量,即r ≡ r’。为了明确起见,我们把牛顿力学、狭义相对论、广义时空相对论等,列表加以比较。
| 狭义相对论 | 广义相对论 | 广义时空相对论 |
| 空间是平坦的 | 空间是弯曲的 | 空间没有几何性质 |
| 空间、时间的可变性是真实的 | 空间、时间的可变性是真实的 | 空间、时间的可变性是辩证的 |
| 空间与时间是近似可分的 | 空间与时间是绝对不可分的 | 空间与时间是绝对可分的 |
| ds2≈c2dt2-dx2-dy2-dz2 | -ds2 = gikdxidxk | ds2=c2dt2-dx2-dy2-dz2 |
| 运动系与静止系完全独立, 坐标变量间没有共同的起点 |
运动系与静止系并非完全独立,但是坐标变量间却没有共同的起点 | 运动系与静止系并非完全独立, 坐标变量有共同的起点 |
| 不同的坐标系度规是不同的 | 同一个坐标系度规是不同一的 | 不同的坐标系度规是同一的 |
| 以相对性原理为前提对坐标变量进行变换(ds2 ≈ds’2) | 以方程协变性为前提对坐标变量进行变换:选出形式不变的物理方程 | 以客观性原理为前提对坐标变量进行变换(ds2 ≡ ds’2) |
| 不考虑静止系时间坐标t中所包含的滞后过程 | 考虑到静止系时间坐标t中所包括的滞后过程 |
2、三种几何学的相互比较
诚如上述,利用广义时空相对论的时空观念,我们初步地创立了一门新的几何学原理,我把这种几何学叫做《广义时空几何原理》。现将欧几里德几何、黎曼几何(或罗巴切夫斯基几何)、广义时空几何的基本要点比较如下:
| 欧几里德几何 | 黎曼几何 | 广义时空几何 |
| 时空的几何性质是平坦的 | 时空的几何性质是弯曲的,与罗巴切夫斯基几何类似 | 时空根本没有几何性质 |
| 牛顿力学在其中成立 | 广义相对论在其中成立 | 广义时空相对论在其中成立 |
| 时间和空间是绝对不变的,度规是刚性的 | 时间和空间的可变性是真实的,度规是可变的 | 时间和空间的可变性是相对的,度规是刚性的 |
| 站在运动事件之上、用运动时钟,对处于静止状态的物体抽象出来的时空。在这种时空中有:υ= 0. 以及,相对性系数:ξ= 1. | 站在运动事件之外、用静止时钟对介于光速和无穷大的绝对速度之间状态的物体抽象出来的时空。这种时空中有:c
<υ<∞,以及相对性系数:O < ξ< |
站在运动事件之外、用静止时钟对介于光速和无穷大绝对速度之间状态的物体抽象出来的时空,这种时空中有:0<υ≤c,以及相对性系数: |
| 有物质基础 | 没有物质基础 | 有物质基础 |
可以说,通过广义时空相对论的时空观念,不仅可以清楚地阐明《广义时空几何学》、《欧几里德几何学》、以及《罗巴切夫斯基几何学》(包括《黎曼几何学》)之间的相互关系,而且还可以指出各种几何学成立的“物质基础”。除此之外,从“绝对瞬时性”的时间观念出发,我们又建立了一种全新的相对论,并把它叫做《狭义时空相对论》。这一时空理论与爱因斯坦的狭义相对论在本质上是完全相同的。它们都是在静止系的时间坐标中忽略了滞后的时间过程。
五 结 论
总之,通过以上的讨论,不仅可以清楚地证明爱因斯坦的狭义相对论并没有摆脱绝对同时性的时间观念,而且还可以清楚地证明:传统的几何理论也是建立在绝对同时性的时间观念之上。因此说,几何的抽象只有在纯粹的几何学中才是无条件地有效的。正因为这样,所以在现代物理学中,在必须考虑到相互作用传递速度有限性的场合下,注意到接触作用原则后,必须在静止系的时间坐标中,包括进去传递运动信息所需的滞后的时间过程。注意到这个过程的相对论,就是《广义时空相对论》,忽略了这个滞后的时间过程的相对论,就是《狭义时空相对论》。而爱因斯坦的相对论,也是在忽略了这个滞后的时间过程中导出的,所以说,爱因斯坦的《狭义相对论》与《狭义时空相对论》之间,并没有本质的区别。由于狭义时空相对论的导出条件,相当于信号的传递速度介于光速和无穷大之间,而这种要求本身并没有物质基础,所以说,狭义时空相对论并不是一个描述物体真实运动规律的物理理论。同样的道理,爱因斯坦的狭义相对论也不是描述物体真实运动过程的物理理论。因此说,我们决不应该根据爱因斯坦相对论所取得的巨大成就,来掩盖这一理论本身的逻辑谬误和概念错误。
事实证明,以恩格斯的自然辩证法为基础所建立的广义时空相对论,无论的逻辑的合理性上,还是在实际应用中,都是一个比爱因斯坦的狭义相对论和广义相对论都更加正确的时空理论。它不仅可以解决爱因斯坦的相对论已经解决的时空问题,而且可以解决爱因斯坦的相对论一直无法解决的时空问题。因此,我们可以坦率地说:广义时空相对论的创立,为现代物理学、现代数学、现代宇宙学、以及现代自然哲学的研究与发展,提供了前所未有的理论基础。
参考文献
[1] 《广义时空相对论》夏烆光著,北京,人民交通出版社,2003年1月第一版。
[2]《数学—它的内容、方法和意义—》[苏] А.Д.亚历山大洛夫等
编著,王元、万哲先、
裘光明 等译,第三册,科学普及出版社,1962年5月第一版。
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑