物理科学探疑-网友天空-系统观点-夏烆光 -广义时空几何学原理

广义时空几何学原理[1]

（撰文：夏烆光）

这里介绍的是一种全新的几何理论。可以说，这种几何理论为“广义时空相对论”提供了有力的数学依据。或者更确切地说，广义时空相对论为这种几何学提供了可靠的物理基础。通过广义时空相对论的物理实践证明，这一几何原理不仅可以解决现代物理学中各种已知的时空问题，而且可以用于解决现有理论无法解决的时空问题。特别是，这里所证明的“存在着一种没有因果规律的时空”的结论，确实是有些骇人听闻！！但这是逻辑推理的必然结果。——当然，这个结论必须建立在：所有以光速运动的物质将构成一个“统一的、连续的、不可分割的整体”这一前提下。可以预见，这一几何理论对现代数学、现代物理学以及现代哲学的研究与发展，将产生深远的影响。

一    广义时空几何观念的形成

    我们说，无论是那种几何学，都是关于空间关系的抽象。而在宇宙中，空间关系的形成，可以分为两类：第一类，是物质世界固有的空间关系——是静态的空间关系。例如，有形物体的几何图形与尺寸的相互关系；第二类，是物质运动所形成的空间关系——是动态的空间关系。例如，“质点”运动时所形成的各种空间距离及其相互关系。对于前者的抽象，并不需要考虑光速传播有限性的影响，而对于后者，又不得不考虑光速传播有限性的影响。

    在几何学的抽象中，通常，人们总是同时地面对着各种几何线段的“起点”和“终点”。同时地面对着各种线段起点和终点的几何学，是建立在不考虑相互作用传播速度有限性影响这一类空间关系的前提下。所以说，现有的各种几何学原理都是建立在几何线段的起点和终点之间具有绝对同时性的时空观念的基础上。或者说，都是属于静态空间关系的几何抽象。

    我们的原则是：那些能够通过你的“想象”而形成某种概念，但按其本质来说却是不能付诸于实践的东西——纯粹的理念——例如不同地点上的时钟之间的“同时性”问题，都没有确切的物理意义。所以说，在相互作用传播速度有限性的影响下，不仅“惯性时空”的概念失去了严格的物理意义，而且在几何学中，关于“线段”的概念也失去了严格的物理意义。因为在几何的抽象中，用“线段”来代表一个质点的相对运动所形成的“空间距离”时并没有考虑到这个空间距离两个端点在时间上的绝对不同时性。

    所以说，现有的几何学并不适用于来自于质点运动时所形成的空间关系。于是，就产生了建立一种适合于物质运动所形成的空间关系的几何学的新思想。这种几何学原理，就是我们随后将要讨论的广义时空几何学原理。具体地说，广义时空几何学原理，是在广义时空相对论的基础上，抽象出来的一种新的几何学。按照广义时空相对论的观点：同时性的相对性是来自于相互作用传播速度的有限性。在这种观点下的时空观念，不仅与赝欧几里德空间（即伽利略的惯性时空）上洛伦兹群的移动变换不同，而且与罗巴切夫斯基几何（或黎曼几何）的时空观念也不同。

    的确，从“度量空间”和“拓扑空间”的角度上来看，距离的概念既可以由欧几里德空间上的点与点之间的“线段”来引入，也可以由n维空间上的“世界点”与“世界点”之间的间隔来引入。但是，不管距离是怎样地引入，只要有移动存在就一定存在两个点在时间上的先与后。然而，自古以来，数学的抽象总是用绝对同时性的“抽象思维”来描述物理对象。——所有从事数学抽象的观测者总是绝对同时地站在两个不同的观测位置上来考虑同一个物理问题，从来没有人去过问在一个原始物理点与它的移动所形成的新物理点之间，由于光速传播有限性的影响，所带来的时间顺序上的“先”与“后”。须指出，这里所说的“先”与“后”，是指：用光速的绝对速度c来除以新物理点与原始物理点（它的运动起点）之间的空间距离r，所得出的滞后的时间过程?t =r/c，而不是用该物理点本身的移动速度υ去除以这个空间距离r所得出的时间过程t。

    正如所述，广义时空相对论认为：各种几何学在性质上的差异，是来自于几何公理的相对性。诸如：欧几里德几何，是在假设相互作用的传播速度为无穷大的前提下成立的；罗巴切夫斯基几何是在假定相互作用的传播速度大于真空中的光速而小于无穷大的前提下成立的。所以说，无论是欧几里德空间的平坦性，还是罗巴切夫斯基空间的弯曲性，都是来自于几何公理的相对性，而不是因为空间和时间本身具有几何性质。譬如说，如果我们把速度等于无穷大的“移动”作为一个“基准面”的话，那末，对于这个给定的“物理点”，考虑到它的移动速度的有限性（等于真空中的光速），比较而言，由这个物理点的移动所形成的空间位置肯定与速度等于无穷大的移动不在同一个基准面上。考虑到时空的均匀性，朝向任何方向的移动都是如此。移动后的位置与基准面之间的“最小高度差”就是光线在这一段移动距离上传播时所需要的滞后的时间过程。毫无疑义，如果相互作用的传播速度是无穷大，这两个点之间就不会存在着“高度差”。如果这个物理点在空间上的移动不存在，而只有时间的流逝，那么这个物理点就只在时间轴上变化。由此可见，罗巴切夫斯基几何（或黎曼几何）的“曲率”是来自于最大移动速度的有限性，而不是来自于引力场和物质分布的不均匀性。

    一言以蔽之，传统的数学抽象，并没有摆脱绝对同时性的时间观念。因此说，传统的“数学的抽象也只是在纯粹的数学中才是无条件地有效的”。

二    欧几里德几何公理

    为了阐明广义时空几何学原理，我们需要简单地重温一下欧几里德几何公理。这些公理大部分也是罗巴切夫斯基几何公理（参见[2]第126—127页）。它们的内容是：

1、结合公理

1），通过每两个点有一条直线，并且只有一条直线；2），在每条直线上至少有两个点；3），至少存在三个点不在一条直线上。

2、顺序公理

1），在直线上的三个点中，只有一个点在另外两个点之间；2），如果A、B是一条直线上的两个点，则在这条直线上至少有一个点C，使得点B在点A和点C之间；3），直线把平面分成两个“半平面”。
3、移动公理

1），移动把直线变成直线；2），一个接着一个地进行两个移动，相当于进行某一个移动；3），设A，A’和a，a’ 是两个点和分别从它们引出的半直线，β和β’ 是分别以延长后的直线a和a’ 为界的半平面；存在着唯一的移动，把A变成A’，a变成a’，β变成β’.（直观地说，用平移把点A变到A’，然后用旋转把半直线a变到a’，于是，半平面β或者与β’重合，或者还需要进行绕直线a的“翻转”。）

4、连续公理

设点X₁，X₂，X₃，……分布在一条直线上，使得每个在后的点都在其前一个点的右侧，但是同时有着处在所有这些点右侧的点A。那么就存在这样的点B，它也在所有的点X₁，X₂，……的右侧（都改成左侧是一样的），但是有着离它任意近的点X_n（即不论在点B的左侧取怎样的点C，在线段CB上总有点X_n）。

5、平行公理

通过已知点只能引一条直线不与已知直线相交。

三    罗巴切夫斯基几何公理

    罗巴切夫斯基几何是在欧几里德几何公理的基础上，仅修改了“平行公理”而创立的。罗巴切夫斯基把平行公理表述为：通过直线外的点至少能引两条直线不与已知直线相交。

四    广义时空几何原理

    广义时空几何学原理，是在同时放弃欧几里德几何和罗巴切夫斯基几何的“顺序公理”及“平行公理”的基础上而创立的。在广义时空几何中，直接引入了“客观性公理”——客体具有不依赖于主体的客观内容，——然后证明：欧几里德几何和罗巴切夫斯基几何的“平行公理”与“顺序公理”，只是广义时空几何在特定条件下的一些“推论”。

1、根本不存在严格意义的欧几里德空间（或惯性坐标系）

    考虑到光速是目前已知的宇宙中最快的信号传播速度，以及光速传播的有限性，所以根本无法实现“绝对同时性”。严格地来讲，只有当两个时钟重合于一点时，才有“绝对同时性”可言。由此而论，严格意义下的“惯性坐标系”只能把坐标原点选择在运动物体之上，除此之外的任何坐标系都不是严格意义的“惯性坐标系”。换句话说，除了运动事件本身以外，任何以其它事件为“参照物”的坐标系统都不是惯性坐标系。因此，客观上也根本不存在严格意义的“欧几里德空间”。普通力学所定义的惯性坐标系，是把观测者置身于运动事件之外，使用着统一的时钟，这只能是一个近似成立的物理概念。

2、广义时空概念

    基于上述观念，一个客观事件的时空位置，实际上就只能同时用四个坐标来共同地确定。这四个坐标为：三个空间坐标和一个时间坐标（时钟），它们之间是相互独立的。这种用“四度坐标”表示的“点”，叫做“世界点”。把所有的“世界点”人为地“集合”就构成了一种“空间”，我们把它叫做“广义时空”。在广义时空上，每个世界点都对应一个观测者和一个时钟。每个事件都有自己的“时空起点”，但却没有“公用的时钟”，因而也没有“统一的时空起点”。从这种意义上来看，我们所面临的广袤的宇宙，乃是一种“广义时空”，而不是“惯性时空”。所谓的惯性时空，仅仅是在一个较小范围上才近似地成立的相对性的概念。

3、广义时空上的线段

    我们把用四度坐标表示的两个世界点之间的“间隔”，叫做“广义线段”。对于“带撇”和“不带撇”的两个世界点（即坐标系K和K’）来说，它们到某一指定“起点”之间的“时空间隔”可以分别地写成：

x_i=(x₁² + x₂² + x₃² + x₄²)^1/2 ，x₄=ict .                         (1）

    以及，

x_i’=(x₁’² + x₂’² + x₃’² + x₄’²)^1/2，x₄’=ict’.                         (2）

    在欧几里德空间（惯性时空）上，带撇和不带撇的两个“物理点”之间的“距离”可写成：

    r =[(x₁-x₁’)²+(x₂-x₂’)²+(x₃-x₃’)²]^1/2；                             (3）

    推论一：表示同一个事件的广义线段对任何观测者来说都是相等的。

    这是“客观性公理”的第一个推论，物理上叫做客观性原理。注意到，当运动坐标系K’（即带撇世界点）上的观测者以自己所处的“位置”为参照物时，“主观感觉”自己是静止的，即：由上式所确定的移动距离r = 0. 由此得出：

            t’ = t(1 - V²/c²)^1/2.                                         (4）

其中，

            V² =(x₁² + x₂² + x₃²)/t²，                                     (5）

    是不带撇系（K）上的观测者得出的带撇系（K’）上观测者的运动速度。我把不带撇系（K）上的观测者叫做旁观者，而把带撇系（K’）上的观测者继续叫做观测者。并且把旁观者测算观测者的运动速度叫做相对速度，用“V”来表示；而把观测者计量自己对于旁观者的相对运动速度叫做绝对速度，用“υ”来表示。于是，由(4）式我们不难看出：

    1），当V →0时，意味着K’ 和K重合于一点，时间具有绝对同时性t’→t，这就构成了抽象的“欧几里德空间”，在欧几里德空间上成立的几何，就是欧几里德几何；

    2），当c →∞时，意味着信号的传播速度为无穷大，时间也具有绝对同时性t’→t。这就构成了抽象的“惯性时空”，其惯性时空上成立的力学定律，就是牛顿力学。

    不难理解，只有在以上这两种情况下，才有绝对同时性可言。然而，光速c是个有限的常数。所以不同时性就是绝对的，同时性只是一个相对的概念。由此可见，(4）式中的因子(1-V²/c²)^1/2便是两个“时钟”之间不同时性的“特征系数”，我们不妨把它叫做“相对性系数”。请注意，在推导(4）式的过程中，我们令r = 0，这就意味着运动坐标系上的观测者没有运动。可是，并非是观测者真的没有移动，而仅仅是由于参照物的选择导致了观测结果的相对性。这就如同坐在飞机里的观测者再以飞机为参照物的情况完全一样。如果若以飞机场为参照物，他的实际移动距不等于零（r ≠0）。其中，r乃是飞机的实际飞行距离，也是旁观者测量观测者的移动距离。这里，仅仅是由于观测问题的角度不同导致了“主体”对“客体”观测结果的相对性。

    为了体现出带撇和不带撇坐标系之间的区别，我们分别用r’ 和r来表示观测者和旁观者对同一个物理量“主观感觉”的不同（这仅仅是主观感觉，事实上总有r’≡r）。根据以上讨论，按照定义，绝对速度υ= r’/t’，而相对速度V = r/t。再由(4）式可以得出：

    υ= V/(1 - V²/c²)^1/2，                                         (6）

    或者改写成：

            V = cυ/(c² +υ²)^1/2.                                         (7）

    不难看出，当相对速度V →c时，就意味着绝对速度υ→∞.这个结论刚好说明：属于静止系的旁观者在利用绝对同时性的时间观念。因为，只有站在运动系上的观测者使用运动的时钟才能得出光速c，如果位于静止系的旁观者也能得出光速c，那就说明静止时钟和与运动时钟绝对地同步。事实上，这是绝对不可能的。所以说，光的相对速度并非是一个不变的物理量。

    推论二：同一事件的时间过程与观测者所处的位置无关。

    这是“客观性公理”的第二个推论，它的物理基础是“时空的均匀性原理”和“光的绝对速度不变”。证明也是非常简单的只要根据客观性公理认为所有的广义线段都相等，即：

            Δx_i¹ =Δx_i²=Δx_i³…Δx_iⁿ（i =1，2，3，4；n =1，2，3，…）。

    而n代表不同四度坐标系的编号。再由光的绝对速度不变，可以得出不同时钟所表示的时间间隔都相等，亦即：

Δt¹ =Δt²=Δt³ …Δtⁿ（n =1，2，3，…）。                     (8）

    可以把(7）式的两边分别地乘以用上式所表示的时间间隔Δt，从而得出：

r = r’c/(c² +υ2)^1/2.                                         (9）

让我们令：

            ξ= c/(c² +υ²)^1/2，                                         (10）

    显然，ξ表示着“旁观者”和“观测者”之间，由于所处的位置不同而表现出的“相对性特征”。我们把它叫做“相对性系数”。不难看出，在普遍的情况下（υ≠0），总有：

            0 <ξ< 1.                                                 (11）

    根据(10）式的结果，可将坐标系K和K’上的“空间”和“时间”变量分别地用不带撇的（x，y，z，t）和带撇的（x’，y’，z’，t’）来表示，那么，K和K’ 之间的变量便满足于：

    x =ξx’，y =ξy’，z =ξz’，t =t’/ξ，                         (12）

    上式充分地体现出：同一个客观事物对于不同的观测者来说“主观感觉的相对性”。

    这里要特别强调地指出：由于“时钟”是绝对不同时性的，所以，一个事件空间坐标的任何改变都对应着时钟的改变。因此，由x，y，z和t所确定的线段乃是一个四度线段，——即“广义线段”。千万不要把它与传统惯性时空上的“线段”混为一谈。因为它是由时间的绝对不同步导致了世界点的移动。所以说，除了以运动物体为参照物的坐标系以外，任何以其它物体为参照物的坐标系都不再是惯性坐标系！由此可见，洛伦兹变换决不是两个不同惯性坐标系之间的坐标变换，而仅仅是两个四度坐标系之间的坐标变换。这里，只有在极端的情况下（即主观地认为r’ = 0的情况下），才可以把洛伦兹变换当成是惯性坐标系与任何其它四度坐标系之间的坐标变换。

    一种特殊情况是：对于静止系的观测者来说，当V →c 时，ξ→0，则带撇系的空间尺度r’→0，时间过程t’→0. 其中，t’→0意味着带撇系的时钟慢地几乎停摆；而r’→0意味着空间尺度收缩为一个“点”。所以，不带撇系的观测者看来，带撇系上任何有限的空间尺度和时间过程都集中于“一点”，宇宙是“一”，过去、现在和未来是“全息的”。须指出，所以能得出这种结论，肯定是静止系的观测者在利用绝对同时性的时间观念。另一种特殊情况是：当υ→0（或υ<<c）时，ξ→1（或ξ≈1），“广义时空”就化成“欧几里德时空”。

    应该说，广义时空几何学的物理基础是广义时空相对论。或者说，广义时空几何是对广义时空观念的数学抽象。在某种意义上，广义时空几何和罗巴切夫斯基几何有许多相似之处，但也有所不同。其主要区别是：广义时空几何考虑了相互作用传播速度的有限性，也就是，考虑了相互作用传播速度影响的几何抽象；而罗巴切夫斯基几何是建立在相互作用传播速度是无穷大的基础上，或者说，不考虑相互作用传播速度有限性影响的几何抽象。

    的确，如果没有罗巴切夫斯基几何为先导，广义时空几何的一些结论是骇人听闻的。可是在罗巴切夫斯基几何理论成就的基础上，这些结论就不值得大惊小怪了。归根结底，我们可以说，罗巴切夫斯基几何和欧几里德几何之间的根本区别仅在于“平行公理”。而广义时空几何除了抛弃前两种几何的平行公理之外，同时还抛弃了它们的顺序公理，并且把平行公理和顺序公理作为它的推论，在证明中体现出来。这就是三种几何原理之间的根本区别。

五    广义时空几何的一般定理

    上述讨论已经证明：只有在运动坐标系K’上的观测者看来，时间才具有“绝对同时性”。所以说，只有“同观测者一起运动的坐标系”才是“惯性坐标系”，也只有在惯性坐标系上欧几里德几何才能成立。基于这一点，利用下图中的ΔABC“边”与“角”之间的相互关系，我们可以导出广义时空几何学的各种基本定理。

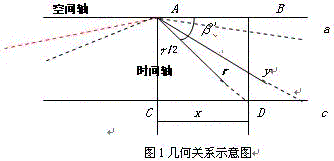
    在图1中，所设：直线a是事件以无穷大速度移动时所形成的基准线，而直线c是以光速移动时而引起的偏离基准线的极限位置。图中的半直线r具有广义时空几何意义、且不与直线c相交，或者说，二者相交于无穷远点。

    为节省篇幅，这里只介绍八个定理。有兴趣者，可参考上述的做法，自己来加以推广。

1、勾股弦定理

    我们用带撇的符号表示欧几里德空间上的变量，而用不带撇的符号表示广义时空上的变量，在上图中，可以得出：

r’² = x’² + y’² = (x² + y²)/ξ²，                             (13）

或者写成：

            x²+y² =ξ² (x’² + y’²)。                             (14）

    而ξ²可以写成：

            ξ² = 1/(1 + υ²/c²)。                                 (15）

    为了方便两种不同类型几何学之间的比较，我们把ξ²按幂级数展开，则有：

            ξ² =1-(υ²/c²)+(υ²/c²)² –(υ²/c²)³ + …，                     (16）

    将(27）式代入(25）式，可以得出《广义时空几何》的“勾股弦定理”：

    x² + y² =(x’² + y’²)[1-(υ²/c²)+(υ²/c²)² –(υ²/c²)³ + …]。    (17）

    显然，在υ<< c时，上式化为：x² + y² ≈ x’² + y’²，这就是说，在绝对速度（υ）较低时，广义时空几何的勾股弦定理过度成欧几里德几何的勾股弦定理。或者说，广义空间过度成欧几里德空间。但是，在(υ/c) > 1时，由于上面的级数不成立，所以，在广义时空上，勾股弦定理并不能严格地成立。相同的道理，我们可以写出以下的定理。

2、正弦定理

    由(1）式得出：

sinβ’=y’/(x’²+y’²)^1/2=ξy’/(x²+y²)^1/2.                      (18）

由此可以写出：

sinβ= y/(x²+y²)^1/2 .                                     (19）

3、余弦定理

由(1）式得出：

cosβ’=x’/(x’²+y’²)^1/2 =ξx’/(x² + y²)^1/2，                     (20）

由此可以得出：

cosβ= x/(x² + y²)^1/2.                                     (21）

4、正切定理

由(18）和(19）式得出：

                tngβ’= y’/x’≡ y/x = tngβ.                             (22）

5、余切定理

由(22）式可以得出：

ctgβ’= x’/y’≡ x/y = ctgβ.                             (23）

6、不存在面积任意大的三角形

在欧几里德几何中，一个矩形和一个三角形的面积可以分别地写成：

S_□’ = a’h’，及 S_Δ’ = (1/2)a’h’.                         (24）

其中，a’和h’是矩形的长和宽。如果我们以相同的方法定义广义矩形和广义三角形面积的话，则有：

S_□ = ah ，及 S_Δ =(1/2)ah.                             (25）

    由(26）式得出：

                S_Δ = (1/2)ξ² a’h’.                                      (26）

    将ξ²展成幂级数代入上式，则得到广义三角形的面积为：

S_Δ=(1/2)a’h’[1-(υ²/c²)+(υ²/c²)² –(υ²/c²)³ + …]，                 (27）

    当υ²/c² < 1时，上面的级数成立，我们可以得出广义三角形的面积S_Δ. 但是，如果不考虑υ的实际取值范围，例如，假设当υ²/c² >1时，上面的级数就不成立，我们将无法得出广义三角形的面积。所以说，不可能有面积为任意大的广义三角形。

7、圆周长度不与半径R成正比

    在欧几里德几何中，圆的周长可以写成：

ι= 2πR，                                             (28）

    用R =ξR’代入上式，可以把广义时空上圆的周长写成：

                ι= 2πξR’.                                             (29）

    把ξ按幂级数展开得：

        ξ= 1-(υ²/c²)/2 + 3 (υ²/c²)²/8 –15(υ²/c²)³/48 + …，             (30）

    由此得出：

ι= 2πR’-(πR’υ²/c²)+ 3πR’(υ²/c²)²/4-5πR’(υ²/c²)³/8 + …，     (31）

    当υ²/c² < 1时，上面的级数成立，可以得出广义时空上圆周的长度。但是，如果不考虑υ的实际取值范围，例如，假设当υ²/c² >1时，上面的级数并不成立，因此无法得出这种圆的周长。惟有υ<< c时，圆的周长才等于2πR’，普遍的情况并不等于2πR’.

8、半径无限增加的圆周的极限不是直线

    由(31）式看出：对于υ= 0→∞，圆周的长度是一条曲线而不是一条直线。所以说，半径无限增加的圆周极限也不是直线。如此等等，我们不再列举。总而言之，这些性质与罗巴切夫斯基几何的性质基本上是一致的。

六    广义时空几何与欧几里德几何的关系

    按照欧几里德几何的平行公理，两条平行线的夹角β’=0时，应有cosβ’=1。由(20）式看出：当β’= 0时，应有：

    ξx’ =(x²+y²)^1/2.                                         (32）

    可是，根据定义，ξx’= x，所以上式只有在y = 0时才能成立。在图1中，y = 0就意味着线段a和线段r之间没有“交点”，即：这两条“半直线”不相交。所以，欧几里德几何的平行公理可以叙述为：“通过已知点只能引一条直线不与已知直线相交。”可见，欧几里德几何的平行公理是广义时空几何的推论。

    除此之外，由于广义时空上的线段并不是“直线”，而是一条“曲线”。所以，它不可能把一个“真平面”分成两个部分。因此，在广义时空上顺序公理并不成立。道理是很简单的，因为由一条曲线平移所构成的面是一种“曲面”。一条直线不可能把一个曲面分成左、右两个部分。只有当ξ= 1时，广义时空化为欧几里德时空，曲面伸展为真平面，顺序公理才能够严格地成立。

七     广义时空几何与罗巴切夫斯基几何的联系与区别

    由(32）式可以看出，一般的情况，总有：

x’ <(x² + y²)^1/2/ξ，                                     (33）

极限的情况是，β’→0，则有：

x’→(x² + y²)^1/2/ξ.                                      (34）

    显然，上式只有在y →0时成立。而y →0意味着两条直线不相交。但在逻辑上，无穷远处不相交的线段可以有无数条，因为，凡是能够指出位置的交点都不是无穷远，所以罗巴切夫斯基几何的平行公理可以叙述为：通过直线外的点至少能引两条直线不与已知直线相交。

八    三种几何学的相互比较

    诚如上述，利用广义时空相对论的时空观念，我们还初步地创立了一门新的几何学原理，我把这种几何学叫做广义时空几何原理。现将欧几里德几何、罗巴切夫斯基几何（或黎曼几何）、广义时空几何的基本要点比较如下：

欧几里德几何	罗巴切夫斯基几何	广义时空几何
时空的几何性质是平坦的。	时空的几何性质是弯曲的。	时空根本没有几何性质。
牛顿力学在其中成立。	爱因斯坦相对论在其中成立.	广义时空相对论在其中成立.
时间和空间是绝对不变的，因而度规是刚性的。	时间和空间的可变性是真实的，因而度规是可变的。	时间和空间的可变性是相对的，度规是刚性的。
站在运动事件之上、用运动时钟，对处于静止状态的物体抽象出来的时空。在这种时空中有：υ= 0. 以及，相对性系数：ξ= 1.	站在运动事件之外、用静止时钟对介于光速和无穷大的绝对速度之间状态的物体抽象出来的时空。这种时空中有：c <υ<∞，以及相对性系数：O < ξ< /2.	站在运动事件之外、用静止时钟对介于光速和无穷大绝对速度之间状态的物体抽象出来的时空，这种时空中有：0<υ≤c，以及相对性系数： /2 ≤ξ< 1.
有物质基础。	没有物质基础。	有物质基础。

可以说，通过广义时空相对论的时空观念，我们不仅可以清楚地阐明广义时空几何学、欧几里德几何学、以及罗巴切夫斯基几何学（或者黎曼几何学）之间的相互关系，而且还可以指出各种几何学成立的“物质基础”。除此之外，从“绝对瞬时性”的时间观念出发，我们又建立了一种全新的相对论，并把它叫做“狭义时空相对论”这种全新的时空理论可以为《仿射几何学》的研究提供一种新的讨论方法。

九    结    论

总而言之，这一全新的几何理论为广义时空相对论提供了有力的数学依据。或者更确切地说：广义时空相对论为广义时空几何提供了可靠的物理基础。从广义时空相对论的物理实践证明，这一几何原理不仅可以解决现代物理学中各种已知的时空问题，而且可以用于解决现有理论一直无法解决的时空问题。特别是这里所证明的关于“存在着一种没有因果规律的时空”的结论，的确是骇人听闻的！但这确实是逻辑推理的必然结果。当然了，这个结论必须建立在：所有以光速运动的物质将构成一个“统一的、连续的、不可分割的整体”的前提下。相信这一结论对现代物理学和哲学的研究与发展，甚至对于人体科学的研究与发展，都将产生极为重要的影响。  

  不仅如此，通过以上的讨论，还可以清楚地证明，爱因斯坦的狭义相对论和他的广义相对论都不是唯一正确的时空理论。所以，我们绝对不应该根据爱因斯坦相对论所取得地巨大成就，来掩盖理论本身的逻辑谬误和概念错误。事实证明，以恩格斯的自然辩证法为基础所建立的广义时空相对论，是一个比爱因斯坦的狭义相对论和广义相对论都更加正确的时空理论。它不仅可以解决爱因斯坦的相对论已经解决的时空问题，而且可以解决爱因斯坦的相对论一直无法解决的时空问题。毫无疑义，广义时空相对论的创立，为现代物理学、现代数学、现代宇宙学、以及现代自然哲学的研究工作，提供了一个前所未有的理论基础。

参考文献

[1]《广义时空相对论》夏烆光著，北京，人民交通出版社，2003年1月第一版，第七章，第八章。

[2]《空间·时间·和引力的论》B·A· 福克著，周培源，朱家珍，蔡树棠等译，北京，科
学出版社，1965年7月第一版，第288页。

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页