物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-时空的绝对与相对
《二十世纪物理学批判》第一篇
论文四
时空的绝对与相对
吴 家 荣
内容提要：根据光速不变原理，建立绝对时空和相对时空的概念，为推导洛仑兹变换新公式奠定了基础。
关键词： 时空概念 绝对与相对
一、光速恒定原理是我们认识世界的基础
爱因斯坦光速恒定原理我们重述于下
在“静止”坐标系统中，光线无论从静止物体还是从运动物体上发射出来，都以确定的速度ｃ运动。
这条原理是我们认识自然界的基础，由光速恒定原理，我们将推导出洛仑兹变换，而“相对性原理”则是光速恒定原理的自然推论。通常认为相对论具有两条基本原理，这是不正确的。关于这个问题我国著名数学家华罗庚教授早就指出：
“1946年作者研究矩阵几何学时，用了一个方法，这方法可以用来处理ｎ维球空间的基本定理，也就是用球相切性可以推出球几何学的基本定理，也就是不必用变换的解析性，甚至连续性，就可以推导出其变换群是球几何学的Ｌie群，Ｌoguerre群。
这儿只讲三维空间的球几何学，其原因是一方面比较具体，易于接受，另一方面企图使这一成果能为一些物理工作者注意。实质上三维的球几何学就是狭义相对论的另一表达方式，而这点往往未被认识。例如1961年，Ｂ·Ａ·ΦΟＫ写的《Теория просем рансмва，временаи теромения》一书（有中译本，1965年，科学出版社），书中仍旧用的是Ｒｉｅｍａｈｎ几何、解析群论的老路子，而中、英、德等文的译本中也都未注意到这一点，而加以应有的注记。
对狭义相对论来说，原有两个假设：
（Ａ）、相对性原理中要求匀速直线运动还是匀速直线运动。
（Ｂ）、光速不变原理是假设光以常速ｃ作直线运动。
我们现在的处理方法是有了光速不变原理，就可以推出Ｌｏｒｅｎｔｚ群了，就是相对性原理中要求匀速直线运动还是匀速直线运动是推论而不是假设。这给我们提供了方便，如果要验证或推翻上述两点，只要用实验来检验光速不变性就够了”[1]
遗憾的是华罗庚教授的这一重要成果，并未引起我国物理工作者所注意，对华教授这一指示的重要性“往往未被认识”，而华教授的这一指示早在1962年就已作出。
所谓光速恒定就是光具有定速，不管它的速度值多大，都不影响洛仑兹变换的推导. 或者说洛仑兹变换公式的推导，只与光速的概念有关，而与光速值的大小无关。
观察时间的相对性与物体的空间位置，物体的运动速度以及物体运动相对于光传播的方向有关。
二、空间、时间的概念
同时性、同步性、时间差的定义
（一）、绝对同时、同步性
如果在空间的Ａ点有一个钟，在Ａ点的观察者只要在事件发生的同时记下指针的位置，就能确定Ａ点最邻近处的事件的时间值。若在空间的另一点Ｂ也有一个钟，此钟在一切方面都与Ａ钟类似，那么在Ｂ点的观察者就能测定Ｂ点最邻近处的事件的时间值。但是若无其他假设，就不能把Ｂ处的事件同Ａ处的事件之间的时间关系进行比较。
到此为止，我们只定义了“Ａ时间”和“Ｂ时间”，还没有定义Ａ和Ｂ的公共“时间”。除非我们用定义规定，光从Ａ走到Ｂ所需的“时间”，否则公共“时间”就完全不能确定。现令一束光线于“Ａ时间”
从Ａ发射向Ｂ，于“Ｂ时间”
又从Ｂ被反射向Ａ，于“Ａ时间”t′A 再回到Ａ。
我们假定，同步性的这个定义是无矛盾的，能适用于任何数目的点，并且下列关系总是成立的：
1、假如Ｂ处的钟与Ａ处的钟同步，则Ａ处的钟与Ｂ处的钟也同步。
2、假如Ａ处的钟与Ｂ及Ｃ处的钟同步，则Ｂ、Ｃ两处的钟彼此也同步。
这样借助于某些假想的物理实验，我们解决了如何理解位于不同地点的同步静止钟这个问题，并且显然得到了“同时”或“同步”的定义，以及“时间”的定义。事件的“时间”就是位于事件所在处的静止钟在事件发生的同时给出的时间，这个静止钟是校准过的，它在一切时间测量上都与一个特定的静止钟同步。
根据经验，我们进一步假定，量
(1)
是个普适恒量，即在真空中的光速。
重要的是，我们要用静止在静系统中的时计来规定时间矛而现在所定插的时间既然适合于静系统，我们就称之为“静止系统的时间”。
以上，是爱因斯坦关于“时间”、“同时”或“同步”的定义[2] 。以后我们会明白，爱因斯坦这里定义的实际上是牛顿的“绝对时间”。我们把这种“爱因斯坦同时性”称为绝对同时（或同步)。爱因斯坦仅仅作了这一定义。然而，关于时间还应有以下几条定义。
（二）、相对同时性
设空间Ａ点、Ｂ点和Ｏ点各有一只爱因斯坦钟，这三个钟是绝对同时同步的。在Ｏ点的邻近处有一个观察者观察Ａ钟和Ｂ钟。在某时刻，从Ａ钟发射出的光信息到达Ｏ点处观察者眼中时，观察者看到Ａ钟指示着时间
；在同一时刻从Ｂ钟发出的光信息，也到达Ｏ点处观察者眼中时，观察者看到Ｂ钟指示着时间t
?B 。如果
我们定义Ａ钟与Ｂ钟同时．但光有定速，光传播需要时间，观察者看到它们与自己身边的Ｏ钟是不同时的。即
我们把Ａ钟与Ｂ钟的这种同时性称为相对同时。
（三）、时间差
１、本钟时间差
如果Ａ钟在某时刻指示
，在另一时刻指示
，那么我们把
称为Ａ钟的时间差。同样，我们可以定义Ｂ钟的时间差，Ｃ钟的时间差，Ｋ钟的时间差等等。统称为本钟时间差。
２、两钟时间差
设空间Ａ点与Ｂ点各有一只爱因斯坦钟，在某时刻，由观察者看来，如果Ａ钟指示
与Ｂ钟指示时间
在数值上不相等，且tB
＞ tA ，我们把（ tB － tA）定义为Ｂ钟与Ａ钟的两钟时间差。
３、静系时间差、动系时间差、时间差之比
| 让我们在“静止”空间取一个静坐标系Σ和一个动坐标系Σ′，使两系统Ｘ轴重合而Ｙ轴和Ｚ轴平行。令动系统Σ′的原点沿着静系统Σ的Ｘ轴增加方向以 速度ｖ作匀速平移运动。在静系Σ原点和动系Σ′原点各放置一个钟，它们相对于各自的系统都是静止的。为了和以后的讨论统一，我们把静系原点处钟叫Ｋ钟，把动系点处钟叫Ａ钟。如图１所示。 |
 |
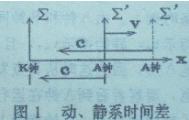现在我们设想，在静系统原点处有一观察者来看这两个钟。某时刻动系Ａ钟发来的光信息到达观察者，此时刻观察者看到Ｋ钟指示
在另一时刻，反映动钟信息的另一束光线到达，观察者看到静钟指示
我们定义
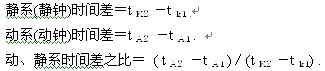
（四）、相对同步性
如果静系（静钟）时间差和动系（动钟）时间差在任何时刻都相等，我们就认为静系统中的Ｋ钟和动系统中的Ａ钟是同步的。按照定义，两钟相对同步的条件是
相对同步的两钟，可以不同时。这和爱因斯坦定义的绝对同步性是有区别的。好比两个人的表，运行绝对准确，但两个人的表“对时”有误差。
三、空间（长度）的绝对性和相对性
（一）、长度的绝对性
设有一根“静柱”的刚杆AB，我们怎样来测量这杆的长度呢? 一种办法是用静止的标准量杆一杆一杆地去测量，但这种测量不够准确。既然我们把光速恒定原理作为我们认识世界的基础，我们还是借助于光来测量。测量的方法是在杆AB的Ａ端设置一个精确的钟。从杆Ａ端向Ｂ端发射一束光，当光到达Ｂ端时，使光反射回Ａ端，测出发射与接收的本钟时间差，我们就能计算出这个杆的长度。这个方法其实就是爱因斯坦同时性定义方法。由公式（１）我们得到
根据光速恒定原理，光在静止系统和在运动系统传播速度都是C。所以不论这个杆是处于“静止”状态，还是运动状态，用光测出的长度都是一样的。这就是空间距离的绝对性。
所谓“静止”状态和运动状态也是相对的。如果我们在运动状态中进行测量，我们以为自己是“静止”的，这种测量和在“静止”状态中的测量没有两样；否则“相对性原理”就要失效。
如果将“光在静止系统和运动系统传播的速度都是ｃ”理解为不受运动系统影响的ｃ。这一方面将导致承认绝对静止的存在：即光传播速度为ｃ的那个参照系才是“静止”系统。另一方面也不能否定绝对长度的存在。因为由
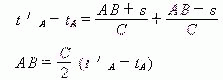
测到的仍是杆的绝对长度。
（二）、长度的相对性
设在“静止”空间取一“静止”坐标系Σ
，原点处有不静钟Ｋ。有一根刚杆AB平放在Ｘ轴上，Ａ点与坐标Σ原点重合。用上述方法测量，我们得到一个“静止”杆长。令杆AB以速度ｖ沿Ｘ轴增加方向作匀速平移运动，在这杆的Ａ端和B端各有一个随杆一同运动的Ａ钟和Ｂ钟。这三个钟是按绝对同时性定义校准过的。在静系原点处有个观察者同时观察这三个钟。设想某时刻
t O
由Ａ钟和Ｂ钟同时发出两束光信息，当Ａ钟的光传到观察者时，观察者看到Ａ钟指示
。此时观察者并不知道杆有多长，他看到的只是Ａ点，因为这时从Ｂ点发出的光信息还没有到达。杆以速度ｖ向前运动，不断地发出光信息，观察者看到Ａ钟在运行。当Ｂ点光信息到达时，观察者同时看到了三个钟的信息。此时Ｋ钟指示
如图２所示。
由于（tA′－ tA ）是观察者看到的反映了杆的运动状态的时间差，动杆的相对长度要以这个时间差来计算：
观察者看到的这个运动杆的长度一定是小于“静止”杆的长度。我们把杆在运动状态下，由静止系统测量的这个长度，定义为杆的相对长度。（相互考察）
反映了Ｂ点发出的光走到Ａ点的时间差，即Ｂ点发出的光走完杆的绝对长度所需要的时间。
而（tA′－ tA ）反映了Ｂ点发出的光走到Ａ′点的时间差，即Ｂ点发出的光走完杆的相对长度所需要的时间。
四、观察时间的相对性
我们的宇宙，不可能有超出我们认识的东西。而要认识它，就要感觉它。我们依靠眼、耳、口、鼻、身五官获得五种感觉，即视觉、听觉、味觉、嗅觉和触觉，其中最基本的是视觉。而谈视觉离不开光。光，既是使物体“显形”的物理原因，也是传递物体存在信息的媒介。
光信息的传递要通过空间距离，而光有定速，我们获得信息就需要时间。另外，我们自己是处于什么状态呢？“静止”还是运动？我们这个世界就是个运动的世界。因而，我们通过视觉认识世界，就是要搞清楚光速、时空和我们自己运动状态之间的关系，寻求它们的规律。
（一）、时间的相对性与空间点的位置有关
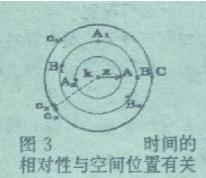
假如在“静止”空间中，各点都有爱因斯坦静止钟，它们都是经过同时性定义校准过的，因而空间各点的钟，都绝对的“同时同步”。在空间任意一点Ｋ钟的旁边有一观察者来观察空间各点处的静止钟。图３中，ｘ为空间Ａ点处钟到观察者处Ｋ钟的距离。设想某时刻
t O ，Ａ钟向观察者Ｋ钟发来一束光信息，因为Ａ钟与Ｋ钟是绝对同时同步的，当发出光信息的时刻，两钟指示的时间应该一样。但光有定速ｃ，通过ｘ距离到达观察者时观察者看到Ａ钟指示
根据时间差定义，我们得到
Ｋ钟与Ａ钟两钟时间差＝
光通过空间ｘ距离，用时是ｘ／ｃ，于是
|
或者
|
 |
两式相减
由公式（２）我们知道，Ａ钟比Ｋ钟“慢”了ｘ/ｃ 秒。 空间距离ｘ越大（如图３中Ｂ钟、Ｃ钟等），看起来钟越慢。但这种慢属于总是慢ｘ/ｃ秒，而不是每秒慢ｘ/ｃ秒。所以空间不同距离上的钟 ，看起来是“同步不同时”的。
空间相同距离ｘ各点处的钟，只要在观察者视野内（如图３中C2 、C3 非常邻近），能同时观察到，那么应该是“同时同步”的，但都比观察者处的钟慢了ｘ/ｃ秒。
观察者视野外，相同距离ｘ处的钟，观察者看不到。要看就得转身，这就改变了观察者的运动状态（相当于坐标转动变换）。这种改变是需要时间的，所以观察者不可能看到相同距离ｘ处的钟都相互“同时同步”地运行。当观察者重新选择自己的观察位置时，他将看到原来“同时同步”的钟不再“同时同步”；而原来“同时不同步”的钟有些又“同时同步”了。总之，时间的相对性与空间的位置有关。
结论：时间和空间的观察是不可分割的。在“静止”系统中，空间距离越远，看起来钟走得越慢。在观察者视野之内的空间球面上所发生的事件，在观察者看来是同时的。可以想到，既使是变速状态，只要运动物体不离开空间相同距离的球面，在观察者看来，它们也是同时的。
（二）、时间的相对性与运动速度的大小和方向有关
| １、相离运动 设空间有一“静止”系统Σ，在静系统原点处放一只 动钟Ａ在图示Ａ位置向观察者发出光信息，于 tA
到 |
 |
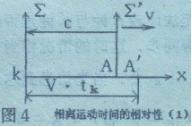位置。总共运动路程为ｖ· tK 。由距离、速度、时间相互关系我们推导如下：
时间内，光通过的路程为
而坐标移动的距离为
所以
（4）
或 
于是我们得出结论：相离运动的两钟，“既不同时也不同步”，运动钟走得慢，速度ｖ越大，走得越慢。相离而去的动钟每秒慢 v／(c＋v) 秒，变慢的比率为ｃ／(ｃ＋ｖ) 。
| 上述结论是观察者站在静系Σ立埸看到的情况。观察者若站在动系Σ′立埸看静系统，会看到什么情况呢？ 如图５所示，观察者站在动系立埸上，他以为自己是静止的，他看到静系Ｋ钟以速度ｖ向Ｘ轴减小的方向运动。由于实际上是动系Σ′以速度ｖ向Ｘ轴增加方向运动，观察者看到光源（Ｋ钟）发出的光信息到达的时间变慢。 |
 |
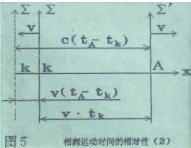因为
所以
（5）
或 
| 结论：相离运动时，若站在动系看静系，观察者看到两钟“既不同时也不同步”，静系Ｋ钟走得慢，速度ｖ越大，走得越慢，相离而去的静钟每秒慢ｘ／ｃ秒，变慢的比率为(ｃ－ｖ)／ｃ
。 ２、相向运动 |
 |
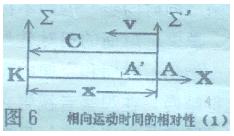到什么情况呢？
| 我们设想某时刻 t0
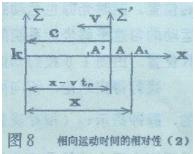
＝０，从与Ｋ钟相距ｘ距离处的Ａ钟发出光信息。由于信号传送到观察者需 要ｘ／ｃ时间，又由于Ａ钟运动的速度ｖ小于光速ｃ，所以在信号到达观察者之前，即 t k ＜ｘ/ｃ时，观察者对于Ａ钟的情况一无所知，既无法比较Ａ钟与Ｋ钟是否同时，也无法比较Ａ钟与Ｋ钟是否同步。这时的情况相当于公式（２）：给出的情况：tA = t k －ｘ/ｃ 。当光信息到达观察者时，观察者看到  。此时t K＝ｘ/ｃ
秒，tA ＝０。观察者看到动钟Ａ比静钟Ｋ慢了ｘ/ｃ秒，它们已经“不同时”
。现在我们考虑这两钟还同不同步。在光信息没有到达观察者之前，动钟Ａ一面以速度ｖ向静钟Ｋ作匀速平移，一面不断地发出光信息。当第一束光到达观察者后，观察者看到动钟Ａ由 t0 ＝０开始运行。此时动钟Ａ已运动到图7所示Ａ′位置。动钟Ａ的指针位置应与它所到之处的静钟指针位置相同，即动钟Ａ实际指示时间与静钟Ｋ一样，它们的绝对时间是相同的 。动钟Ａ已经运动到 Ａ′，而观察者看到的是它在距离ｘ处发出的信息。 当动钟Ａ运动到观察者身边时，观察者看到两钟指示一致。Ｋ钟指示tk′ ，Ａ钟也指示ｔk′（ｔA′＝ｔ＇k）。但观察者看到静钟Ｋ是由ｔk ＝ｘ/ｃ走到ｔk′的 ；而动钟Ａ却是由ｔA ＝０走到ｔk′。两钟已“不同步”。 于是我们得出结论：相向运动的两钟当观察者同时看到两钟信息后，两钟“既不同时也不同步”。距离ｘ越大，两钟越不同时；速度ｖ越大，两钟越不同步。相向而来的动钟走得快，如图７所示。 上面是定性的分析，现在我们来定量地推导相向运动时，动钟Ａ与静钟Ｋ之间的关系公式。 |
 |
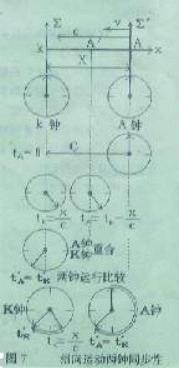＜１＞、首先我们研究由静系统Σ看动系统Σ′情况怎样 令与动钟Ａ固联在一起的坐标Σ′向着Σ系统Ｘ轴减小方 若计时开始时，两钟相距ｘ，当动钟运动到Ａ，动钟指示 根据式(2)有 |
 |
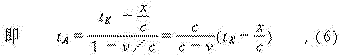
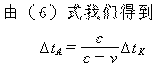
于是我们得出结论：相向而来的钟，站在静系统Σ立埸观察，静钟指示ｔK
， 动钟指示
动钟走得快,动钟每秒快 ｖ／(ｃ－ｖ)秒, 变快的比率为 ｃ／(ｃ－ｖ)
。但从钟面指针位置看，在动钟没有到达观察者之前，动钟Ａ总是比静钟Ｋ落后
(ｘ－ｖｔA)／ｃ秒 。
＜２＞、其次我们研究由动系统Σ′看静系统Σ情况怎样
站在动系统立埸，观察者相对于动系Σ′静止，他看到静系Σ原点处Ｋ钟以速度ｖ向自己运动，如图９所示。
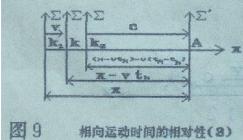
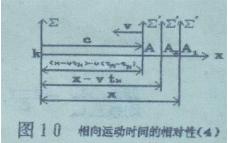
现在请先看图１０。若计时开始时，两钟相距ｘ，当Ａ钟由Ａ1 运动到Ａ2 ，Ｋ钟指示ｔk ，此时两钟相距(ｘ－ｖｔｋ)，与此同时，由Ｋ钟向动系Σ′原点Ａ2 发出一道光，传送静钟Ｋ的时间信息ｔk 。当ｔk 信息到达动系Σ′原点时，动钟Ａ已由Ａ2 运动到Ａ位置，观察者看到静钟指示ｔk ，动钟指示ｔA ， 此时两钟相距(ｘ－ｖｔk )－ｖ(ｔA－ｔk ) 。根据(2)式有
即
（7）
或
上述图１０是根据绝对运动观点画出的，目的是为了推导公式直观一些，也可以根据相对运动观点画出，如图９所示，结果是一样的。
值得注意的是Ｋ钟由Ｋ位置发出的光信息tK ，当观察者接收到tK 时，Ｋ钟已由Ｋ运动到k 2 位置，同时光源也运动到k 2 。这是和由静系看动系情况不同的。正是这一点，将两个相向运动的匀速平移坐标系统的不等价性表示出来。所以图９中的发光点是画在k 2 ，而没有画在Ｋ位置。由图１０我们知道其物理意义。
我们得出结论：相向而来的钟，站在动系Σ′立场观察，它们也是“既不同时也不同步”的。静钟指示t A（相对观察者来说Ａ钟静止），动钟指示tk ＝(c＋v)／ｃ· t A－ｘ／ｃ。动钟Ｋ（由动系观察者看来钟Ｋ是运动的）每秒快ｖ／ｃ 秒。变快的比率为(c＋v)／ｃ。但从钟面指针位置看，在“动钟”没有到达观察者之前，“动钟”Ｋ总是比“静钟”Ａ落后
（三）、时间的相对性取决于运动速度ｖ和光速ｃ的相对方向
关于时间的相对性取决于运动速度ｖ和光速ｃ的相对方向，前面的讨论已经涉及到，现在我们归纳一下：
１、相离运动
(１)、站在静系Σ立场观察动钟Ａ，光速ｃ与运动速度ｖ方向相反。图１１
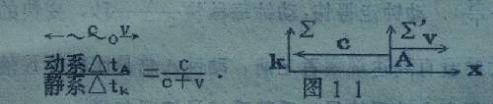
(２)、站在动系Σ′立埸观察静钟Ｋ，光速ｃ与运动速度ｖ方向相反。如图１２
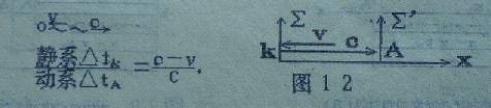
２、相向运动
(１)、站在静系Σ立埸观察动钟Ａ，光速ｃ与运动速度ｖ方向相同。如图１３
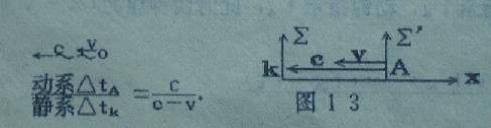
(２)、站在动系Σ′立埸观察静钟Ｋ，光速ｃ与运动速度ｖ方向相同。如图１４
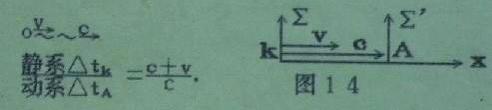
３、随动系Σ′一同运动，观察动系Σ′的Ａ钟与Ｂ钟
这种情况，观察者认为自己是“静止”的，他看到的Ａ钟与Ｂ钟指示和在静系统中看到相对静止的两个钟指示完全相同。
(１)、由Ａ看Ｂ，光速ｃ与运动速度ｖ方向相反。图１５
(２)、由Ｂ看Ａ,光速ｃ与运动速度ｖ方向相同。图１６
上述公式中的(ｃ＋ｖ)和(ｃ－ｖ)并不是光波的合成。光速恒定原理要求光波无论是在动系统还是在静系统都是以波速ｃ传播。公式中的(ｃ＋ｖ)和(ｃ－ｖ)是根据光子运动速度概念推导出来的。
另外，公式中符号ｖ→ｏ～→ｃ
表示光速ｃ与速度ｖ的相对方向，圆圈表示光源位置。
引文：
[1]、华罗庚，《从单位圆谈起》，第103 页，科学出版社，1977年。
[2]、爱因斯坦，“论动体的电动力学”，《相对论原理》，第34页，科学出版社，1980年。
现在我把已经导出和将要导出的关于“相对论新说”的几个重要公式列表于下
表4－1 相对论新说的重要公式
| 公式名称 | 方向 | 从静系Σ看动系Σ′ | 从动系Σ′看静系Σ |
| 相对时间和绝对时间的关系 | 相离 |  |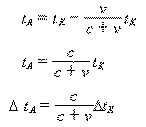
 |
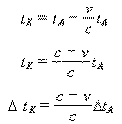| 相向 |  |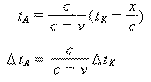
 |
|
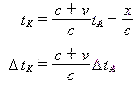| 时间差比值 | 相离 |  |
 |
| 相向 |  |
 |
|
| 推导洛仑兹变换的基本公式 | 相离 |  |
 |
| 相向 |  |
 |
|
| 洛仑兹变新换公式 | 相离运动 |  |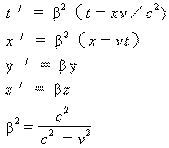
 |
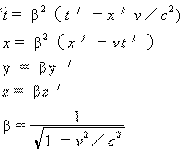| 相向运动 |  |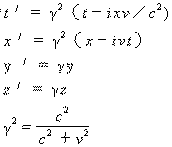
 |
|
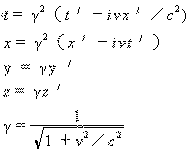| 能量公式 | 相离 | 
 |
|
| 相向 | 
 |
||
| v＜＜c | 
 |
||
| v＝0 | 
 |
||
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑
,而动钟Ａ已运动到Ａ′