物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-洛仑兹变换正确公式的初等推导
《二十世纪物理学》批判第一篇
论文五
洛仑兹变换正确公式的初等推导
吴 家 荣
内容提要:根据光速不变原理，两类镜像对称和时空的绝对与相对概念，运用初等数学的方法直接导出洛仑兹变换新公式。
关键词 洛仑兹变换 正确形式
经典洛仑兹变换是洛仑兹通过假设提出的，没有进行数学推导，而爱因斯坦在《论运动物体的电动力学》一文中的推导又有迎合经典洛仑兹变换的明显错误。如果爱因斯坦实事求是地将ｘ′＝ｘ－ｖｔ代入他自己导出的几个预备公式，就应该得出
其中：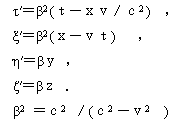
洛仑兹变换新公式的高等数学推导，如果爱因斯坦不随意处置一个系数β发生错误的话，实际上他是能够给出的。因为那是一个简单的代入计算，初中学生都会。
当然，他给出的也仅仅是含有β2 系数的一组公式，而给不出含有γ2 系数的共轭洛仑兹变换。创建共轭洛仑兹变换的概念，应是笔者的功劳。
现在我们来进行洛仑兹变换新公式的初等推导，这更能让多数人接受，因而更具说服力。
一、相离运动洛仑兹变换的推导
根据相离运动时钟变慢的观点我们来推导洛仑兹变换新公式。
（一）、从静系看动系
１、Ｘ轴坐标从静系统到匀速平移系统的变换
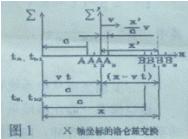
在空间取一静止坐标系统Σ，在Σ的Ｘ轴上平放一根刚性杆AB，令AB以速度ｖ向Ｘ轴增加方向运动。设
| 想在静系原点有静钟Ｋ，在杆AB的两端固定有钟Ａ和钟Ｂ。这些钟事先都校准过，是“同时同步”的。动系Σ′原点为杆Ａ点，杆AB相对于Σ′是静止的。如图１所示。 当Ａ钟从Ａ位置发出光到达观察者时，观察者看到静钟指示ｔk1 ，Ａ钟指示ｔA 而Ａ钟实际上已运动到Ａ1 位置.但因Ｂ钟在Ｂ位置发出的光信息还没有到达，观察者不知道杆有多长。当Ａ钟运动到Ａ3 位置时，它从Ａ2 位置发出的光和Ｂ钟在Ｂ位置发出的光同时到达。这时观察者看到静钟指示ｔk2 ，动钟Ａ指示ｔA2 ，而动钟Ｂ指示ｔB ＝ｔA2 ，根据论文四《时空的绝对与相对》相离运动公式(４)我们得到 |
 |
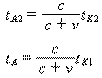
即
其中： （ｔA2 －ｔA ）为静系观察者看到的反映杆的相对长度的动钟两钟时间差或相对时间差。
（ｔK2 －ｔK1 ）为静系观察者看到的反映杆的绝对长度的静钟本钟时间差或绝对时间差。
由图１，可见动钟Ａ在Ａ2 位置发出的光是与动钟Ｂ发出的光同时到达观察者。光通过 (ｘ－ｖｔ)的距离需要的时间等于(ｔK2 －ｔK1 )，所以
在动系统中，光通过
距离（杆的相对长度）需要时间等于（ｔA2
－ｔA ） ，所以
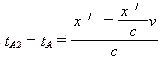
将上述二式代入（1）得到
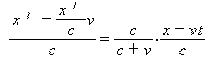
２、时间从静系统到匀速平移系统的变换
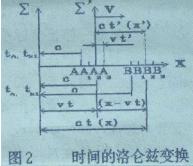
由公式(1)我们来研究(ｔA2－ｔA )的另一表达方式。在图２中，动钟Ａ由Ａ2 位置运动到Ａ3 位置，其距离可以表示成 (ｃｔ－ｖｔ)－(ｃｔ′－ｖｔ′)。其中ｔ是静系时间，ｔ′是动系时间。动坐标Σ′(或Ａ钟)以速度ｖ移动这段距离所需要的时间就是观察者同时看到Ｂ钟、Ａ钟信息时ｔA2 与ｔA 的时间差，也就是表示杆的相对长度的相对时间。于是
|
|
 |
３、Ｙ轴坐标从静系统到匀速平移系统的变换
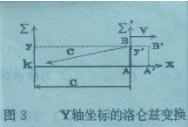
设空间有一静止参照系Σ和一运动参照系Σ′。动系以速度ｖ向Ｘ轴增加方向运动。在动系Ｙ轴上有刚杆AB，两端固联Ａ 钟与B钟。Ａ 钟位于动系原点，Ｂ 钟和Ａ钟相距ｙ′坐标，静系原点有 Ｋ 钟。如图３所示。
由于动钟Ａ和动钟Ｂ相对于静系都作相离运动，根据论文四《时空的绝对与相对》相离运动公式(４)我们同样得到
|
 |
然而，观察者看到Ｂ钟发来的光信息，在“斜着”向自己传来时，也看到这束光沿着Ｙ轴在“下降”。
在
走完了BK这段高度ｙ。于是
在随动系统一道运动的观察者看来，光“下降”ｙ′高度的同时，也走完了AK这段路程。因为动系以速度ｖ向Ｘ轴增加方向运动，光沿斜路程向静系原点运动，看起来光“下降”ｙ′高度的速度是（ｃ＋ｖ）。
于是
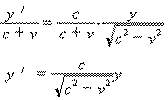
其中
同理，可以推得
现在我们把公式(ａ)、(ｂ)、(ｃ)、(ｄ)归并到一起
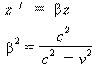
这就是洛仑兹变换的正确形式。
（二）、由动系看静系
上面我们是站在静系立埸看动系推导出洛仑兹变换新公式的。相反，如果站在动系立埸看静系，公式
| (３)是否适用呢？站在动系看静系和站在静系看动系 属于第一类镜像对称问题，物理规律相同，洛仑兹变换也 相同，我们必须证明。 如图４所示。设空间有一个静系Σ和一个动系Σ′， 动系以速度ｖ向右运动，相对地动系原点Ｋ钟处的观察者 认为自己是“静止”的，他看到Σ以速度ｖ向左运动。静 系中有杆ＡＢ，两端固有Ａ钟和Ｂ钟。 |
 |
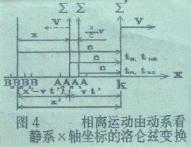某时刻由Ａ钟和Ｂ钟向Ｋ发出光。Ａ钟光信息到达观察者时，观察者看到Ｋ钟指示 ｔK1 ，Ａ钟指示ｔA，这时Ａ钟和Ｂ钟已分别“运动”到Ａ1 和Ｂ1 。当Ａ钟在Ａ2 位置发出的光和Ｂ钟发出的光同时到达观察者时， 观察者看到Ｋ钟指示ｔK2 ，Ａ钟指示ｔA2 ，Ｂ钟指示ｔB ＝ｔA2 。根据论文四《时空的绝对与相对》相离运动公式（５）：
注意到我们现在是站在动系看静系，这里钟的命名参数不同，我们得到
由图４我们看出，在(tA2 －tA )时间内，光在Σ′中光程为(x′－vt′)。在(tK2 －tK1 ) 时间内，光在Σ中光程为(x＋x·ｖ／c ) 。于是
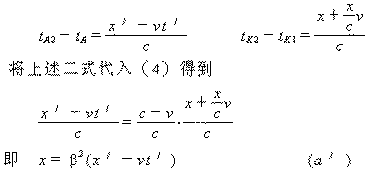
公式(ａ′)与公式(ａ)具有相同的形式。
同理，可以导出Ｙ轴、Ｚ轴和时间的变换公式，它们和公式（３）形式上一致。
我们得出结论：从动系统看静系统和从静系统看动系统，对于洛仑兹变换来说是等价的。即物理规律对相互作匀速平移运动的参照系来说，形式不变，这就是“相对性原理”。我们这里，“相对性原理” 是作为光速恒定原理的推论得出的。
虽然，由静系Σ看动系Σ′，动系钟以每秒 ｖ／(c＋v)的比例变慢，而由动系Σ′看静系Σ ，静系钟以每秒ｖ／ｃ 的比例变得更慢。但是，由于真正运动的是观察者，光由光源发出后，到达观察者要通过更长的空间距离。钟变得更慢和光程更长的效应正好抵消。因此，由静系看动系和由动系看静系，变换公式形式还是一致的。
二、相向运动洛仑兹变换公式的推导
本文到此为止都是以相离运动为基础推导洛仑兹变换新公式的。相离运动，时钟变慢；相向运动，时钟变快。现在我们根据相向运动时钟变快，来推导相向运动的洛仑兹变换公式。
（一）、两种镜像对称
空间反演具有两种镜像对称。第一种镜像对称取镜像对称系数Ｋ1
＝±１； 第二种镜像对称取镜像对称系数
相向运动和相离运动的对称性属于第二类镜像对称，
物理规律相同，洛仑兹变换不同，并由此导出杆长的表示，在相离运动中为
| ｘ′ ＝ｘ－ｖｔ， 在相向运动中为 ｘ′ ＝ｘ－ｉｖｔ． （二）、相向运动变换公式的推导 |
 |
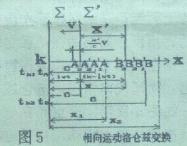如图５所示，某时刻由Ａ钟和Ｂ钟向Ｋ发出光，Ａ钟
光信息先到达，观察者看到Ｋ钟指示ｔK1 ，Ａ 钟指示ｔA 。
当Ａ钟在Ａ2 位置发出的光与Ｂ 钟在Ｂ位置发出的光同时
到达时，观察者看到Ｋ钟指示ｔK2 ，Ａ钟指示ｔA2 ，Ｂ钟
指示ｔB＝ｔA2 ，根据论文四《时空的绝对与相对》相向运动公式(６)，我们得到
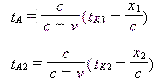
两式相减并考虑到这是相向运动公式，利用镜像对称系数ｉ，得
在相对时间(tA2 －tA )内，相对光程为
在绝对时间(tK2－tK1 )内，光程为( x－i v t )。 代入式（５）得
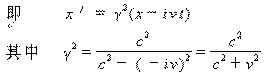
如果我们利用论文四《时空的绝对与相对》相向运动公式(７) ，可以得到
（6）
从式(６)出发，能推导出站在动系Σ′立场看静系Σ的变换，它和式(５)形式相同，两系统是等价的。
同理，可以推导出Ｙ轴、Ｚ轴和时间ｔ的变换。于是我们得到相向运动时的洛仑兹变换：
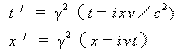
其中
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑
