物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-洛仑兹变换新公式的应用（Ａ）（洛仑兹变换新公式在运动学中的运用）

《二十世纪物理学批判》第一篇
论文九

洛仑兹变换新公式的应用（Ａ）
（洛仑兹变换新公式在运动学中的运用）

吴家荣

内容提要:把洛仑兹变换新公式应用到运动学和动力学中，我们将能建立一个符合唯物辩证法的相对论。在运动学中，相离运动“尺缩钟慢”；相向运动“尺胀钟快”。阐明了速度合成的相对性――爱因斯坦速度合成公式和速度合成的绝对性――伽里略速度合成公式之间的关系。并从多种角度对“麦克尔逊――莫雷实验”做出新的解释。

关键词　　双生子佯谬　　麦克尔逊――莫雷实验　　速度合成　　速度变换

    洛仑兹变换有两种截然不同的形式，一种适用于相离运动；另一种适用于相向运动。对于物理规律这两种形式的洛仑兹变换结论相同；对于现象它会导致不同的结论，但却符合经验和理性，我们必须重新考察和评价以往的实验。

    以下，我们仅以相离运动为基础来考察，之于相向运动除现象不同外，对于规律两者结论完全相同，这在论文一《共轭洛仑兹变换》中我们已经举了几个例子。为了行文简单起见，我们这里就不再考察相向运动的情况了。

    适用于相离运动的洛仑兹变换新公式为

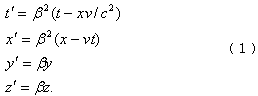
一、球面波在动、静两个系统中的变换

    设有一个“静止”参照系∑和一个相对于∑以速度v作匀速平移运动的参照系∑′。当t′＝ t ＝０时，即这两个系统原点重合的这一时刻，令一球面波从原点处发射，并在系统∑′中以速度c传播，假如（x′，y′，z′，t′）是这个波在动系统中刚刚到达的一个时空点，则

    是球面波在动系统∑′中的运动方程。

    现在用新的洛仑兹变换公式（１）变换

于是我们得到

    因此，在动系统看来以速度c传播的球面波；在静系统看来，这个波仍然是具有传播速度c的球面波。这和用经典洛仑兹变换公式来变换，具有相同的结果。

    由光速恒定原理，我们推出洛仑兹变换。这里，我们又由洛仑兹变换，获得“物理定律，在两个相互作匀速平移运动的坐标系中，形式不变”的结论。因而相对性原理的这种表述可以作为光速恒定原理的推论。但必须注意，惯性系是不是等价的，要看我们站在什么立场看问题。是相互考察还是分别考察。

二、运动物体的形状在动、静两个系统中的变化

    让我们观察在运动系统∑中相对静止的一个球状物体，其半径为Ｒ，球心位于∑′的坐标原点，相对于静系统∑以速度v运动的这个球，其表面的方程是

    因为是表面方程，不是运动方程，与时间t无关。所以用我们的变换方程式（１）来变换这个方程，在动、静两系统中，就会有不同的表述。设t＝０，用x，y，z表示这个球的方程时，则是

或  

    因此，在静止状态下测量为球状的物体，当处于运动状态时，在静系统看来，就具有扁平椭球的形状，其三轴为

    爱因斯坦在狭义相对论著作《论动体的电动力学》中说：

    “球（因而无论任何形状的刚体也一样）在Ｙ、Ｚ方向上的尺寸，看来不因运动而有所改变；但在Ｘ的尺寸看来则按的比率缩短了。”［１］

    根据我们的变换公式所推导的结果，应该是球在Ｙ、Ｚ轴方向上的尺寸也缩短了，缩短的比率是而在Ｘ轴方向上的尺寸是按的比率缩短的。

三、运动钟在动、静两个系统中的变化

    为了对比，我们把爱因斯坦著作中的一段引在这里：“让我们想象有这样一些钟：当它们相对于静系统不动时，能用来指示时间t；而当它们相对于动系统静止时，能用来指示时间τ。设把其中一只钟放在Ｋ的坐标原点上，把它调整好，使它指示时间τ。从静系统看来此钟的快慢如何？

    与钟的位置有关的量x，t与τ之间，显然有下列关系：

所以

    由此可见，这钟所指示的时间（在静系统看来）每秒慢秒或者略去四阶以上的量，则慢秒。

    由此就产生了以下异乎寻常的结果，假定在Ｋ中Ａ，Ｂ两点各有一只静止钟，在系统看来，这两只钟是同步的；如果Ａ点的钟以速度v沿ＡＢ线向Ｂ点运动，那么当它到达Ｂ点时，这两只钟就不同步了，从Ａ到Ｂ的钟，比另一只甾在Ｂ点的钟慢了（准确到四阶量），其中t是这只钟从Ａ到Ｂ所费的时间。

    立刻可以看出，假如钟沿任何多边形的边从Ａ运动到Ｂ，甚至Ａ点与Ｂ点重合，上述结论仍然有效。

    如果我们假定，在多边形的场合已经证实的结论，对连续曲线来说是有效的，那么就会得出下述结论：如果在Ａ点有两只同步的钟，其中一只沿着闭合曲线以恒定速度，经过t秒后回到Ａ。这样，当这只钟回到Ａ点时，比保持静止的秒。由此得出结论：当其他条件完全相同，在赤道的平衡轮钟，比起放在两极的完全一样的钟走得慢一些，不过慢很小的数值。”［２］

    爱因斯坦这里的结论很明确：运动钟真的变慢了！这与爱因斯坦的规定：

    “我们进一步设想，在杆的两端Ａ与Ｂ各放置一只钟，它们与静系统的钟是同步的，也就是说，在任一瞬时，这两只钟的指针位置对应于它们碰巧所在之处的‘静系统时间’。所以这两只钟也是‘在静系统中同步’的。”［３］明显矛盾。

    根据本文给出的洛仑兹变换新公式（１），我们将得到完全不同的结论。

因为  

将   

得   

    这就是说，动钟Ａ与它所到之处的静钟是“同时同步”的，因而也与静系原点处的Ｋ钟是“同时同步”的。这就与引文［３］不相矛盾了。既然运动钟没有“真的”变慢，那么“时钟佯谬”或者“双生子佯谬”的难题，也就得到了澄清。那么通常对“时钟佯谬”的解释错在哪里呢？所谓“时钟佯谬”是这样的：

    我们设想甲、乙是一对孪生弟兄。他们计划做一次高速飞船旅行，来检验一下狭义相对论。甲甾在发射基地，乙周游天外。当飞船再度回到基地时，是甲比乙年轻，还是乙比甲年轻？这里有两种答案：（１），甲看乙船上的钟变慢了，所以，甲说乙年轻些；（２），乙看基地上的钟变慢了，所以，乙说甲应该比他更年轻一些。在这两难的境地，运动钟变慢的结论，到底应当怎么办？这是个有名的疑难，叫做“时钟佯谬”或“双生子佯谬”。

    按照运动钟变慢的理论，甲看乙钟变慢，乙看甲钟变慢这种对称性，只有当甲和乙的相对运动速度不变时，才能保持。或者说，只有互相作匀速直线运动的两个惯性参考系，互相之间才是等价的。一旦出现了变速的相对运动，就不能使用这种对称性了。通常认为，甲和乙都生活在宇宙间，他们周围还有大量的天体。因此，双生子问题中有三个因素：甲、乙和他们周围的宇宙。如果甲甾在基地上，他相对于大量天体并没有做变速运动，在甲看来，只有乙在做变速运动。在乙看来，情况与甲不同。他不但看到甲在做变速运动，而且整个宇宙都在做变速运动。一边是整个周围的宇宙，一边只是一个飞船，这是明显的不对称性。所以由对称性引起的两难是不存在的。［４］

    笔者认为这种解释是不能令人诚服的。狭义相对论是以相互作匀速运动的系统为研究对象的，如果要借助第三个系统才能判别，这就等于承认了“绝对标准”的存在，这与爱因斯坦的相对论相抵触。爱因斯坦和他的追随者们认为，一切都是相对的，没有“绝对标准”。他们自认为比牛顿高明，简直是胡说八道。何况我们已经论述过，火箭的加速系统，并非“惯性系统性质”的加速系统，这与爱因斯坦的那个相对论简直是“风、马、牛”不相及了。

    实际上相互作匀速直线运动的两个参照系是能够区别究竟是哪个在运动，哪个是“静止”的。或者说，哪个运动的更快一些。如果他们同向运动一样快，这已经是相对静止了。

    当x＝v t时，动钟Ａ与静系原点处静钟Ｋ作相离运动时，动钟Ａ的状态由下式描述：

    （为了简单起见，我们仅考虑动钟Ａ沿Ｘ轴方向运动）

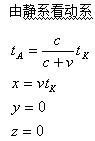
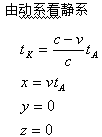
    当动钟Ａ与静钟Ｋ相向运动时，钟的状态应由下式描述：

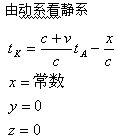
    其中：x为计时开始时，动钟Ａ与静钟Ｋ之间的距离。

    仰望天空，在距离相等，即半径Ｘ相同的天球面上的钟，在观察者视野之内，能够同时看到的话，它们都是彼此“同时同步”的。而和观察者身边的钟相比，是“同步不同时”的。始终慢x/c秒。不管这些钟是静止的还是运动的（变速状态亦然，但不能脱离半径为Ｘ的球面）。

    观察时间的相对性，由于光速恒定，归根结底是与空间距离有关。匀速平移改变了观察者与空间事件的距离；直线加速只是更快地改变了观察者与空间事件的距离。只要距离不改变，观察时间的相对性就不会变化。距离Ｘ一定，动钟与静钟“同步不同时”，始终慢x/c秒，距离越远，越不同时。

    相离运动，动钟与静钟“既不同时也不同步”，速度越快，钟走得越慢。

    动钟与它们所到之处的静钟总是“同时同步”的。时间的流逝是绝对的，观察时间的流逝是相对的。

四、关于麦克尔逊――莫雷实验

（一）、从运动立场来看杆长的绝对性

    在论文四《时空的绝对与相对》中我们已经讨论过长度的绝对性，但那是站在“静止”系统的立场，看到的运动杆长的绝对性。其特征量是静钟Ｋ的本钟时间差。

    现在我们来讨论站在运动的立场上来看动杆的长度。设空间有一动杆ＡＢ，以速度v作匀速平移运动，在杆ＡＢ的两端各有一只爱因斯坦钟。令一束光在t_A离开Ａ，于时刻tＢ在Ｂ点被反射，在时刻t_A′再返回到Ａ。根据光速恒定原理，光由动钟Ａ发射后，仍以速度c向Ｂ传递，与钟的运动无关。但杆ＡＢ确在运动。于是我们根据爱因斯坦的推导有

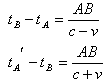
    这样，爱因斯坦说，随着动杆一起运动的观察者就会发现，这两个钟是不同步的。［５］

    然而，这实质上还是从静系看动杆。若从动系看动杆，根据相对性原理，观察者并不知道自己在运动，他认为自己是静止的。因而由动系测量仍然是

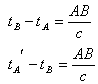
    即，杆在运动中光线来回的时间和杆在“静止”时来回的时间，情况完全相同

    就是杆的绝对长度。

    这就回到了爱因斯坦绝对同时性定义：否则，根据爱因斯坦相对论观点，没有绝对静止，“静止”本身也在运动。那么爱因斯坦的两个关系式

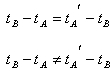
    必有一个不能成立。

（二）、从运动的立场（即测量者随仪器一同运动）来看麦克尔逊――莫雷实验

    图１是麦克尔逊――莫雷实验的示意图。Ｌ为仪器互相垂直的两臂长度，因测量者和杆是相对静止的，测量者测得与地球运动方向一致的臂，光来回需要的时间为

(2)     测量者测得与地球运动方向垂直的臂，光来回需要的时间也是               (3)

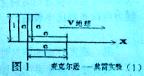    这样，我们就明白了为什么麦克尔逊――莫雷实验干涉条纹不发生位移，因为根本就没有时间差。

（三）、从“静止”的立场来设想麦克尔逊――莫雷实验

    这里使用设想一词，是因为麦克尔逊――莫雷实验总是处于运动状态进行的，测量者必须和仪器一道运

动。为了理解这一实验的否定结果，我们不妨从“静止”的立场来设想一下。如图２所示，Ｌ为仪器的互相垂直、等长的两臂绝对长度，即不论是在静止状态测量，还是在运动状态测量都是Ｌ。     首先，我们研究由∑系统看来，光在∑′系统沿Ｘ轴方 向一个来回需要多少时间？

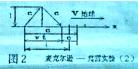静止的观察者看到的结果应是杆长在Ｘ轴方向缩短了，而他看到的光通过这段距离所需要的时间是t₁。
根据本文给出的洛仑兹变换新公式（１），我们得到，光发射出去的光程为

    根据光速恒定原理，光在动系中的速度是c，我们来确定相对时间t₁

因为   

所以   

光在在回来时，光程为

同理，我们得到

光在Ｘ轴方向传递，在“静止”的观察者看来，一个来回总共用的时间为

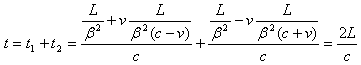                 (4)

其次，我们再研究光在Ｙ轴方向（垂直于速度v方向），一个来回所需要的时间是多少？

观察者看到，光沿Ｙ轴方向走的是斜线。发出的光与反射回来的光，光程相等，都是

        

根据光速恒定原理，我们来确定光走完这段光程的相对时间：

因为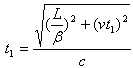   

所以   

这样，我们得到光在Ｙ轴传递，一个来回总共用的时间为

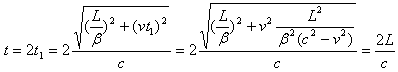           (5)

根据式（４）、（５），多们同样得到，在“静止”的观察者看来，因为同样没有时间差，光的干涉条纹位移实验是做不成的。

    另外，根据式（２）、（３）、（４）、（５）我们得到下述结论：

    不论杆是在“静止”的状态测量，还是在运动的状态测量；不论杆是与运动方向一致，还是与运动方向垂直，其绝对长度是不变的。而观察杆长的相对性，无论是在运动的方向上，还是在与运动垂直的方向上，都受到运动速度的影响。在Ｘ轴方向以β２的比率收缩，在Ｙ轴方向以β的比率收缩。

五、速度合成的相对性――爱因斯坦速度合成公式

    设有一个静止系统∑和一个运动系统∑′。动系统以速度v沿静系Ｘ轴增加方向运动。令动系中有一质点，相对于动系∑′也运动。满足下列运动参数方程

    其中　Ｕx′和Ｕy′为常数，是质点运动速度Ｕ在动系Ｘ′轴和Ｙ′轴上的分量。

    求这个质点相对于静系统∑的运动。我们用公式（１）把质点在动系统∑′中用x′，y′，z′，t′表示的运动参数方程，变换到静系统∑中用x，y，z，t表示的运动参数方程。

    因为   

    所以   

    因为   

    所以   

    于是   

同理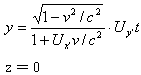

    我们令

    其中　α是速度u和v之间的夹角。

    因为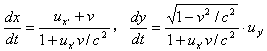 

    所以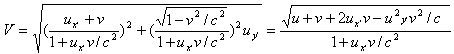  

    又因为  

    于是             (6)

    式（６）就是速度合成的一般公式。

    当α＝０°时，即u和v一样也取Ｘ轴方向，我们得到

                                       (7)

    当α＝９０°时，即u和v相互垂直，u取Ｙ轴方向，我们得到

                             (8)

    由式（７）、（８）我们看到通常的速度合成公式仅对第一级近似有效。或者说，当v＝０或c＝∞时，我们将看到一个绝对世界。

（一）、两个小于光速的速度合成在静止的观察者看来合速度仍然小于光速

    若令 v＝c－a，u＝c－b；a与b取小于c的正值，则

    由式（７）有

由式（８）有

（二）、光速恒定，与任何速度合成在静系观察者看来仍然是光速

    由式（７）令u＝c，（当α＝０°，在Ｘ轴方向），则有

    由式（８）令u＝c，（当α＝９０°，在Ｙ轴方向），则有

    这样我们看到光无论在运动速度方向，还是垂直于运动速度方向，合成的结果，仍然是光速。并且，不论速度v是小于光速还是超光速。

    一般地当α为任意角时，由式（６）也能得到光速c进行速度合成的结果仍然是c。令u＝c则（６）式变为

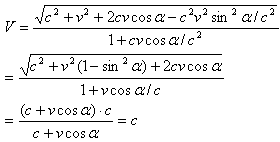
（三）、大于光速c的速度与参照系速度v合成，在静止的观察者看来合速度大于c

    由式（６），令u＝k c ( k＞1 )，则

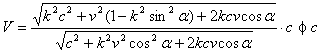
    上述（一）、（二）、（三）的结果，从数学上证明了我对时空因果律的分析是正确的。同时也说明了数学的伟力，数学是能够描述物理世界的。离开严密的数学推导，是否定不了爱因斯坦的那个相对论的。

    （六）、速度合成的绝对性――伽里略速度合成公式

    上述第五点中的速度合成公式在推导过程中，我们使用了洛仑兹变换，因而那是相对性速度合成公式，即两个惯性参考系相互考察时所看到的情形。如果就一个参考系而言，无论是静系还是动系，速度的合成应是绝对的。这里我们不能“看”，一“看”，通过光架起的桥梁，我们就又回到了相对观察。但是我们可以“想”，它一定满足伽里略速度合成公式。因为心“想”的速度可以无穷大。令c＝∞时，则公式（６）、（７）、（８）变为

              (9)

    伽里略速度合成公式允许合速度超过光速。

    光由静止的光源发射速度为c。光由运动的光源发射，由静止的观察者看来速度也是c。但我们可以想到，合速度一定是c＋v＞c。由于观察者随动系一同运动，所以由动系测量光速仍然是c。通常所说的光速是指光的波速，并非光子的运动速度。这和水的波速与水分子的运动速度，以及电的波速与电子的运动速度道理是一样的。只不过是，光子本身的运动速度也是c，比它们大一点而已。

    为了更清楚地说明由运动光源发射的光，按照伽里略绝对速度合成观点来看，合速度为（c±v），即发射的光子与光源运动方向相同时为（c＋v），发射的光子与光源运动方向相反时为（c－v）。我们再来看麦克尔逊――莫雷实验。这次我们以绝对的观点来考虑。见图２，杆的绝对长度为Ｌ，光发射出去的绝对速度为c＋v，需要的时间为t₁，则光程为Ｌ＋vt₁；光反射回来的绝对速度为c－v，需要时间为t₂，则光程为Ｌ－vt₂。先看Ｘ轴方向，我们有

                            (10)

                           (11)

由式（１０）、（１１）解得

则有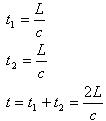                     

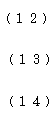
再看Ｙ轴方向，我们有

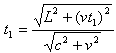                          (15)

解得                               (16)

则                            (17)

    由式（１４）和（１７），我们看出麦克尔逊――莫雷实验仍然是否定结果。

    把式（１２）、（１３）、（１６）和式（２）、（３）比较一下，我们会发现，当惯性系分别考察时动系和静系是等价的，我们完全可以把任何动系看成静系。而由式（４）、（５）知道，当惯性系相互考察时是不等价的，必须使用洛仑兹变换，才能获得惯性系对于物理规律的等价性。

七、速度的变换

    为物体相对于∑的速度分量。设∑′相对于∑沿Ｘ轴方向以速度v运动。现用洛仑兹变换式（１），先求Ｘ轴分量，因为

    两式微分

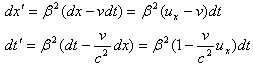
    两式相除得

                                (18)

    同理                      (19)

                               (20)

关于这组公式的物理意义，我们在下篇论文《洛仑兹变换新公式的应用（Ｂ）》中还要阐述。

［１］爱因斯坦，“论动体的电动力学”，《相对论原理》，第４１页，科学出版社，1980年。
［２］爱因斯坦，“论动体的电动力学”，《相对论原理》，第４２页，科学出版社，1980年。
［３］爱因斯坦，“论动体的电动力学”，《相对论原理》，第３５页，科学出版社，1980年。
［４］方励之，褚耀泉《从牛顿定律到爱因斯坦相对论》，第４８页，科学出版社，1980年。
［５］爱因斯坦，“论动体的电动力学”，《相对论原理》，第３６页，科学出版社，1980年。

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页