物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-洛仑兹变换新公式的应用（B）（用洛仑兹变换新公式考察动力学几个问题）
《二十世纪物理学批判》第一篇
论文十
洛仑兹变换新公式的应用（B）
（用洛仑兹变换新公式考察动力学几个问题）
吴家荣
内容提要:把洛仑兹变换新公式应用到运动学和动力学中，我们将能建立一个符合唯物辩证法的相对论。在动力学中，相离运动质、能增加；相向运动质、能减小。根据洛仑兹变换新公式阐明了多普勒效应和康普顿效应，并由不同的途径推导出质能关系式 E=mc2。
关键词 质量、能量相对论效应 多普勒效应 康普顿效应 质能关系
洛仑兹变换有两种截然不同的形式，一种适用于相离运动；另一种适用于相向运动。对于物理规律这两种形式的洛仑兹变换结论相同；对于现象它会导致不同的结论，但却符合经验和理性，我们必须重新考察和评价以往的实验。
以下，我们仅以相离运动为基础来考察，之于相向运动除现象不同外，对于规律两者结论完全相同，这在论文一《共轭洛仑兹变换》中我们已经举了几个例子。为了行文简单起见，我们这里就不再考察相向运动的情况了。
适用于相离运动的洛仑兹变换新公式为
 |
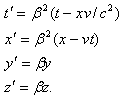(1) |
其中 
一、电磁场张量的变换
设电埸强度Ｅ和磁感强度Ｂ在三个坐标上的分量分别为（Ｅ1、Ｅ2、 Ｅ3）和（Ｂ1、Ｂ2、Ｂ3）。电磁场Ｅ和Ｂ用势表示为
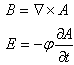
其分量为
 |
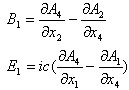(2) |
引入一个反对称四维张量
由（１）式可得，电磁场构成一个四维张量
 |
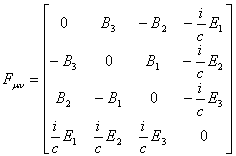(3) |
用电磁场张量我们可以把麦克斯韦方程写为明显的协变形式。这方程组中的一对方程
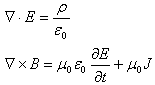
可合写为
另一对方程
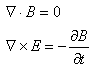
可合写为
由张量变换关系
根据洛仑兹变换新公式（１）我们有变换矩阵
 |
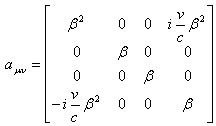(4) |
利用式（３）、（４）可得电磁场变换关系
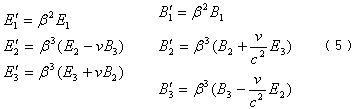
上式可以写成更为紧致的形式
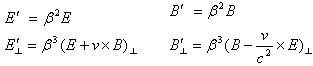
式中和⊥分别表示与相对速度v平行和垂直的分量。
电场和磁场统一为四维张量，反映出电磁场的统一性和相对性。电场和磁场是一种物质的两个方面。在给定参照系中，电场和磁场表现出不同性质，但是当参照系变换时，它们可以互相转化。例如，在某参考系上观察一个“静止”电荷，它只激发静电场和自旋电荷的静磁场，只要用标势φ描述，但是变换到另一参考系时，电荷是运动的，除了静电场和静磁场的运动之外，还有运流电荷的动磁场，必须同时用Ａ和φ描述。
二、加速度的变换
设带电粒子在静电场中由速度v开始，它相对于动系统∑′是静止的。在以后的过程中，它将获得电场的加速。设在动系∑′中的加速度为
我们把加速度由动系统变换到“静”系统。根据适用于相离运动的洛仑兹变换新公式
分别求一阶导数，二阶导数，再运用参数方程的求导公式我们得到
三、带电粒子在电磁场中运动的绝对质量和相对质量
首先我们考虑有质动力Ｆ作用下的情况。由洛仑兹变换新公式及论文一《共轭洛仑兹变换》公式（１１）我们有
根据牛顿定律，由式（６）、（７）可得
和
于是我们得到
(9)
这个结果和质量是标量，在两个匀速平移运动的惯性系中应该恒等是并不矛盾的。
其次我们来看在电磁场力的作用下情况怎样。电场和磁场虽说可以统一，但它们毕竟不是完全对称的。
设带电粒子的电荷为Ｑ，以速度v在静电场Ｅ中运动。从动系∑′看来，电荷相对静止，仅有静电场，其质量为
现在我们用（５）、（６）把式（１０）由∑′变回到∑。并注意到，运动电荷由∑系统看来是受电场力和磁场力共同作用的。我们得到
即由静系的观察者看来运动电荷的
(12)
由式（１１）我们看到，带电粒子在电场中运动，在沿运动速度方向上，相对质量等于绝对质量。而在与运动速度垂直的方向上，相对质量等于绝对质量的
。该相对质量仅仅是观察的后果，所谓带电粒子在其运动方向上的电磁质量是不存在的。
既然物质的质量不随运动速度而改变，那么物质运动的速度就可能超光速，只要有足够大的力和足够充分的力的作用时间。当运动物质的速度超过光速时，论文九中的速度合成公式（８）、（９）、（１０）仍然有效。说明光信号传递的速度，由静系的观察者看来仍不会变化，正如高速航行的快艇，水波的速度不变一样。当然，和物质一同运动的光子本身是超光速的，恰如高速快艇船体上粘附的水珠一样是超波速的。
以２倍光速相离而去的钟，其时间看起来是
目前我们还没有发现质量小于“光子”的物质，因而也难于发现超光速的物质运动。
若我们把式（１０），根据：力＝质量×加速度，作如下变形
则当我们依靠光测量加速度和力时，如果忽略了β２或β的影响，就会出现
(14)
把式（１２）、（１３）、（１４）结合起来考虑，我们会得出下述结果：
在有质动力作用下，可以看到
纵质量＝横质量＝m
在电磁力作用下，可能看到
纵质量＝m
也可能看到
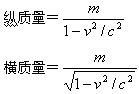
总之，我们通过视觉或用与光有关的手段来认识世界，只能认识物质运动的形状、位置、速度以及它们与光传播方向之间的关系。光是不能传递质量大小的信息的。要获得质量大小的认识必须借助其它手段。凡是利用视觉和与光有关的手段来认识质量，总是要通过速度、距离、时间的平均值来折算，这就会造成我们认识质量的相对性（错觉）。
四、带电粒子运动的动能增量
带电粒子的动能增量与电场对它所做的功有关。设带电粒子为单位电荷q，电场的功为Ｗ，带电粒子沿Ｘ轴方向以速度v运动，处于动系∑′原点上。
从动系∑′看，因为带电粒子相对于∑′速度为零，所以电场力的功为
(15)
从静系∑用绝对观点看问题，电场力做功，所以电场的功为
(16)
从静系∑用相对观点看问题，功是多少呢？观察者看到是相对电场力在对粒子做功
于是 
(17)
公式（１７）忽略四阶以上的量就是
这和式（１６）是一致的。式（１７）对有质物体也有效。
与上述三种电场力的功相联系的动能增量分别为
(18)
(为什么动能具有mv2的形式，作者将在本论文集第二篇中详细论述。实际上这就是惠更斯，莱布尼兹所称的活力)［１］［２］。
在论文八《洛仑兹变换的物理意义》中我们曾多次提到“虚幻”、“幻影”。但物理学是以观察和测量为基础的，我们有句俗话，叫做“眼见为实”，因此，我们往往把看到的情景当作真的是这样。例如距我们１００光年的某星球上，假如有生物存在，我们现在“看”到他们正在打仗，大家都会仰起头来观看这场战争，虽然我们可以想到那是１００年前发生在那颗星球上的事件，似是而非根据“眼见为实”的立场，有人就会认为他们现在还在打。
如果我们要进行动能的绝对计算的话，我们都用（１８）式的第二式。如果我们真的能“看见”运动物体的动能，那应该是（１８）式的第三式所表示的。
五、从运动物体的总能量推导出质能关系式
（一）、动系与静系时间的流逝是同步的
由洛仑兹变换新公式（１），我们来推导动系绝对时间差和静系绝对时间差的关系。
因为 
取微分 
于是得到
(19)
这就是说时间的流逝是绝对的，静钟和动钟实际上是同步的，虽然他们可以不同时。
（二）、四维速度矢量
现在我们来研究四维速度矢量。因物体的位移dxμ为四维，dt′为标量，由式（１９），dt′＝dt，所以
（20）
是一个四维矢量。这个四维矢量称为四维速度矢量，其分量为
（21）
参考系变化时，四维速度有变换关系
（22）
式中 aμν按本文给出的（４）式取值，即
（23）
现在我们必须回答，我们在论文九《洛仑兹变换在运动学中的应用（Ａ）》中导出的速度变换公式（１８）、（１９）、（２０）它们在形式上不同于洛仑兹变换，这不矛盾吗？
不矛盾。因为式（２３）中的Ｕ（∑′）和那里的Ｕ′是有区别的。那里的Ｕ′是按照
定义在∑′系中的。实际上v代表坐标原点的速度，它有自己的“虚幻”位置，u代表（x－vt）点的，它也有自己的“虚幻”位置。即使u＝v我们看到的u′也不v′。因为这两个速度之间有空间距离（x－vt），应符合“速度相同，位置不同”的惯性系选择的惟一性定理。当我们按照“动系∑′的惟一性原理”考虑时，它们都符合
而当我们硬要把u放到v点的“虚幻”坐标系中考虑时，则得到论文九中式（１８）、（１９）、（２０）不符合洛仑兹变换的一组关系式。这再次证明了从相对的观点看，惯性系绝非都是等价的。
（三）、四维动量矢量
经典力学的基本规律是牛顿定律：
式中 Ｆ是作用于物体上的力
P是物体的动量。
在经典力学中，设物体的质量为m，运动速度为v，则它的动量为m v。设四维动量矢量为pμ，则
因为uμ是洛仑兹协变量，m是标量，所以pμ也是洛仑兹协变量。
（24）
式中 aμν按本文给出的式（４）取值。这个四维动量矢量的空间分量和时间分量为
（25）
（26）
由式（２６）我们看到，p4与物体的能量有关。我们可以把式（２５）、（２６）合写为
由pμ可构成四维不变量
（27）
（四）、运动物体的总能量
物体的能量可以由对物体所做的功率计算得出。在经典力学中，对物体所做的功率为
把式（２５）代入上式得
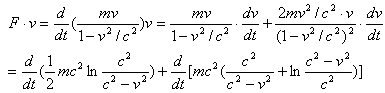
由于对物体所做的功率等于单位时间内对物体所做的功，所以功的表示为
（28）
式中
当V远小于C时，略去四阶以上的量，我们得到
（29）
在作者论文集《二十世纪物理学批判》第二篇《原子辐射的新观点》中，我们论证了与
的功相联系的动能具有
的形式，因而由（29）式我们得到运动物体的总能量为
（30）
式（３０）是在Ｖ远小于Ｃ的条件下得出的。当Ｖ远小于Ｃ时，运动物体的“虚幻”位置非常接近真实位置，因而式（３０）所描述的运动物体的总能量，就代表了运动物体能量的本来面目。
式（２８）中的第一项是与动能相联系的功，动能应具有下述形式
（31）
此动能表达式为相对观察的动能表达式，与式（１８）相同。将（３１）代入（２８）于是运动物体的总能量为
（32）
当Ｖ远小于Ｃ时，略去四阶以上的量，我们得到
（33）
式（３３）说明，运动物体的总能量，等于静能与动能之和。
当Ｖ＝０时，由（３２）或（３３）我们得到
（34）
这就是爱因斯坦导出的质能关系式，这是Ｖ＝０时的质能关系式，即物体“静止”时，所具有的全部能量。世间万物都在运动，相对的质能关系式应为式（３２），绝对的质能关系式应为（３０）或（３３）。
运动物体的总能量等于静能
之和，也可由下面看出：
由式（２７）在物体静止系统内，
因而不变量为
。因此运动物体的总能量由物体的能量、动量和质量关系式
可得 
（35）
由式（３５）我们可以看出，运动物体的总能量确实等于静能与动能之和。
由式（３５），当Ｖ＝０时，同样可得到关系式
下面两节我们从另一条途径推导质能关系式。
六、多普勒效应与光行差公式
设有一角频率为ω，波矢量为Ｋ的平面电磁波在真空中传播。在另一个参照系∑′上观察，该电磁波的频率和传播方向都会发生变化（多普勒效应和光行差效应）。以ω′和Ｋ′表示∑′上观察到的角频率和波矢量，现在我们研究Ｋ和ω如何变换。
设参考系∑和∑′的原点在时刻t＝t′＝０重合。设在该时刻，原点处的电磁波处于波峰，相位为０。在∑上周期t0之后，原点Ｘ＝０处于第二个波峰，相位为２π。在∑′上观察到第二个波峰出现的时空坐标为（x′，t′）它可由（x＝0，t＝t0）作洛仑兹变换求得，即在∑′上有
由此可见，电磁波的相位是一个不变量。一般说来，设在∑上观察，在空间某点Ｘ于时刻t，电磁场振荡有相位
这是一个物理事件。在另一个参考系∑′上观察这事件，设其空间坐标为（x′，t′），即在x′点于时刻t′，电磁场振荡有相位
由相位不变性有
但我们知道x与i ct合为四维矢量Ｘμ．因此，若Ｋ与
合为另一个四维矢量Ｋμ它们按四维矢量方式变换，有
由此我们得到一个四维矢量
Ｋμ的变换式为
其中 a μν按本文给出的公式（４）取值。
对沿Ｘ轴方向运动的洛仑兹变换（１）式有
 |
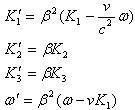（36） |
设波矢量Ｋ与Ｘ轴方向的夹角为θ，Ｋ′与Ｘ轴夹角为θ′有
代入式（３６）可解得
 |
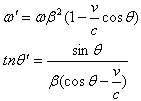（37） |
这就是多普勒效应和光行差公式。
从ω′的方程推出，如果一个频率为ν的光源以速度v作相离运动，则观察者接收到的光频率ν′由下列方程确定
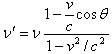（38）
当θ＝０时
（39）
可见，相离运动时频率红移。
若把电力或磁力的振幅按照在静系统或动系统测量，分别记作Ａ或Ａ′，则得到
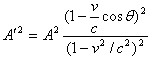（40）
当θ＝０时，这方程简化为
（41）
七、从物体的辐射推导出质能关系式
设有一列平面波以坐标系（x，y，z）为参照系时具有能量Ｅ。令光线的方向（波面法线）与系统的Ｘ轴间的夹角为θ。如果我们引入一个相对于系统（x，y，z）作匀速平移运动的新坐标系（x′，y′，z′），并令其坐标原点以速度v沿Ｘ轴运动，那么从系统（x′，y′，z′），测量时，这些光具有的能量是多少呢？
我们知道，光子的能量是
（42）
其中 h为普朗克常数；ν为光子的频率。
根据式（３８）、（４２）我们得到
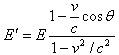（43）
当θ＝０时
假定静系统（x，y，z）有一个运动物体，以速度v沿静系Ｘ轴增加方向运动。设物体对静系统∑的能量为L0，对动系统∑′的能量为L0′，令这物体向与Ｘ轴成角θ的方向发射的能量为
的平面波，同时向相反方向发出等量的光。这样做的时候，物体对系统（x，y，z）保持v不变。因为是同一事件，它一定也适合于动系统（x′，y′，z′）。差别在于观察测量的值不同。考虑到向相反方向发射的光相对于观察者来说是相向运动了，发射出去的光质量其绝对速度已不是v，而是（c－v）。而相离发射的绝对速度是（c＋v）。
对于相向发射，因（c－v）﹤c，洛仑兹变换仍适用，考虑到第二类镜像对称系数i，我们有
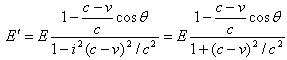
对于相离发射，因（c＋v）﹥c，正如我们在论文八《洛仑兹变换的物理意义》中所说，“即使有原因，也看不到结果”，洛仑兹变换公式已不适用。但我们知道，其绝对能量
是大小相等的，我们可以按照相向发射来处理。又因为发射方向相反，所以，对于相向发射取（c－v），对于相离发射取－（c－v）。
设在物体发射光之后的能量，在∑系统测量为Ｌ1，在∑′系统测量为Ｌ1′。则得到
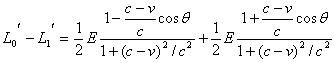
两式相减，得到
令（c－v）＝v，公式形式不变：
（44）
物体辐射，质量将减少。辐射的能量应等于辐射出去的物质所具有的动能。由式（３１）相对动能为
（正号为相向运动，负号为相离运动）于是有
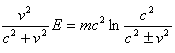
（45）
从这方程可以推出，如果一个物体以辐射的形式放出能量Ｅ，则其质量减少
（46）
式（４５）、（４６）略去四阶以上的量为
（47）
（48）
当Ｖ＝０时，
（49）
（50）
式（４９）是物体静止能量表达式，也就是质能关系式。
虽然运动不改变物体的质量，但辐射却改变物体的质量。由式（４８）和（５０）我们看出，辐射相等的能量，在静系∑的观察者看来，静止的物体辐射，辐射的质量多，运动的物体辐射需要的质量少。
所谓静能，是相对参照系静止的物体（Ｖ＝０）以辐射的方式将本身能量全部转化出去所具有的能量。
所谓运动物体的总能量，是指相对于参照系运动的物体（Ｖ≠０）以辐射的方式将本身能量全部转化出去，外加运动能量也随之转化出去，所具有的总能量。
在不考虑辐射的情况下，或者说物质没有发生核反应，没有以辐射的方式把自己全部转移掉，物体的能量就是其动能
其功的当量为
。
| 八、关于康普顿效应
这里公式推导与经典康普顿推导不同，不需要经典
设电子轨道运动速度为Ｖ０，与入射光子的夹角为φ， |
 |
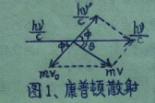为电子碰撞后的动量。从图中可以看出，散射波长与Ｖ0的大小和方向有关。Ｖ0越小，Φ越大，散射后的波长越长。
由动量守恒得
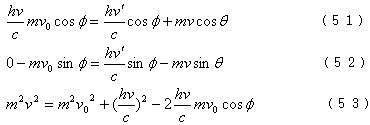
因为光作用于电子，将对电子做功，电子获得的功为［参见本文式（２９）］：
由功的守恒得（见作者本论文集第二篇《原子辐射的新观点》§3.2）
（54）
解（５１）、（５２）、（５３）、（５４）方程组：
将（５１）、（５２）变为
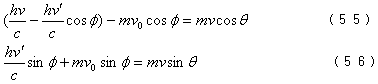
将（５５）、（５６）平方后相加得
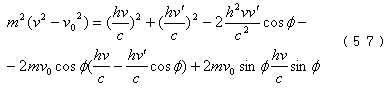
由式（５４）可得
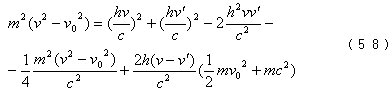
解（５７）、（５８）可得
 |
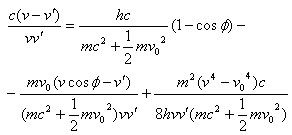（59） |
由（５３）式得
两边平方则得
 |
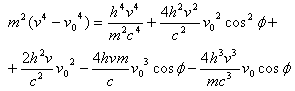（60） |
将式（６０）代入式（５９）得
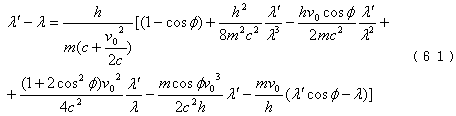
由式（６１）可知，散射波长与Ｖ0，Φ和λ都有关。
当电子轨道运动速度Ｖ0远小于Ｃ时，于是Ｖ0≈０，并且
我们得到
（62）
这就是经典康普顿公式。
实际上原子中内层轨道电子运动的速度很大，不能视为零。当观察角Φ一定时，因为电子轨道运动的线速度Ｖ0不同，所以实际观察到的散射波长不是单值，而有一宽度分布。
因为波长的改变还与入射波长有关，因此伦琴射线愈硬，即波长愈短，则波长增大的百分比愈大，因而能量损失的百分比就愈大。
［１］、思格斯，《自然辩证法》，第７０页，人民出版社，１９７１年。
［２］、《高中物理》第一册，第１１８页，人民教育出版社，１９９２年。
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑
为入射Ｘ射线光子的动量， 
为原子
为光子碰撞后的动量， 