物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-空间反演的两类对称性

《二十世纪物理学批判》 第一篇  论文三

空间反演的两类对称性

吴　家　荣

内容提要

　　虚数i 的数学意义我们都很清楚。本论文通过对两类空间反演对称性的论述，阐明了洛仑兹变换新公式中出现虚数单位ｉ的物理意义；为相互共轭的两组洛仑兹变换新公式的并存提供了依据。
关键词：　虚数ｉ　　物理意义　　两类镜像对称

一、什么叫相离运动，什么叫相向运动？

　　相离运动和相向运动都是比较而言，它们都是相对于静系统而言的，否则就无法判别。

　　如图１所示，Σ为静系统，Σ′为动系统以速度ｖ沿Ｘ轴增大方向运动。Σ″也是动系统以速度ｖ沿Ｘ轴负方向运动。Σ″构成了Σ′的镜像。相离运动（包括静系统、镜像系统）构成了洛仑兹群，洛仑兹变换公式

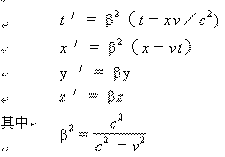
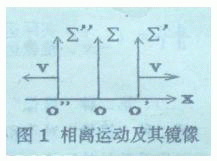
适用于此群。

　　如图２所示，Σ为静系统，Σ′为动系统，在Ｘ轴的正侧，沿Ｘ轴减小的方向以速度ｖ向静系统原点Ｏ处观察者运动，Σ″是Σ′的镜像。相向运动（包括静系统、镜像系统）构成了共轭洛仑兹群，洛仑兹变换公式

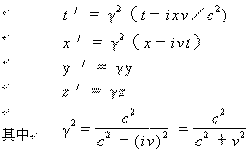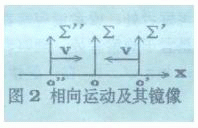适用于此群。

二、两种镜像对称 　　如图３所示，ＡＢ是一相对于静系统以速度ｖ向Ｘ轴 增大方向运动的杆。ｘ′＝ｘ－ｖｔ表示杆ＡＢ的长度。 这里ｘ′为常数，ｘ是ｔ的函数，可以写成ｘ（ｔ）。在 相离运动中，随着时间ｔ的流逝，ｖｔ增大，ｘ（ｔ）也 增大，保持ｘ′＝ｘ(ｔ)－ｖｔ值不变。

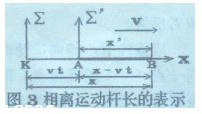流逝，ｖｔ增大，ｘ(ｔ)

减小。因此，用ｘ＇＝ｘ(ｔ)±ｖｔ的任何形式，都不能 表达杆长的不变。或者说，杆的长度ｘ＇不能同时用静系。 统参数ｘ，ｖ，ｔ表示出来。在图３中，ｘ和ｖｔ都是从 静系原点计量的，它们有共同的计量起点，而在图４中ｘ 从静系原点计量，ｖｔ却不是。这就是相离运动和相向运 动的区别。

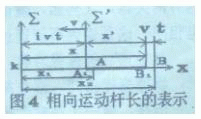　为了建立相向运动杆长和空间、时间、速度三者之间的联系，需要建立新的概念。

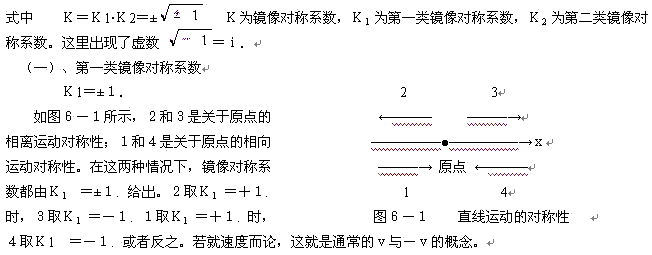
　　(一)、第一种镜像对称

　　我们知道，速度等于位移对时间的导数，空、时、速三者联系式为

                                          (1)

式中：　ｋ为常数，表示ｘ和ｖ的空间取向．ｋ＝±１．

　　这就是通常所说的空间反演对称性（或左右对称、镜像对称）。式(1) 中的ｋ＝±１称为镜像对称系数。

　　如图１、图２所示的相离运动或相向运动，观察者和镜子处于同一位置，即观察者处于对称中心．在这种情况下，无论是相离运动（图１）还是相向运动（图２），对称系数都是ｋ＝±１．实物运动取ｋ＝＋１时，镜像运动则取ｋ＝－１．或者反之。

　　因而，只要观察者处于对称中心（镜子位置），无论是相离运动的对称性还是相向运动的对称性，都有

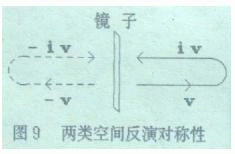
(二)、第二种“镜像”对称

第二种“镜像”对称和第一种镜像对称不同，所以， 镜像对称系数Ｋ的取值也不同。这第二种“镜像”对称正 是我们要建立的新概念． 　　如图５所示，对于观察者Ｋ来说Ａ的运动是相离运动； Ａ′ 的运动是相向运动．这也是一种镜像对称运动，但是 这和第一种镜像对称不同，第一种镜像对称是镜子必须置

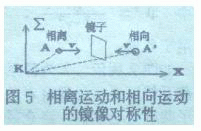于观察者处，或者说观察者必须处于对称中心。而这里相离运动和相向运动的对称性，镜子不是置于观察者处，观察者不在对称中心。为了区别这种情况，我们引入第二类镜像对称系数：在一般情况下，我们写成

                                  (3)

或者反之。

应该注意，相向运动时，ｘ和ｖｔ不是从同一点取值的，换成ｉｖｔ后，就可以和ｘ在同一点（ｖｔ的镜像点）取值了。这样，杆的长度ｘ′就可以和空间坐标ｘ，时间ｔ以及速度v建立联系了。由图４，我们得到

                      (4)

这和相离运动

具有第二类镜像对称的形式。

　　对于第一类镜像对称，K1＝±1，表示物质实际运动（实像）和镜像运动（虚像）之间的方向关系, （当然，镜像运动也是实际可以发生的）。此时，物理规律相同，洛仑兹变换也相同。这是爱因斯坦通过φ(v)＝φ(－v)证明了的。

    对于第二类镜像对称，表示物质相离运动和相向运动之间的方向关系。此时，物理规律相同，洛仑兹变换不同。

　　但是，就一个观察者来说，他看到一个物体运动，在某一时刻，要么是相离而去，要么是相向而来。因而总的格式应该如下

    归纳一下应有：

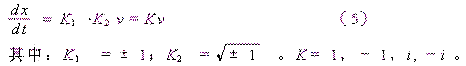
对应于K2　洛仑兹变换不同； 对应于K1　洛仑兹变换相同。见表１。

表１　　两类镜像对称公式的比较表

公 式 名 称	方 　 向	从静系Σ看动系Σ′	从动系Σ′看静系Σ
洛 仑 兹 变 换	相 离 运 动
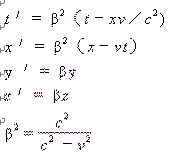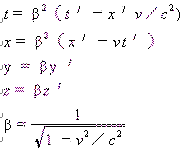	相 　 向 　 运 动

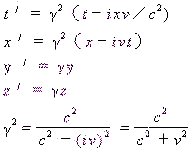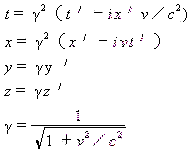三、直线运动中的虚数

　　质点的直线运动对应于数轴上点的谐振动，反映在数值上应是实数的变化，怎么会出现虚数ｉ呢？
　　式（５）已经给出物质运动的空、时、速三者的关系

这就是镜像对称的新概念：ｖ与ｉｖ。

例如：

　　１、伽利略变换

　　相离运动：ｘ′＝ｘ－ｖｔ，
　　相向运动：ｘ′＝ｘ－ｉｖｔ．

    　２、洛仑兹变换

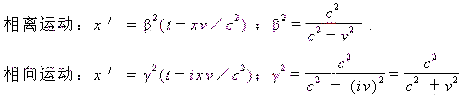
　四、量子力学中的复数

　　量子力学公式中经常出现ｉ，这是什么原因呢？至今所有的教科书中只是使用，没有解释。

　（一）、平面中点的运动是和二维复数对应的

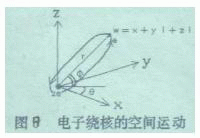
　　电子绕核运动的椭圆轨道是两个互相垂直的谐振动的合成。如图７所示，ｘ和ｙ轴把电子的椭圆轨道四等分。

ｙ轴方向都是关于原点的相离运动和相向运动的对称，属于第二类镜像对称，对称系数都是

    电子在椭圆轨道上不断运动，由ｘ轴正向运动到ｙ轴正向时，方向变化了90°，相当于变化了一个ｉ，再运动到ｘ轴负向，方向又变化了90°，相当于又变化了一个ｉ，但对ｘ轴正向而言方向变化了180°， 属于第一类镜像对称了。

　　为了综合反映出电子绕核运动的这两类不断变化同时存在的对称性，就必须用复数来描述。

　　　　ｗ＝ｘ＋ｙｉ．

或用量子力学公式

（二）、空间中点的运动是和三维复数对应的

　　我们定义三维复数为

　　　　ｗ＝ｘ＋ｙｉ＋ｚｉ．

三维复数的模为

        ｗ1 ＝ｗ2

同一虚轴上的纯虚数可以加、减，即

不同虚轴上的纯虚数不能相加、减，即

于是，电子绕核在三维空间中的运动就可以用三维复数来描述了

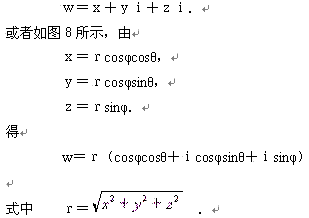　空间任意物体的曲线运动总是由平移和转动合成的，有时相离观察者而去，有时相向观察者而来，为了综合反映运动物体同时存在的两类对称性，用波函数来表示为

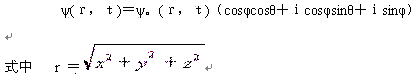
  若用能量、动量以及直角坐标的指数函数表示，则为

  现在我们明白了，原来量子力学公式和洛仑兹变换新公式中的ｉ，只是第二类镜像对称的对称系数。

  例如

  这里存在两类镜像对称：

第一类镜像对称用于相离运动或相向运动的空间反演；第二类镜像对称用于相离运动和相向运动的空间反演。这里请特别注意：“或”与“和”的区别!

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页