物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-经典洛仑兹变换为什么是错误的
![]()
《二十世纪物理学批判》 第一篇 论文二
经典洛仑兹变换为什么是错误的
吴 家 荣
内容提要
本文指出了狭义相对论著作《论动体的电动力学》中存在明显的矛盾。并详细分析了爱因斯坦、洛仑兹、闵可夫斯基和索未菲在推导变换公式时,在哪里出了差错。
关键词: 随意、偷懒、想当然
一、 狭义相对论著作中的矛盾
(一)、同时性概念的矛盾
在运动学部分§1“同时性定义”中有:“按照定义,两钟同步的条件是:tB-tA=tA′-tB(引文一)(《相对论原理》P31,科学出版社,1980)。
在运动学部分§2“长度和时间的相对性”中有这样一段:在运动系统中“根据光速恒定原理,我们得到:
![]()
其中rAB表示在静系统中测得的动杆长度。这样一来,随着动杆一起运动的观察者会发现,这两个钟并不是同步的,而静系统中的观察者则会宣称它们是同步的。” (引文二)(《相对论原理》P36)。
现在我们把上述第一段引文中的公式改写成
![]() (1)
(1)
而把第二段引文中的公式改写
![]() (2)
(2)
这就是说,爱因斯坦同时性定义只适用于“静止”系统,不适用于运动系统。姑且不论“静止”本身也可能是运动的。否则,就不应有两个公式。
但是在运动学部分§3“坐标和时间从静系统到另一个相对它作匀速平移系统的变换理论”中,有这样一段:在从动系统∑'的原点,“令一束光线于时刻![]() 沿X轴向点x'发射,于时刻
沿X轴向点x'发射,于时刻![]() 从该点向坐标原点反射,在时刻
从该点向坐标原点反射,在时刻![]() 到达原点,于是有
到达原点,于是有![]() 或者以函数τ的宗量代入,并应用静系统中的光速恒定原理,就得出:
或者以函数τ的宗量代入,并应用静系统中的光速恒定原理,就得出:
![]()
(引文三) (《相对论原理》P37)。
从上述(引文一)、(引文二)、(引文三)我们看到,爱因斯坦把只适用于静系统的同时性定义运用到动系统中了。因而,爱因斯坦在推导洛仑兹变换公式时是有逻辑混乱的。但若把运动系统当作“静”系统的等价系就可以运用了,但这样一来爱因斯坦的公式(2)又不能成立了。
(二)、爱因斯坦--洛仑兹变换公式和引文四的矛盾
我们先引一段:“我们进一步设想,在杆的两端A与B处各放置一只钟,它们与静系统的钟是同步的,也就是说,在任一瞬时,这两只钟的指针位置都对应于它们碰巧所在之处的‘静系统时间’。所以这两只钟也是‘在静系统中同步’的。” (引文四) (《相对论原理》P35)。
我们先把爱因斯坦推导出的洛仑兹变换公式写下
其中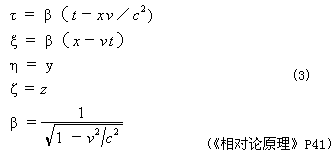
我们再引证一段:“让我们想象有这样一些钟。当它们相对于静系统不动时,能用来指示时间t;而当它们相对于动系统静止时,能用来指示时间τ。设把其中一只钟放在K的坐标原点上,把它调整好,使它指示时间τ。从静系统看来,此钟的快慢如何?
与钟的位置有关的量x,t与τ之间,显然有下列关系:
![]()
所以![]() ”(引文五) (《相对论原理》P42)。
”(引文五) (《相对论原理》P42)。
对比一下这里的公式[由公式(3)推得]和引文四。我们看到这里的τ是动系原点处的时间,t是静系原点处的时间。显然,这里τ是小于t的,爱因斯坦运动钟变慢的结论,就是的根据这个公式得出的。但引文四,爱因斯坦又告诉我们,静系中间各点处的静钟都是同步的;而动系原点处的钟与它所到之处的静钟也是同步的。显然,这里应该是
τ=t (4)
即动系原点处的钟和静系原点处钟是同步的。这才和爱因斯坦的规定(引文四)不矛盾。
如果这个公式(4)成立,则可得出重要结论:
1、按照爱因斯坦同时性定义,这里动钟和静钟的同步是绝对同步。即时间的流逝是绝对的,无论是静系还是动系都是一致的。
2、按照狭义相对论的观点所说的动钟变慢是错误的。运动的钟并没有“真的”变慢,从而运动的杆也没有“真的”变短。
二、科学前辈们在推导洛仑兹变换公式时的差错
(一)、爱因斯坦的随意
现在我们来分析爱因斯坦在推导洛仑兹变换公式(3)时在哪里出现了差错。
本文在引文三中指出爱因斯坦推导洛仑兹变换公式是从逻辑混乱前提下开始的,即把他自己定义的在静系统中适用的公式
![]()
用到了运动系统中,而按照爱因斯坦自己的定义,在动系统中是的
![]()
但是,爱因斯坦从下列前提开始推导还是正确的,因为对于物理规律来说,惯性系是等价的。当得出
![]()
后,写道:“若x′ 取无穷小量,则得出
![]()
或者![]() ”。 (《相对论原理》P37)
”。 (《相对论原理》P37)
对于严格数学意义上来说,任何量值,包括无穷小都是不允许随意处置的。如果x′不是无穷小量怎么办?实际上爱因斯坦是“令x′=x-vt”的,这绝不是一个无穷小量。就说是无穷小量吧,只要不为零,在精确计算中也是不允许省略的,除非取近似值。
爱因斯坦继续推导:“类似地,把刚才的做法应用于Y轴、Z轴,并记住从静系统看来,光沿这些轴的传播速度为![]() ,就得出
,就得出
![]() ”。 (《相对论原理》P38)
”。 (《相对论原理》P38)
这里,爱因斯坦是承认,光在与运动速度V垂直的方向上传播,是受到沿X轴增加方向运动的速度V影响的。所以他让我们记住![]()
爱因斯坦继续写道:
“因为τ是线性函数,就可以从这些方程推出
![]()
其中 a是暂时未知的函数φ(v),为简单起见,假定在K的原点,当t=0时,τ=0。
借助于这些结果,我们不难确定ξ,η,ζ,办法就是用方程表示下列事实:光从运动系统测量起来也是以速度C传播的(这是光速不变原理和相对性原理的共同要求)。对于在时间τ=0向ξ增加方向发射的光线,有
![]()
但是从静系统测量时,光线相对于K的原点是以速度C-V运动的;于是
![]()
根据“光速不变原理”,光从静系统测量时,其速度也应该是C,而不是C-V。C-V的光速是测量不出来的,但C-V的结果可由另外的概念推出。这里我们再次看到爱因斯坦逻辑上的混乱。
爱因斯坦又写道:
“若把这个t代入ξ的方程,则得
![]()
用类似的方法,考虑光沿另外两轴的运动,我们就得出,
当![]()
则有![]()
![]()
于是
以x’的值代入。就得出:
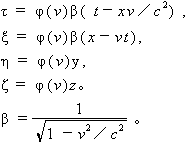
其中:
而φ(v)仍为未知函数。” (《相对论原理》P39)
接着是爱因斯坦证明公式中φ(v)=φ(-v)=1,推导过程都是正确的,我们不再剖析。
这段推导似乎是天衣无缝的。但是,如果我们真的按照爱因斯坦的要求,以x′=x-vt代入,并注意到爱因斯坦是承认,沿X轴方向的运动速度V,对Y轴、Z轴方向光传播是有影响的,就应该得出:
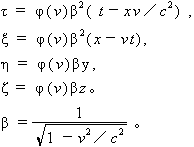
爱因斯坦为什么莫明其妙地要每项省掉一个系数β呢?一方面承认有影响,一方面又硬要把对Y轴、Z轴的影响因子β去掉,不是太随意了吗?
由于爱因斯坦的随意,爱因斯坦推得的经典洛仑兹变换公式显然是错误的。
(二)、洛仑兹的想当然
洛仑兹在提出以自己的名字命名的一组变换公式时,并没有数学推导过程,完全是以假说形式提出的。他在《速度小于光速运动系统中的电磁现象》一文中,于§4“修正的矢量”中,
“令![]() (3)
(3)
![]() (4)
(4)
L为有待确定的另一数量,取
![]() (5)
(5)
(《相对论原理》P10,注意书中公式有误--笔者注)
隔过几行之后,他说:
“至于系数L,应该把它当作是v的函数,当v=0时,L的值为1,对于微小的函数,L与1相差的不过是一个二阶小量。”
洛仑兹在§8“对应状态”中提出了两个正确的假说,但他在§10“地球运动对光学现象的影响”中又否定了。为了避免读者查阅资料的困难,以及阅读本文(“不破不立,边破边立”)的方便,我们将适当增加引用洛仑兹原文,并从中剖析洛仑兹是在哪里出了差错。
洛仑兹说,“现在假定:电子,当它们处于静止状态时我认为是半径为R的球状的,但由于平移的影响,它们的大小就发生了变化,沿着运动方向的长度变小到原来长度的1/βL,与运动垂直方向的长度变小到1/L。” (《相对论原理》P17)
这真是个天才的假设!文中β、L应该是分别代表运动方向和垂直于运动方向的变化系数。如果洛仑兹在以后的推演中不想当然,而是沿着这一天才的假设认真推演下去,他一定能够导出洛仑兹变换正确公式的。
洛仑兹又说,“我们认为,在这种用(1/βL, 1/L, 1/L)表示的变形中,每个体积元里仍然保持原有的电荷。
我们的假定等于说,在一个以速度v运动的静电系统∑中,所有的电子都是扁平椭球,其短轴是沿着运动方向的。如果为了应用§6的定理,令系统作变形(βL,L,L),就重新得到半径为R的球状电子。因而如果用变形(βL,L,L)来改变电子中心在系统∑里的相对位置,又若把保持静止的电子中心置于这样求得的点上,就会得到一个与§6中提到的假想系统∑′完全一样的系统。这系统的力与系统∑的力之间相互关系由式(21)表示。
其次,我们假定,不带电粒子之间的力,以及这种粒子和电子之间的力,当系统平移时所受到的影响,和静电系统中电力所受到的影响完全一样。换句话说,如果就粒子的相对位置而论,系统∑′是由∑经变形(βL,L,L)而得出的,或者说系统∑是由∑′经变形(1/βL,1/L,1/L)而得出的。那么不管组成有质物体的粒子的性质怎样,只要他们之间没有相对运动,就可以用(21)式[系指力的变换形式![]() --笔者注]来描述作用在不作平移运动的系统(∑′)上的力及作位移运动的同一系统(∑)上的力之间关系。
--笔者注]来描述作用在不作平移运动的系统(∑′)上的力及作位移运动的同一系统(∑)上的力之间关系。
由此可见,只要在∑中的一个粒子所受合力为零,则在∑中对应粒子所受合力也一定是零。结果,若忽略分子运动的影响,我们假定固体的每个粒子都在其邻近粒子引力和斥力的作用下处于平衡状态,并认为只存在一种平衡位移,就可以得出下述结论:如果赋予系统∑′以速度v,它就会自行转变为系统∑,换句话说,平移会引起变形(1/βL,1/L,1/L)。”
在§9“电子的动量”最后,洛仑兹写道:“简单地说,用符号∑表示运动系统,∑′表示静止系统,则
![]() (31)”
(31)”
在§10“地球运动对光学现象的影响”中,洛仑兹说:“显然,我们假定在运动系统中存在的状态,的确是可能的” (《相对论原理》P22)
洛仑兹这里指的是运动系统时间的变慢,长度的收缩都是真实的。我认为这种观点是错误的,运动钟运动钟变慢(变快),长度的收缩(伸长),都是由于光速恒定造成我们观察认识事物的相对性而带来的后果。并不是时间真的变慢了,长度真的变短了。
洛仑兹接着写道:
“只要∑和∑′中的电子质量m和加速度a 之积之间的相互关系,和两系统中力的相互关系是一样的,即

这是由式(4)和(5)推出和式子相同的。把它与式(32)结合起来,就可以求出质量之间的关系式:
![]()
把它与式(31)相比较,似乎可以得出:就考虑垂直于平移方向的振动时所要计算的质量而言,不论L值是多少,这个关系式总能成立。因此,必须对L所加的惟一条件是
![]()
基于式(3),则得
![]()
于是我们必须令
![]()
常数值必定是1,因为我们早知道,当V=0时,L=1。(想当然--笔者注。)
这就使我们假定:平移对单个电子和整个有质物体的大小所产生的影响,仅限于运动方向上的尺寸,这影响是使这些尺寸变小到其静止时的1/β。”
这里,我们看到洛仑兹有点想当然,他就没有认真地想一想,当V=0时,这两个系统已经处于相对静止了,还談什么相对论。
至此,洛仑兹把他在§8中我认为是天才的假设给否定了,而得出上述错误的结论。那么差错出在哪里呢?
首先我们回过头来看一下洛仑兹在给出变换假设(3)、(4)、(5)之后写道:
“作为新的独立变量,并用下列公式来定义两个新矢量D’、H‘:
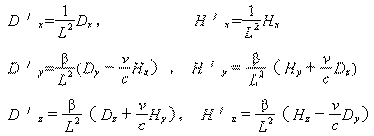
根据式(3)(洛仑兹的天才假设之一。--笔者注),我们也可以把上式写成
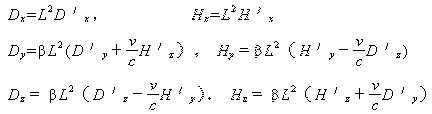
(《相对论原理》P10)
洛仑兹这里的D表示电力矢量,H表示磁力矢量,用的是高斯制。
如果我们用E表示电力矢量,B表示磁力矢量(任何一本电动力学教科书中都有),根据(论文一)《共轭洛仑兹变换》中公式(12)(也就是根据被洛仑兹否定了的天才假设推得),却是
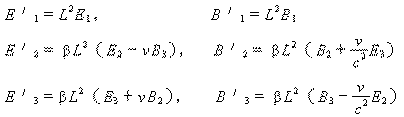
和
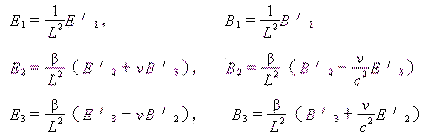
根据这组公式洛仑兹的有质动力F的变换就应该是
![]()
而不是像洛仑兹给出的式(21)那样
![]()
因此洛仑兹给出的?а变换也应该是
![]()
而不是上面引文中公式(32)那样。
这样一来,洛仑兹的质量变换形式就应该是
![]()
而不是像洛仑兹给出的那样
![]()
因而,洛仑兹就得不到L=1(常数)的结论。我们知道:
![]()
这恰恰说明平移不会改变物体的质量,这和质量是标量的概念一致。而通常爱因斯坦相对论的观点在这一点上是矛盾的。
(三)、闵可夫斯基的偷懒
1908年闵可夫斯基在全德自然科学家和医生协会上所作的报告《空间和时间》,对爱因斯坦狭义相对论和洛仑兹收缩从几何角度给予了论证,但他在涉及洛仑兹收缩比率时,仅仅是引用了洛仑兹收缩比率β,并没有给出证明。他写道:
“依照洛仑兹的假说,任何物体在其运动方向上都一定经受一种收缩,事实上,当速度为V时,则按下列比值收缩,
![]()
这个假说令人觉得十分离奇(因为你们搞错了,所以离奇--笔者批注),因为这种收缩不应看作以太或类似东西的阻力所造成的,而应视为天赋的、伴随运动而存在的现象。” (《相对论原理》P66)
闵可夫斯基接着说:“现在我要用我们的图形来表明洛仑兹的假说完全等效于空间时间的新概念,而这些新概念确实使洛仑兹假说更易理解。若为简单起见我们不管Y,Z而设想一个在空间上是一维的世界,那么一条竖直如t轴的平行带,和另一条对t倾斜的平行带(见图1),就分别代表处于静止或匀速运动物体的经
| 历,每个平行带占有一个恒定的空间范围。若OA′平行于第二条带子,我们可以引入t′作为时间坐标,x′作为空间坐标,这样一来,第二个物体就表现为静止,而第一个物体作匀速运动,现在我们假定,设想是处于静止的第一个物体长度为
L,这就是说,第一个带子在 X 轴上的截面等于L·OC,其中OC表示X轴上的单位尺度;另一方面假定设想处于静止的第二个物体具有同样的长度
L,这表示第二条带子的截面Q′Q′的长度(平行于X′轴方向测量)等于L·OC′。现在我们用这两个物体得出同样的洛仑兹电子的象,一个静止,一个作匀速运动。但是,若保持原来的经X,t不变,则对于第二个电子,我们必须用其相应带子的平行于X轴截面作为其大小。由于Q′Q′=L·OC,显然QQ=L·OD′。对于第二条带子来说,若dx/dt等于v,则简单的计算给出 |
 |
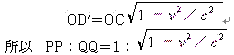 而这就是关于运动着的电子收缩的洛仑兹假说的意义”。
而这就是关于运动着的电子收缩的洛仑兹假说的意义”。
从以上引文我们看到,闵可夫斯基并没有给出“简单的计算”。是偷懒?还是算了,发现与他们原来想象的结果并不一样?
(四)、索未菲的错误
下面我们来看索未菲在给闵可夫斯基《空间和时间》这篇论文所作的注释中是怎样推导的。
“(2)67页21行‘对于第二条带子来说,若dx/dt等于v,则简单的计算给出![]()
在图1中,令α=∠A′OA ,β=∠B′OA′=∠C′OB′,其中最后两个角的相等是由渐近线对新坐标轴(双线共轭径)的对称位置推出的。[1] ([1]是笔者标注)
由于α+β=π/4 ,
sin 2β=cos 2α
在三角形OD′C′中,正弦定律给出
![]()
或者由于OC′=OA′,所以
![]() (1)
(1)
若X,是А′在 X,系统中的坐标,则X · OA和Ct · OC=C t · OA分别是它与坐标轴的相应距离,于是我们有
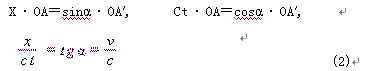
把X与C?的这些值代入双曲线方程中,我们就得出
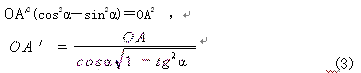
所以,由于(1)和(2)得
![]() (4)
(4)
因为OA=OC,这就是所要证明的公式。 (《相对论原理》P77)
索未菲在上述证明中,有三点明显的错误。
第一,他在图1中以Ct代替闵可夫斯基的t作为一个坐标轴看待了。如引文中[1]指出的地方。
第二,闵可夫斯基在论文中§1“令长度OC′=1,OA′= 1/c ”,(《相对论原理》P63)因而平行四边形OA′B′C′绝非菱形,其对角线OB′是不能平分∠A′OC′的。
即
β=∠B′OA′=∠C′OB′
不能成立。
第三、一般情况下,双叶双曲线的渐近线也不是45度角,因而
![]()
此外,还须提请读者注意,在图1中,A和A′,或B和B′,或C和C′,或D和D′都是同一事件,由图看出四维时空间隔并非不变量。只有当C=∝时,双曲面展为平面,即回到牛顿时空,时空间隔才是不变量。
由于爱因斯坦的随意,洛仑兹的想当然,使他们失去了发现“洛仑兹变换”正确公式的机会,造成二十世纪物理学在相对论领域的神秘和荒谬。
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑