物理科学探疑-网友天空-系统观点--吴家荣--二十世纪物理学批判-共轭洛仑兹变换

《二十世纪物理学批判》第一篇      论文一

共　轭　洛　仑　兹　变　换

吴　家　荣

内容提要：爱因斯坦狭义相对论错误的致命原因是经典洛仑兹变换错误。洛仑兹变换有相互共轭的两种形式，一种形式适用于相离运动，另一种形式适用于相向运动。通过把两种形式的洛仑兹变换代入有关公式直接验证，直观地给出爱因斯坦狭义相对论是错误的。

关键词：　直观给出　　洛仑兹变换　　两种形式

    狭义相对论是建立在洛仑兹变换基础上的。如果洛仑兹变换不是惟一的，（不是通常意义的多种形式，而是本质不同的两组公式）狭义相对论就值得推敲了，我们马上可以写出洛仑兹变换互相共轭的两种形式，经典公式为

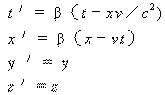(1)

    其中

    这是根据相离运动推导出来的。

    对于相向运动，洛仑兹变换应为下述形式

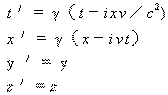(2)

    其中

    上述两个洛仑兹变换公式，对于狭义相对论要说明的一切规律都是等效的。例如，我们可以仿效爱因斯坦的方法验证一下

    球面波在动系∑′中的运动方程为

    现在我们用洛仑兹变换公式(1)变换到静系∑

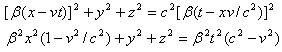
    于是我们得到

    我们再用洛仑兹变换公式(2)变换到静系∑

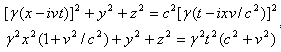
    于是我们同样得到

    这就是说，对于规律，上述洛仑兹变换的两个公式都是正确的。但是对于现象，却会导致不同的结论。例如，相离而去的钟走得慢

    因为

将

    代入

    　爱因斯坦动钟变慢（ t′＜ t ）的结论就是从这里得出的。［1］

    然而，相向而来的钟走得快

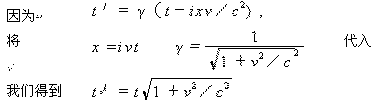
显然有t′＞ t.动钟究竟是变慢还是变快？同理，动杆究竟是收缩还是膨胀？这是一个矛盾。

　　仅仅根据洛仑兹变换的不惟一性，我们就能断定爱因斯坦的狭义相对论是错误的。

　　事实上，洛仑兹变换也不是上述形式。而是适用于相离运动的洛仑兹变换

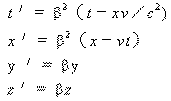(3)

　　适用于相向运动的洛仑兹变换

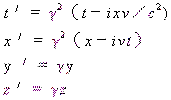(4)

    对于规律，公式(3)、(4)同样正确；对于现象却能导致完美自洽的结论。这些结论，与古今中外千百年来人们的经验常识相符。当本论文集推导出上述“洛仑兹变换新公式”时，那么一百年来，关于“尺缩钟慢”、“时间反演”、“双生子佯谬”等反经验违理性的无休止争论，总算可以掩旗息豉了。
我们仍然仿效爱因斯坦的方法，用洛仑兹变换公式(3)、(4)来验证一下

(一)、 用两种洛仑兹变换公式考察运动学几个问题

１、球面波在动、静两个系统中的变换（电磁场）

    球面波在动系∑′中的运动方程为

    现在用新的变换公式变换

    (1)、用相离运动洛仑兹变换公式(3)变换

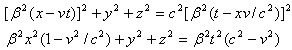
    于是我们得到

    (2)、用相向运动洛仑兹变换公式(4)变换

    于是我们同样得到

２、运动物体的形状在动、静系统中的变化（空间）

    球在动系中的表面方程是

    现在用新的变换公式变换

    (1)、相离而去的球收缩

    因为表面方程不是运动方程，与时间ｔ无关。令ｔ＝０，

则 

    因此，在静止状态下测量为球状的物体，当其与观察者处于相离运动状态时，在静系统看来，就具有扁平椭球的形状，其三轴

    即球在 Ｙ、Ｚ 轴方向上的尺寸也缩短了，缩短的比率是

    而在Ｘ轴方向上的尺寸是按的比率缩短的

(2)、相向而来的球膨胀

或

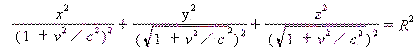
    因此，在静止状态下测量为球状的物体，当其与观察者处于相向运动状态时，在静系统看来，就具有扁平椭球的形状，其三轴为

    即球在 Ｙ、Ｚ轴方向上的尺寸也增大了，增大的比率是

３、运动钟在动、静两系统中的变化（时间）

    (1)、相离而去的动钟和“静钟”比较，绝对一致，相对慢

因为 

将

                                    (5)

　就是说，动钟Ａ与它所到之处的静钟是“同时同步”的，因而也与静系原点处的Ｋ钟是“同时同步”的。这和爱因斯坦的规定：

　　“我们进一步设想，在杆的两端Ａ与Ｂ处各放置一只钟，它们与静系统的钟是同步的，也就是说，在任一瞬时，这两只钟的指针位置都对应于它们碰巧所在之处的‘静系统时间’。所以这两只钟也是‘在静系统中同步’的。”［2］相一致。

　　而爱因斯坦“动钟变慢”的结论是与他自己的规定相矛盾的。
　　对于静系原点处的观察者来说，他“看”到的动钟指示状态应由下式描述：（参见论文四《时空的绝对与相对》公式(4)、(5)）

(6)

    其中：ｔ′为“静系”Σ原点处观察者“看到”的动钟Ａ指示时间．
　　式(5)说明运动钟的绝对时间是不会变化的
　　式(6)说明运动钟的相对时间以(动看静)的比率变慢。

(2)、相向而来的动钟和“静钟”比较，绝对一致，相对快

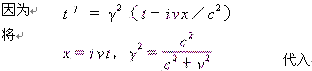
                                 (7)

    当动钟Ａ与观察者相距ｘ相向而来时，观察者“看到”的状态应由下式描述：（参见论文四《时空的绝对与相对》公式(6)、(7)）

    其中　ｘ为计时开始时，动钟Ａ与静钟Ｋ之间的距离。

    式(7)同样说明运动钟的绝对时间是不变的，

    式(8)说明运动钟的相对时间以(动看静) 的比率变快。

    当时，说明相向而来的运动钟离观察者太远(ｘ很大)，以致由动钟发出的光信息还没有到达观察者。

    当时，说明计时开始后，动钟Ａ发出的指示ｔ′＝０的信息，要通过空间一定距离ｘ后才能到达观察者，观察者看到ｔ′＝0的光信息时，他自己的钟Ｋ已经走过了ｔ＝x/c秒。当运动钟到达观察者时，由于动钟Ａ以的比率加快运行，所以到达时，两钟指示一致：

ｔ′＝ｔ.

(二)、我们再考察一个动力学问题

　　在动系统中我们有

                                    (9)

   我们把这个规律用洛仑兹变换新公式，变回到“静”系统。根据相对性原理，在“静”系统中，这个规律仍然具有

    　Ｆ＝ｍａ

的形式。

　１、首先考虑相离运动

(1)、电磁场张量的变换

    我们来考虑电场强度Ｅ和磁感强度Ｂ。设它们在三个坐标轴上的分量分别为(E1、E2 、E3)和(B1、B2、B3)。
　　根据洛仑兹变换新公式，我们有变换矩阵

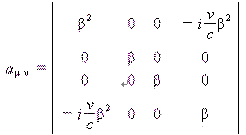(10)

    再利用电磁埸的四维张量公式：［3］

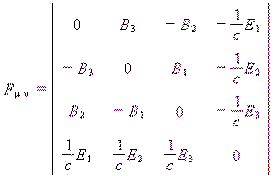(11)

    可得电磁场变换关系

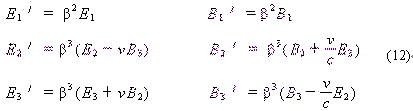
    因为在电场中有质动力为

                                          (13)

    (2)、加速度的变换

　　设带电粒子在静电场中由速度ｖ开始，它相对于动系统Σ′是静止的，在以后的过程中，将获得电场加速，设在动系Σ′中的加速度为

    我们把加速度由动系统变换到“静”系统. 根据适用于相离运动的洛仑兹变换新的公式（３）：

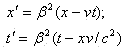
    分别求一阶导数，二阶导数，再运用参数方程的求导公式我们得到

                                 (14)

    将式(13)、(14)代入式(9)得

        Ｆ＝ｍａ

    这里，我们同时证明了

        　ｍ′＝ｍ．

    即质量不会随物体的运动而变化。这和质量是标量，在相互作匀速平移运动的参考系中标量不变是一致的。

    ２、再来考虑相向运动

    同理，我们可以得到

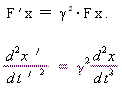
    因而也有

    　通过以上验证，我们看到洛仑兹变换的两个新公式（３）和（４）对狭义相对论要说明的一切规律和现象都是自洽的。而由经典洛仑兹变换演义出来的两个公式（１）和（２）对于狭义相对论要说明的规律和现象却存在着矛盾。可见洛仑兹变换的正确公式应该是（３）和（４）。

［1］《相对论原理》第42页，科学出版社，1980年。
［2］《相对论原理》第35页，科学出版社，1980年。
［3］《电动力学》第249页，郭硕鸿，高等教育出版社，1992年。

版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页