物理科学探疑-网友天空-系统观点-谭星军-开天辟地-论电子结构与原子光谱问题
![]()
开天辟地之一
论电子结构与原子光谱问题
谭星军
Email:txj731@163.com
序
上个世纪初,玻尔理论在解释氢原子光谱问题时获得了巨大的成功,许多人以为解决原子光谱问题指日可待。然而一晃一百多年过去了,众多的有志之士为之不懈奋斗,或心有余而力不足,或是有劲无处使,英雄无用武之地,陷身其中,不能自拔,除了增加了一些晦涩难懂的“理论”、“假设”以外,人们并没有取得突破性的进展。所有的研究成果仅仅只是停留在对已有实验数据的解释上,就连原有的卢瑟福的原子行星模型也被改成一团云雾的“电子云”模型,真是不改还清楚,越改越模糊了。愚以为就人类目前的科技水平而言,要解释原子光谱问题,主要是思维方法问题而不是实验设备问题。这样讲有些人可能会勃然大怒,真是看人挑担不费力,站着说话不腰疼,有本事你试试看!不错,本文的目的就是阐述彻底解决原子光谱问题的方法,既然号称开天辟地,必然有独到的见解,但仅仅有独到的见解还不够,关键是诸位看过以后心服口服,并且立即扔掉以前固执的想法,掌握运用解决原子光谱问题的新观点、新方法,在原子光谱领域干出一番事业来。倘能如此,则足矣。
*1、光子是电子的组成部分
(本节的目的是弄清楚发光现象究竟是由原子的哪一部分来完成的)
燃烧的蜡烛、通电的灯泡、太阳以及宇宙中无数的恒星都能够发光,尽管它们发出的光颜色可能不同;通常我们见到的物体也可以“发光”,只不过这些光属于红外线,肉眼看不见。从广义上来讲,自然界中的一切物质,只要其温度在绝对零度以上,就可以向外辐射电磁波,而人眼能够看到的可见光仅仅是电磁波中的极小一部分。那么,物质是如何发光的?光子是由物质的哪一部分发出的呢?
分子运动论指出,物质是由原子(分子)构成的。在化学变化中,伴随着电子的得失,常常有光子(能量)放出,其它的许多事实也表明,原子是物质中最小的发光单位。既然光子是由原子放出的,那么原子又是如何发光的呢?要弄清这个问题首先必须明白光子是由原子的哪一部分放出的。我们知道,原子是由原子核和核外的电子构成的。在原子发光以前,光子作为一种物质实体,独立于人类的意识而存在,它是不以人们的意识为转移的,那么光子究竟存在于原子中的哪一部分呢?显然,光子或者存在于电子之中,或者存在于原子核中,二者必居其一,而不可能有别的选择。通常情况下,原子核的结合能极大,当原子核裂变以后放出的能量往往在兆电子伏数量级上,而且放出的光子也都是γ射线之类的高能光子,而我们通常所指的发光现象,如可见光、红外线之类的电磁波,其能量都在几个电子伏的数量级上,所以一般的发光现象,都是由原子核外的电子放出光子。我们讨论的焦点也集中在电子发光上。
既然电子可以放出光子,那么在电子发光前光子必然是电子的组成部分,或者说电子有一定的内部结构,光子是其组成部分之一。我们知道,电子带有一个单位的负电荷,而光子却是中性的不带电,这说明电子内部的负电荷不是均匀分布的(因为如果电子内部的负电荷是均匀分布的,那么光子也应该带负电)。我们还不知道电子内部的其它组成部分是什么,但我们可以肯定的是:光子一定是电子的基本组成部分(当然电子内部必然还有带负电荷的其它粒子)。知道上述两点对我们解决原子光谱问题已经足够了。我们从最简单的氢原子入手分析。氢原子是由质子和一个电子组成的。质子带一个单位正电荷,电子带一个单位负电荷,它们之间的距离很小,在纳米的数量级上,所以它们之间的静电力很强。由于电子内部的电荷不是均匀分布的,带负电的粒子在原子核强大的静电引力作用下,必然被吸引向靠近原子核的一方,此时电子产生了形变;如果原子核的静电引力足够强,那么电子就可能发生裂变,作为裂变的产物━━光子就诞生了。电子裂变放出光子以后,其质量变小,体积也相应减小,于是各个部分之间结合得更加紧密,此时电子处于饥饿状态,适当的时候还可能吸收一个光子,这就为电子的下一次裂变放出光子准备了前提条件。而原子主要是通过电子不断地吸收、放出光子来和外界交换能量的。
从前面的分析我们知道,决定电子能否裂变放出光子的因素有两个:原子核的引力和电子内部的凝聚力。这两个力是相互矛盾的,电子就是在这一对相互矛盾的力的作用下处于平衡状态。很显然,原子核的引力总是力图使电子发生形变━━进而产生裂变━━直至放出光子,而电子内部的凝聚力则总是力图使电子凝聚成一个整体━━并尽可能地再吸收一个或多个光子。由于光子有一定的质量,所以电子吸收一个光子后其质量必然增大,放出一个光子后其质量必然减小。可以简单地认为,原子核的引力总使电子质量减小,而电子自身的凝聚力总使其质量增大。正是这一对相互矛盾的作用力平衡的结果导致了电子在原子中能够稳定地存在。那么这两个力对电子裂变放出光子产生什么样的影响呢?首先来看原子核的静电引力。库仑定律指出,两个点电荷的作用力,与它们电量的乘积成正比,与它们之间的距离的平方成反比。
即有![]()
由此可见,原子核对电子的静电引力与原子核自身的电量有关。在原子核与电子距离一定的情况下,原子核电量越大对电子的静电引力也就越大,因而也越容易使电子裂变产生光子;原子核电量越小对电子的静电引力也就越小,因而也不越容易使电子裂变产生光子。对于同一个原子而言,原子核的电量是一定的,原子核与电子之间的静电力仅仅取决于它们之间的距离,距离越小则静电力越大━━因而越容易使电子裂变放出光子。我们再来看电子自身的凝聚力的大小和哪些因素有关。为简单起见,我们仅认为电子是由光子(中性物质)和带负电的粒子组成的。当然这种看法是不完全正确的,但却不影响我们分析问题。在通常情况下,电子内部各部分间存在着排斥力和凝聚力,这两种力处于平衡状态。在原子核强大的静电作用下,电子内部的负电荷有向原子核一面集中的趋势,这个趋势必然引起电子形变,如果原子核的引力足够强则电子就会发生裂变放出光子;反之,如果一个电子裂变放出光子以后,其质量必然减小,此时电子体积减小,其内部结合得更加紧密,这时它可能会吸收一个光子而成为新的电子。在电子和光子相遇后,由于光子不带电,所以当光子进入电子内部以后必然打破了原来电子内部各部分之间的平衡。如果形成的新电子内部各部分之间的凝聚力大于排斥力,则形成的新电子就是稳定的;反之,若形成的新电子内部各部分之间的排斥力大于凝聚力,则形成的新电子就是不稳定的━━它将裂变放出光子。电子和光子从相遇━━结合━━分离需要一定的时间,倘若这个时间极短,那么我们可以认为:电子不与该光子作用;倘若这个时间较长,那么我们可以认为电子吸收了该光子。
以上说了这么多,归结起来就是,光子是电子的组成部分,电子可以吸收一个光子后形成新的、质量更大、内部结合力更弱的电子;也可以放出一个光子后形成新的、质量更小、内部结合力更强的电子。实际上,在上个世纪人们就发现,原子核是由中子和质子组成的,并且也发现了同一种元素的多种同位素。如果有人说同一种元素的原子核(带有相同的质子数)可以吸收几个不同数量的中子形成质量不同的新的原子核(同位素),谁都不会怀疑;但同样是带电粒子,却没有人去分析电子的内部结构,既便有,也没有人把它和原子光谱问题联系起来,实在很可惜。这其中固然有人们思维定势的一面,但最主要的原因还是没法突破解决原子光谱问题的主要屏障━━原子和电子之间的磁力作用。电子的质量可以变化,可以不停地吸收━━放出光子,这是在解决原子问题时我们遇到的第一个屏障━━但不是最主要的屏障,如果您现在还对这个问题持怀疑态度的话,那么下面的几节就不用看了。
**2、电子的质量━━结合能曲线
(本节的中心任务是说明电子质量的可变性)
自然界的规律往往有惊人的相似之处。我们知道,原子核可以裂变,裂变后有能量放出,但只有一些特定质量的原子核的结合能是很大的,人们称之为质量幻数。从微观的角度来看,原子核质量幻数的存在,说明原子核是有一定的内部结构的,也就是说原子核不是一个匀质的硬性小球,它是由比它更低一级的粒子构成的,同时也说明人类目前对原子核内部组成研究的还不是很透彻。和原子核质量幻数相似,电子也存在着质量幻数。即电子的结合力与其质量的关系不是线性的,总有些特定质量的电子的结合力相当大,比其它质量电子的结合力大许多,也就是说,由于电子有一定的内部结构,使得总有一些特定质量的电子是相当稳定的。前面我们指出,电子可以和光子作用,适当的时候可以吸收光子。如果我们能把电子的质量和电子在该质量下电子的结合能描绘出来的话,那么我们将看到一条曲线,这条曲线上的许多峰值也指出电子质量幻数的存在。那么电子的质量━━结合能曲线是怎样的呢?一般说来,电子质量越大则体积也越大,内部各部分结合的越松散,在原子核静电力作用下越容易发生裂变;电子质量越小则体积也越小,内部各部分结合的越紧密,在原子核静电力作用下越不容易发生裂变。也正因为如此,质量越大的电子结合光子的能力就越弱,质量越小的电子结合光子的能力就越强。从光子的角度来看,对不同质量的光子而言,光子质量越小其进入电子内部后对整个电子内部各部分之间的平衡影响也越小,因而和电子的结合力也越大;反之,光子质量越大其进入电子内部后对整个电子内部各部分之间的平衡影响也越大,因而和电子的结合力也越小。
和原子核质量幻数相似,总有特定质量的电子的结合力相当大,比其它质量电子的结合力大许多,这些特定质量的电子往往对应于电子在原子核中的稳定轨道。若以纵坐标表示电子的结合能,以横坐标表示电子的质量,那么电子的质量━━结合能曲线大致呈下降趋势,如图。

注意,在上图中所画的曲线是虚线,这里提醒诸位,千万不能按图对号入座,因为电子实际的质量━━结合能曲线可能与上面所画的有较大的差别。实际的曲线究竟是怎样的,还有待于实验检验。
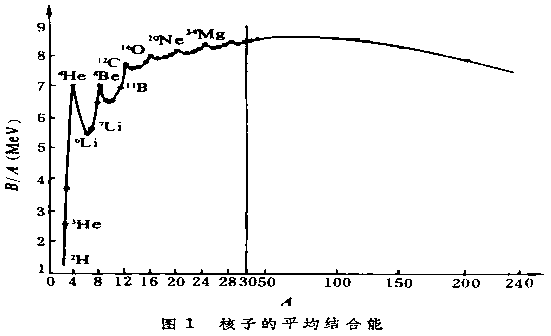
作为对比,我们给出原子核的平均结合能,如上图所示。
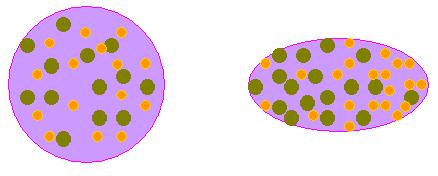
如上图所示,我们用简单的模型来模拟电子受原子核扰动时裂变的情形。在上图中,我们假设电子的内部结构如左图所示,图中金色的圆点代表光子,绿色的圆点代表电子中带负电荷的部分,其余部分我们暂不考虑。在电子没有受到原子核静电引力的时候,光子和带负电荷的部分在电子中均匀分布;当电子受到原子核静电引力作用的时候,由于静电引力的影响,电子中带负电荷的部分向电子的一侧移动,而光子就集中于电子的另一侧,如上图所示。如果原子核的静电引力足够强,电子内部的形变也足够大,此时电子就会发生裂变放出光子。
前面我们指出,促使电子裂变放出光子的力是原子核和电子之间的静电引力,这个力是随着原子核和电子之间的距离减小而迅速增大的。也就是说电子离核越远受到的静电引力越小,电子离核越近受到的静电引力越大。通常情况下,电子带负电,而原子核带正电,在静电力作用下,电子会产生一定的形变(当然原子核也会产生形变,不过由于原子核的结合能比电子的结合能大得多,所以原子核的形变往往可以忽略),如果电子的形变达到一定限度,其内部的凝聚力不足以使电子维持成一个整体,这时电子就会发生裂变,其结果是电子放出光子;放出光子后,电子处于饥饿状态,若原子核的静电引力减小,它就会迅速吸收一个合适的光子形成新的、质量更大的电子,并且这一过程是可逆的。由于静电引力的作用总是使电子裂变质量减小,离核越近电子受到的静电引力越大,电子发生形变放出光子的可能性也越大,所以同一个电子在其处于平衡状态时,离核越近质量越小,离核越远质量越大。这个问题可以从两方面来认识。一方面电子离核越近受到原子核的静电引力越大,必然使其裂变放出光子;另一方面,电子离核越近时只有放出光子减小体积使内部各部分结合得更紧密才能够抵御原子核的静电引力。从一个角度来说,电子离核越近质量越小,其结合光子的能力也越强,或者可以说其饥饿度越大;电子离核越远质量越大,其结合光子的能力也越弱,其饥饿度越小。在多电子原子中,内层电子往往容易吸收能量较高的光子而外层电子往往易吸收能量较低的光子就是这个道理。
通常情况下,电子内部各部分间存在着凝聚力和排斥力两种力的作用,在电子和光子作用以前,电子内部各部分处于平衡状态。在电子和光子作用后,电子内部各部分间的平衡状态被打破━━如果形成的新的电子内部各部分之间的凝聚力大于排斥力,则形成的新的电子就是稳定的;反之,若形成的新的电子内部各部分之间的排斥力大于凝聚力,则形成的新的电子就是不稳定的,将裂变放出光子。显然,电子和光子从结合到分离的过程需要一定的时间,倘若这个时间极短,那么我们可以认为电子不与光子作用,倘若这个时间较长,则可以认为电子吸收了光子。
这里电子质量幻数倒不难理解,关键是电子质量的变化较难理解。从以上的分析可以看出,电子离核越近质量越小,电子离核越远质量越大,当然自由态的电子质量是最大的了。电子吸收━━放出光子这一过程的可逆性就在于,近核轨道上的电子可以吸收一个光子跃迁到离原子核更远的轨道上,也可以放出一个光子到达离核更近的轨道上;而离核较远的轨道上的电子可以放出一个光子到达离核较近的轨道上,也可以吸收一个光子而跃迁到离核更远的轨道上,以上过程可以不断重复下去。在通常情况下,一个原子中的电子吸收━━放出光子的过程不停地重复着,并且一刻也没有停止过。事实上,只要物体的温度在绝对零度以上,电子吸收━━放出光子的过程就一刻也没有停止过,稍后我们会详细讨论,热现象的本质就是原子中电子与外界交换光子(能量)的过程。
*****3、原子核和电子之间的磁力作用
(本节的中心任务是指出原子核和电子不会吸引在一起的原因)
早在几个世纪前,人们就发现用毛皮摩擦过的橡胶棒和用丝绸摩擦过的玻璃棒能够吸引轻小的物体,人们称这种特性为物体带了电。后来人们发现电荷有两种,一种是正电荷,一种是负电荷,比如质子带的就是一个单位正电荷,而电子带一个单位负电荷。库仑定律定量描述了带电点电荷之间静电力的大小,指出两个带电点电荷的作用力在它们的连线上,同种电荷相互排斥,异种电荷相互吸引。(注意,库仑定律并没有指出:仅在静电力作用下,带点点电荷的运动轨迹就一定是直线)。在宏观世界中,库仑定律足够准确了,两个点电荷若不受其它外力作用,仅在静电力的作用下,要么吸引在一起,要么互相分开。其运动轨迹是直线。导致人们产生一个错觉,认为“带电点电荷仅在电场力作用下其运动轨迹是直线”(这个错觉的产生就像人们错误地认为光在空气中总是沿直线传播的一样,实际上“海市蜃楼”等自然现象明显地反映出光在空气中也会沿曲线传播)。这也是大多数人的通病,往往过分相信自己的经验,以至于不能具体情况具体分析。相传李鸿章在第一次吃冰棍时,看见周围冒汽,以为很烫,就用嘴吹,遭到嘲笑。同样的错误我们也会犯。例如,因为宏观点电荷在静电力作用下沿直线运动,我们就固执地认为微观点电荷(包括质子、电子等)在静电力作用下也是沿直线运动的,从而忽视了宏观点电荷和微观点电荷的区别(不知道其他人是否也认为微观点电荷仅在静电力的作用下必将沿直线运动,反正在很长一段时间内我是这样认为的,也走了不少弯路)。事实上,“点电荷仅在静电力的作用下其运动轨迹是直线”这一结论在宏观世界中是足够准确的,但在微观世界中,特别是在原子核和电子这类荷质比非常大的粒子中,我们的经验出了问题,因为原子核和电子这类荷质比非常大的粒子仅在静电力的作用下并不是沿直线运动,而是沿着螺旋线运动的。我个人认为,这是解决原子光谱问题最关键的一步,倘若想通了这一点,那么解决原子光谱问题就容易得多了,所以这一节是整篇文章最难理解、也是人们最不愿意接受的。
库仑定律指出:两个点电荷之间的作用力与它们电量的乘积成正比,与它们之间距离的平方成反比,作用力在两个点电荷的连线上。这就是说,倘若有相距一定距离的两个静止的异种点电荷,仅仅在静电力的作用下这两个点电荷必将吸引在一起,不论这两个点电荷的电量如何,质量怎样变化,这个结果都不会改变。对原子而言,原子核带正电,电子带负电,为什么原子核和电子没有吸引在一起呢?如果认为电子在原子核周围做圆周运动,而原子核对电子的静电引力正好等于电子做圆周运动所需的向心力,所以原子核和电子没有吸引在一起,仅有这样的解释是不够的,也不足以令人信服。我们知道,电子在原子核外做圆周运动时其角动量是不守恒的,先来看一个假设,若一个游离态的电子遇到一个质子,它们必然会形成一个原子。开始的时候,在原子核和电子相距一定的距离而相对静止时,可以认为电子绕原子核作圆周运动的角动量为零,当电子绕原子核周围做圆周运动而处于稳定状态时,其角速度必然不是零,所以在原子核和电子间必然存在着除静电力以外的力。在它们形成原子以前,是什么力给了电子做圆周运动所需的角动量呢?这说明在原子核和电子间并不是仅仅有静电力存在,它们之间一定存在着其它力的作用━━这个力就是原子核和电子之间的磁力。要深刻理解这一点,先来看一个实验。
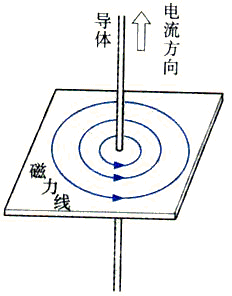
我们知道,当导体中有电流通过时,会在其周围的空间中形成磁场,磁场的方向可以用安培定则来确定。如上图所示。同样,运动着的磁场会在其周围的空间中产生电场,这就是人们常说的电磁感应现象:变化(运动)的电流产生磁场,变化(运动)的磁场产生电场。对于微观原子核和核外的电子来说,它们都处于运动状态,尤其对电子来说,更是处于高速运动状态,其产生的磁场是很强的,那么微观粒子间的作用力如果呢?
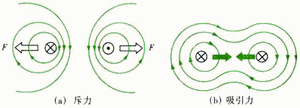
如果给两条平行导线通电,则这两条平行导线形成的磁场会互相影响以相同方向电流的两条平行导线间会产生磁力作用,这个力使它们彼此吸引;反之,若两条平行导线通以不同方向的电流,则它们会相互排斥。如图:

上图所不是不通电时两条平行导线间的受力情况。
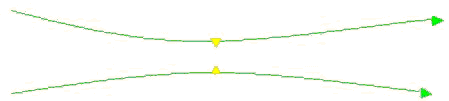
上图是通以相同方向电流时两条平行导线的受力情况。
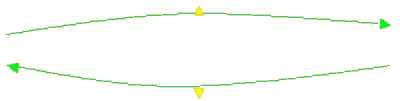
上图则是通以相反方向电流时两条平行导线的受力情况
那么,以上三幅图能说明什么问题呢?
我们知道,通常所说的电流方向是指正电荷的动动方向。就是说,电流方向是正电荷的运动方向,也是负电荷运动的相反方向。换句话说,当正电荷由左向右运动时,电流方向就是从左指向右的,当正电荷由右向左运动时,电流方向就是由右指向左的;但是对于负电荷却恰恰相反:当负电荷由左向右运动时,电流方向是由右指向左的,而当负电荷由右向左运动时,电流方向则是由左指向右的。
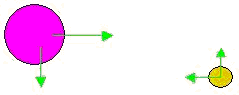
对于两个相向运动的原子核和电子而言,如图,假设左边的是带正电的原子核,右边的是带负电的电子(当然这两者的体积比例可能并不恰当,但这里只是为了说明问题)。

我们知道,当原子核和电子在静电引力作用下相向运动时,原子核向右运动,它所形成的电流方向也是指向右方的;而电子此时向左方运动,它所形成的电流方向则是其运动方向的相反方向,也是指向右方的。这里,我们看到,原子核和电子相向运动时,正相当于通以相同方向的两条平行导线。如图:

此时原子核和电子之间会产生磁力作用,在磁力作用下,它们必将相互吸引,从而引起它们的运动轨迹发生变化。
原子核和电子在静电力作用下将相向运动,此时它们就相当于通以相同方向电流的两条平行导线,在它们之间也将产生磁力作用。静电力的作用总是使电子获得指向原子核的向心速度,而原子核和电子之间的磁力则使电子获得绕核运动的切向速度。我们知道,原子核和电子之间的磁力是随着它们相对速度的增大而增大的。在磁力作用下,原子核和电子并不是沿着直线相互靠近的,而是沿着螺旋线靠近。最终形成稳定的原子系统,如下图所示。
我们知道,静电力的作用使电子获得向心速度,而磁力作用不改变电子运动速度的大小,仅改变电子运动的方向。有了这样的认识,讨论原子问题就容易得多了。我们知道,运动电荷在磁场中受到洛伦兹力的作用,洛伦兹力的方向总是既垂直于电荷速度方向,又垂直于磁场方向,即垂直于磁场方向和速度方向所确定的平面。当带电粒子垂直磁场方向射人磁场时,受到的洛伦兹力方向始终与速度方向垂直,所以洛伦兹力对粒子不做功,它只能改变粒子速度方向而不能改变速度的大小,在粒子只受洛伦兹力的情况下,带电粒子的动能保持不变。洛伦兹力的大小与电荷的电量、运动速度和磁场强度有关,即有:
![]()
式中F为电荷在磁场中受到的作用力,B为磁场强度,![]() 为电荷电量,V为电荷相对磁场的运动速度。对于原子系统而言,原子核和电子的电量都为定值,它们之间的作用力大小仅仅与它们之间的磁场强度和它们之间的相对速度有关。而这个磁场是怎样产生的呢?很显然是由原子核和电子的运动产生的。由于这个磁场也是由由原子核和电子的运动产生的在,故有:
为电荷电量,V为电荷相对磁场的运动速度。对于原子系统而言,原子核和电子的电量都为定值,它们之间的作用力大小仅仅与它们之间的磁场强度和它们之间的相对速度有关。而这个磁场是怎样产生的呢?很显然是由原子核和电子的运动产生的。由于这个磁场也是由由原子核和电子的运动产生的在,故有:
![]()
上式中![]() 1为原子核的电量,E为电子电量,V为由原子核和电子的相对运动速度。把(2)代入(1),有:
1为原子核的电量,E为电子电量,V为由原子核和电子的相对运动速度。把(2)代入(1),有:
![]()
从这里我们可以看出,原子核和电子之间的磁力作用与它们之间的距离有关,它们之间的距离越近,磁力作用就越大。我们可以这样认为,假设有一个电子和一个原子核开始时处于一定的距离并相对静止,此时它们之间的相对速度为零,因此它们之间的磁力作用也是零。此后,在静电引力作用下,原子核和电子开始相向运动,此时由于它们之间的相对速度不是零而开始产生磁力作用,随着原子核和电子之间的距离逐渐缩小,它们的相对速度也逐渐增大,也就是说随着原子核和电子之间的距离逐渐缩小,它们间的磁力作用也越来越大,并且在这个磁力作用下,原子核和电子逐渐偏离了原来的直线相向运动轨道而逐渐变成电子绕原子核做圆周运动。当原子核和电子间的距离足够小,它们的相对速度足够大时,此时磁力作用使电子获得了足够抵御原子核静电引力的绕核角速度,从而形成了稳定的原子系统。
上面我们指出原子核和电子是沿着螺旋线靠近的。现在我们来分析为什么宏观点电荷是沿着直线运动的,以及微观点电荷形成原子系统的临界条件。很显然,要形成微观原子系统的充分条件是点电荷之间的磁力足够强,点电荷的质量要足够小。而点电荷间的磁力是与它们的相对速度有关的,相对速度的获得又是静电力对点电荷做功的结果。至此,我们可以找到它们的关系。
在这一节的讨论中,有一个问题值得我们格外关注。那就是,在微观原子系统中,我们发现,两个电荷之间的作用力随着它们的运动速度的增加会发生变化。也就是说,当两个电荷相对静止时,它们之间只有静电力的作用,而一旦它们相对运动以后,在它们之间就会产生磁力作用。需要我们特别注意的是,这个磁力作用总是在抵消与静电力作用的效果。比如说,原子核和电子之间的静电力作用总是使原子核和电子之间的距离缩小,表现为引力;也而原子核和电子之间的磁力作用总是使原子核和电子相互分离,表现为斥力。也就是说在一定程度上磁力作用抵消了静电力作用的效果。在宏观电荷中,由于电荷的运动速度不是很大,所以磁力对静电力的抵消效果并不明显,而在微观系统中,由于带电粒子的运动速度很大,有的甚至接近光速,所以磁力对静电力的抵消效果将非常明显。明显到什么程度呢?甚至可以明显延长电荷的衰变时间,即产生相对论所说的“钟慢效应”。关于这一点,我们将在第四章中有详细的阐述,这是暂且不提。
上面的分析指出了我们不能用宏观电荷模拟微观原子的根本原因就是二者的荷质比不同,而不是二者的物质波的波长不同。稍后在光的粒子性一文中,我们将详细论述所谓的物质波不过是具有一定内部结构的不同粒子在外力作用下的不同表现而已。我们知道,原子系统在静电引力作用下处于平衡状态时,电子必须有足够的绕核角速度,而正是由于电子和原子核之间的磁力源源不断地为电子提供了绕核角速度,从而维持着原子系统的稳定。电子和原子核之间磁力的产生从根本上来说来源于静电引力,静电引力和磁力从根本上来说其实是一种力的两种不同表现而已。正所谓拔出萝卜带出泥,从原子问题中我们可以看到静电力和磁力有着密不可分的联系,而深入理解静电力和磁力联系是驳斥相对论的的关键所在。有关静电引力和磁力的关系的讨论,超出了本节讨论范围,我们将在驳相对论一文中有详细的阐述。言归正传,下面我们继续讨论原子光谱问题。
4、原子模型
关于原子模型问题,汤姆逊曾提出过原子的蛋糕模型,认为原子中的正电荷象蛋糕一样均匀分布,而电子则象枣一样镶嵌其中,当电子受到外界扰动时会发出特定波长的光子,α粒子散射实验打破了这一模型。后来卢瑟福提出原子的行星模型,认为原子世纪就象太阳系一样,处于核心位置的原子核(太阳)靠其强大的静电引力使电子围绕它旋转,人们认为电子绕核旋转这一过程是电荷做加速运动的过程,必然会放出电磁波,随着电子能量的减小,电子将沿着螺旋线落入原子核中,事实上原子系统是相当稳定的。原子的行星模型再次遭到了否定。再后来,有人提出了原子的电子云模型,指出在某一瞬间,不可能准确测定出电子在原子中的具体位置,这就是有名的测不准关系了。事实上,物质波理论把微观原子世界神秘化了,电子并非人们想象中的一团云雾,在某一瞬间我们可以准确地描绘出电子在原子中的位置。

上图就是汤姆逊提出的原子(蛋糕)模型,他认为电子在原子中按一定的几何形状排列,当电子偏离平衡位置产生振动时,就会发出一定频率的光子。
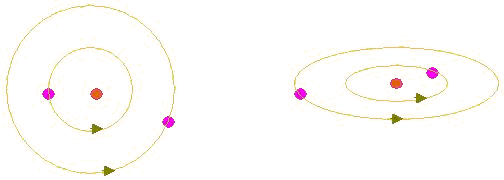
上图是卢瑟福提出原子(行星)模型,他认为原子核就象太阳一样处于原子系统的中位置,而电子则象太阳系中的行星一样绕原子核做圆周运动(尽管我画的不是很圆,但差不多就是这样的)。在卢瑟福原子(行星)模型的基础上,后来又有人提出原子中电子的运动轨道不是正圆,而是椭圆,如上图所示,他们甚至为此模型构筑了大量的公式,不过作用不大。不管怎样,原子模型是正圆也好,椭圆也好,两种观点大体上是一致的。
上图就是原子的“电子云”模型,持这种观点的人认为电子就象云雾一样笼罩着原子核,在某一瞬间,不可能准确描绘出电子在原子中的确切位置,这就是后来的测不准关系的依据之一。因为这种解释是比较模糊的,只有智商极高的人才能理解,所以我对电子云模型一直也搞不清楚,我不知道在分析原子光谱现象中,人们为什么丢掉了可以有效描述原子核和电子之间作用力的库仑定律?当然,我画的图中电子的个数是可以数出来的,并不象云雾,但大体上就是这么个意思,如果有功夫的话,倒可以多画几个电子。但不管怎样,画得再多意义也不大。
我们认为,电子在原子中的运动轨迹是可以描述的。即在某一瞬间它有一个确定的位置,只要知道了电子的受力情况,就可以计算出下一瞬间电子在原子中的位置(注意,这里我们说可以准确描述电子在原子核中的情况,指的是只要我们想这么做,我们就可以做到,而没有其它不确定的因素在里面,打个最简单的比方,就象只要我们吃饭必然就可以饱肚子一样)。换句话说,上帝不玩掷骰子游戏,所有的不确定因素都是我们对事物的本质认识不足造成的,世界是可以认识的,任何不确定的因素都将随着人类认识的深入而逐渐明朗。通常情况下,由于电子时刻不停地受到光子的扰动,不断地吸收各种能量的光子,也不停地放出各种能量的光子,所以可以肯定电子在原子核中并不是处于稳定状态,因而它的运动轨迹也不是正圆。一般来说,温度越高,电子受到扰动的机会和它受到的扰动力就越大,其运动轨迹偏离圆形的趋势越明显,但原子核和电子之间的磁力总是试图把电子拉回圆形轨道;温度越低,电子受到的扰动越小,电子的运动轨迹越接近圆(只有在绝对零度并且电子不受到外界扰动时,电子的运动轨迹才可能是正圆)。从这个意义上来说,原子模型可以看作是卢瑟福的行星模型和电子云模型的结合:温度越低,原子模型越接近行星模型;温度越高,原子模型越接近电子云模型(但在某一瞬间,电子在原子核中有确切的位置)。或者说,当我们把卢瑟福的行星模型从二维平面拓展到三维空间时,就比较接近原子系统的真实情况了。

上图是我所画的常温下的原子模型,原子核处于原子中心位置,电子距原子核的远近是可以变化的,即电子离核的距离有一个最大值和一个最小值,通常情况下,当电子受到外界扰动时,电子在以原子核为中心、以最大值为外界、以最小值为内界的圆环内运动,当然这是从二维平面空间来观察的。实际上,在真实的三维空间中,电子的运动区域是以最大值为外部边界、以最小值为内部边界的球壳内。但电子在某一瞬间有确定的位置。假设我们有一架摄影机,可以用来给原子摄影,我们会发现,在某一时刻,电子受到一个指向核外的扰动(这个扰动通常是电子与光子作用),它会从离核较近的地方运动到离核较远的地方,但在原子核的磁力作用下,过一会儿,电子又会回到离核较近的地方。要注意的是,此时电子的运动不是我们所说的轨道跃迁,而这一过程是频繁发生的。电子发生轨道跃迁的充分必要条件是电子吸收了一个指向核外的光子,受到指向核外的扰动,并且这个光子的质量为特定质量,电子吸收了这个光子后,形成的新的电子内部的结合力很大。通常情况下,电子发生跃迁的机率很小,也许是百万分之一,也许是千万分之一,甚至没有这么大的机率,但因为电子与光子之间的相互作用是非常频繁的,也许每秒钟上百万次甚至上千万次,所以在一定条件下电子也能够发生跃迁。
当物体的温度在绝对零度时,可以认为在单电子原子(如氢原子)中电子的轨道接近正圆(因为此时电子基本上不受外界扰动)。而在常温下,电子的运动轨迹接近电子云模型。这里我们所说的电子云是指电子以某一平衡位置为中心活动。举个例子来说,处于基态的氢原子中电子轨道为0.53纳米,那么电子可能的活动范围就是0.53±X纳米,当电子受到离核扰动时,它运动到离核0.53+X纳米处,而当电子受到指向原子核的扰动时,它运动到离核0.53-X纳米处。在某一瞬间,电子在原子核中有确切的位置,但假如我们有一台特殊的照相机,可以给电子照相,当我们把许多照片重叠在一起时,我们会发现电子有一定的活动范围,即0.53±X纳米。而电子的活动范围随温度升高而增大,温度越高电子越活跃,其活动范围也越大。需要强调指出的是,在通常情况下,电子总是处于不稳定状态,也就是说,总有光子对电子进行扰动,这个扰动有指向原子核的也有远离原子核的,所以电子离原子核也是时远时近的,受其影响,电子的电势能也是时大时小,速度也在不断发生变化。
从另一角度来看,热胀冷缩现象对于原子同样适用。温度越低电子离核越近,温度越高则电子离核越远,表现在原子的体积上也有变化,温度越高,电子离核越远,倘若把电子到达离原子核的最远距离作为原子半径的话,那么相应地原子的体积也越大;温度越低,电子离核越近,相应地原子的体积也越小。这也导致了电子得失的难易程度发生很大的变化。温度越高电子离核越远,受原子核的束缚越弱,所以越容易失去;温度越低电子离核越近,受原子核的束缚越强,所以越不容易失去。这一点在化学变化中很容易得到验证,化学反应的速度与温度关系极大,温度越高化学反应就越容易进行,反应速度也越快;温度越低化学反应就越不容易进行,反应速度也越慢。我们从微观角度来看,温度越高,对于参加化学反应的各种原子来说,它们的最外层电子离核距离更远,所以更容易失去。
5、稳定轨道的形成
在任何人试图研究原子光谱问题以前,原子系统的稳定性是首先要搞清楚的问题,只有解释了原子系统的稳定性,才有资格分析原子光谱问题,如果连原子系统的稳定性问题都没有解决,那么其构建的原子模型肯定是错误的,也更谈不上研究原子光谱问题了。卢瑟福的行星模型在一定程度上反映了原子系统的真实性(这个问题在后面有专门的阐述),但人们普遍认为,在卢瑟福的原子行星模型中,因电子绕原子核运动时存在的加速度而不断向外辐射能量,从而电子的运动速度越来越小,最终导致原子中正负电荷吸引到一起,因而卢瑟福的原子行星模型是不稳定的,但实际上原子是非常稳定的。以前我也认为电子绕核运动会向外辐射电磁波,随着电子能量的减少,电子最终将沿着螺旋线落入原子核,即使电子不落入原子核中,最好的情况下,假设电子不向外辐射电磁波,那么在光子的扰动下,比如电子受到一个指向原子核的扰动,它就获得了指向原子核的速度,也会导致原子核和电子吸引在一起,原子也要分崩离析,可是事实上原子是相当稳定的(即便是现代有名的电子云模型,其实也远远没有解决原子系统的稳定问题,这里暂且不去讨论)。还有,原子系统的稳定性是不是暂时的,比如说原子系统存在最长寿命什么的,但这种情况又不太可能,那么,原子的稳定性是怎样形成的呢?
通常情况下原子是非常稳定的,我们认为原子系统的稳定性主要表现在以下几个方面:第一,带正电的原子核和带负电的电子在静电力作用下不会吸引在一起,而是形成电子绕原子核旋转的稳定的原子系统;第二,不管电子受到指向原子核的还是远离原子核的扰动,通常都能够回到原来的位置(这个位置相当于重力场中的势能最低点,也好象弹簧受力后总要回到平衡位置一样),而不论这个扰动的发生是多么频繁;第三,把原子加强热使之成为等离子体(自由电子和原子核的混合体),冷却后依然能够形成稳定的原子系统,而且原子的分解、结合的过程可以重复无限次,换句话说,如果我们左手拿一个电子,右手拿一个原子核(这当然不可能),要想把它硬挤在一起也是不可能的,就好像不用外力让两个磁铁的同极吸引在一起一样做不到;第四,原子系统能够稳定存在几十亿年甚至上百亿年,并且没有证据表明几百亿年之后原子系统就会分崩离析。我曾经多次想过,研究原子系统稳定存在的寿命,比如几十亿年或上百亿年什么的,但到头来发现原子系统可以稳定的、无限期的存在下去。事实上,作为物质存在的一种方式,原子系统是相当稳定的;同时原子系统也是相当活跃的,原子中的电子时刻不停地与外界交换着能量━━光子,也正因为原子中的电子能够经受住光子对其时刻不停的扰动,所以原子系统是很稳定的。下面我们就来分析原子系统能够稳定存在的原因。
(一)关于原子系统稳定存在的原因,我们认为也要从以上几个方面分析。在前面的第三节中,我们初步讨论了带正电的原子核和带负电的电子在静电力作用下形成电子绕原子核旋转的稳定的原子系统的原因。下面我们来分析原子中的电子受到指向原子核的扰动时原子稳定存在的原因。
假设在某一瞬间电子在原子中处于稳定状态时的质量为m,原子核的质量为M,电子与原子核相距R,电子绕核速度为V,因为此时电子在原子核中处于稳定状态,则电子与原子核之间的静电力恰好提供了电子绕核运动所需的向心力,即有:
若此时电子受到一个指向原子核的质量为m1的光子的扰动,则在电子与光子结合的一瞬间电子的质量变为(m+m1),这个新的质量为(m+m1)的电子将在惯性的作用下向原子核运动,所以电子与原子核之间的距离也将由原来的R减小,假设电子与原子核之间的最小距离为R-r,由前面的分析我们知道,随着电子与原子核距离的减小,原子核对电子的静电引力迅速增大,这个迅速增大的静电引力必将引起电子的变形。而当电子与原子核之间的距离最小时,原子核对电子的静电引力最大,如果此时质量为(m+m1)的电子的内部结合力不足以抵御原子核的静电引力作用,那么这个质量为(m+m1)的电子将裂变放出光子重新形成稳定的电子。
这里有一点要强调的是,裂变后的电子必然是非常稳定的并且其内部结合力足以抵御原子核的静电引力作用(不然的话它还会继续裂变)。根据电子质量结合能曲线我们知道,在质量为(m-m1)~(m+m1)范围内的电子,只有质量为m的电子的结合力是最大的,所以裂变的产物只可能是质量为m的电子和质量为m1的光子。也就是说,在某一质量范围内,电子的裂变方式是唯一的(因为电子在一定的质量范围内结合能最大值只有一个),这实际上也就指出了电子的轨道不不连续性的实质。这里我们再次用到了电子的质量—结合能曲线表,表中峰值部分表示电子结合能的极大值,而在峰值部分两侧,电子的结合能迅速减小。这充分说明电子是有一定的内部结构的,可惜的是,以我们目前的科技水平,我们还不能够观测到电子的内部结构,否则的话,我们的理论将不再是建立在空中楼之上。那么,我们是如何得出电子的质量—结合能曲线存在峰值的结论的呢?坦率地说,一方面我们参照了原子核的质量—结合能曲线,另一方面就是我们的推理了。至于这个推理正确与否,则有待于实验检验了。
(二)接下来我们来讨论原子中的电子受到远离原子核的扰动时原子稳定存在的原因。
同样,我们假设在某一瞬间电子在原子中处于稳定状态时的质量为m,原子核的质量为M,电子与原子核相距R,电子绕核速度为V,因为此时电子在原子核中处于稳定状态,则电子与原子核之间的静电力恰好提供了电子绕核运动所需的向心力,即有:
若此时电子受到一个远离原子核的质量为m1的光子的扰动,则在电子与光子结合的一瞬间电子的质量变为(m+m1),这个新的质量为(m+m1)的电子将在惯性的作用下远离原子核运动。我们知道,电子远离原子核运动时要克服静电引力,所以电子的速度也越来越小。随着电子离核越来越远,它克服静电引力所做的功也越来越多,电子的速度最终会减小到零。事实上,在电子的速度没有减小到零以前电子就在原子核静电引力的作用下又被重新拉向原子核了。设电子与原子核之间的最远距离为R+r,则此时电子的速度最小,此后在原子核静电引力作用下,电子开始向原子核运动。当电子越过平衡位置(即电子与原子核相距R的位置)以后,电子将在惯性作用下继续向原子核靠近并到达距核R-r的位置,此时电子在原子核强大的静电引力作用下必然会裂变放出质量为m1的光子重新成为质量为M的电子。接下来电子回到平衡位置的情形前面讨论中已经谈到了。
上面我们讨论的只是两种极限情况,并且是在平面内讨论的,实际上电子受到光子的扰动是在三维空间中进行的,情况要复杂得多,但都不超出上面讨论的极限情况。
我们认为,电子在原子核中处于稳定状态时,它的轨迹是圆。因为当电子的轨迹不是圆时,它总要受到磁力的作用,这个力使电子的切向速度增加、运动轨迹向圆靠近。而电子受磁力作用时它的运动轨迹就要发生变化,就不是稳定的,只有当电子的轨迹是圆时才不受磁力的作用,所以说电子在原子核中的稳定轨迹是圆。太阳系中的行星在太阳引力作用下,其运动轨迹可以是圆或椭圆,但在原子系统中,电子在原子核静电力和磁力的共同作用下,其稳定轨迹只可能是圆而不可能是椭圆。
6、热现象的本质
什么是热现象?这似乎是不是问题的问题。人们通常认为,热现象是大量分子无规则运动的反映,温度越高分子的平均速率越大,温度越低分子的平均速率越小。果真如此吗?我们知道,太阳时刻不停地向外抛射高能粒子,宇宙中其它恒星也在不停地向外抛射高能粒子,这些高能粒子的速度甚至接近光速,并且可以认为这些粒子的运动是杂乱无章的(因为粒子抛射源不同),按照分子运动论的解释,宇宙空间的温度应该是很高的,至少比恒星内部还要高;无论向哪个方向看去,宇宙空间也应该是很明亮的。但事实上宇宙空间是漆黑的一团,温度只超过绝对零度一点点。这些现象该怎样解释呢?难道只有在地球上分子的杂乱无章的运动才是热现象而宇宙空间中粒子的无规则运动就不是热现象吗?很显然,分子运动论解释不了上述事实,这说明其本身存在着缺陷。宇宙中有许多高能粒子在做杂乱无章的运动,而且速度很高,但宇宙空间的温度又很低的事实说明粒子运动速度大未必温度就很高,物体的温度不是由组成它的原子(或分子)的平均运动速度决定的。温度升高,原子(或分子)的运动速度增大,但反过来,原子(或分子)的平均速度增大并不意味着温度升高。温度升高只是原子(或分子)平均运动速度增大的充分条件,但不是必要条件。再者,分子运动论对单个的原子(或分子)没有定义温度的概念,因为他们认为热现象是大量分子无规则运动的反映,讨论单独的原子(或分子)的温度是没有意义的。从分子运动论的角度来讲,单个分子运动速度的大小没有意义,也就是说分子运动论没有对单个分子定义热的概念,然而实际上,对于单个的原子、分子而言,他们也有温度,也可以定义热及温度的概念。想一想热现象从最初的热质说发展到分子运动论,人类的认识的确是有了很大的进步,但分子运动论毕竟是在人们对原子结构认识不深的情况下提出的,在人类已经开始深入研究原子光谱问题的今天,仍然把热现象仅仅理解为分子的运动,未免有点五十步笑百步了。热现象本质是什么?我们认为它是微观世界能量传递过程的一种表现,只要有能量传递,就有热现象。单独一个分子、原子,如果它向其它分子、原子传递能量,这时就产生了热现象,那么我们就可以给这个分子、原子定义温度。换个角度来看,既然由大量原子、分子组成的物质可以有温度,为什么单个的原子、分子就没有温度呢?给原子、分子定义温度有没有实际意义呢?如果有意义,单个原子、分子的温度该如何定义呢?
在化学变化中,温度对化学反应速度的影响十分明显,温度越高化学反应速度就越快。分子运动论对上述现象的解释是乏力的、难以令人信服的。分子运动论认为,热现象是大量分子(原子)无规则运动的反映,温度越高分子的平均速度越大,温度越低分子的平均速度越小,在通常情况下,大量分子中有的运动速度大,有的运动速度小,但大致服从泊松分布,即大部分分子的运动速度都在一定的平均范围内,速度特别大和速度特别小的分子数量都很少。根据分子运动论对化学反应的解释,温度升高,分子的平均运动速度增大所以化学反应速度加快。但事实上,化学反应速度几乎与分子的运动速度无关(例如对于气体和气体、液体和液体之间的反应速度)。在通常情况下,化学反应常常伴有能量的转移(如发光、发热),分子运动论对此无法解释。谁也不会否认,发生化学变化的标志就是分子或原子间产生了电子得失或偏移。那么很自然,影响化学反应速度的直接原因就是电子得失的难易程度。在人们已经深入了解了原子结构及电子不同跃迁轨道的今天,说速度快的分子中的电子容易失去而速度慢的分子中的电子不容易失去,难免贻笑大方了。而分子运动论的直接推理结果就是原子中电子得失的难易程度与整个原子的运动速度有关。稍微有一点物理学常识的人都知道,在一个原子中电子得失的难易程度与原子本身的速度无关,要想从一个原子中电离一个电子,必须给这个电子增加一定的能量,而电子电离能的大小仅仅取决于该电子距核远近,电子离核越近需要的电离能越大,电子离核越远所需的电离能越小。我想不再需要更多的理由(如果需要的话,还可以举出上百个理由),也该到了修改热现象与分子运动论的时候了。分子运动论无疑在历史上起过积极的作用,但随着人类认识的进一步深入也该补充新的内容了。
我们知道,原子是由原子核和电子组成的,通常情况下原子和光子的作用主要是电子和光子的作用,原子和外界能量交换主要体现在电子的质量变化上,电子离核越近质量越小,相对应的温度也越低;电子离核越远质量越大,相对应的温度也越高。而电子离核越远必然越不稳定,其储存的能量也越多,电子离核越近越稳定因而其储存的能量也越少。在原子系统中虽然是电子储存能量,但离开了原子核电子的能量就无从体现,所以从这个意义上来说,可以把原子看作储存热量的最小单位,单个原子也有温度,因为它可以储存热能。但单个的带电粒子如质子、电子在不受外界任何扰动时,即便速度再大也不会向外界释放能量,因此它们都不能储存热能,因而其也没有温度,或者说对于单独的带电粒子而言,温度对于它们是没有意义的。但有一点是特例,如果单个的原子核或其它粒子是不稳定的,也就是说如果它会发生衰变,那么它就会向外界释放能量,这时它也有温度。从理论上讲,万有引力、电磁力等场力的产生,是物质不断与外界交换能量形成的,一旦物质与外界交换能量的过程不存在,力场也将发生变化并将逐渐消失。所以任何物质都有温度,因为任何物质都不可能单独存在,它总要与其周围的物质交换能量。对宏观物质而言,它们可以通过对流、辐射、热传导等多种方式与外界交换热量,对单独的原子而言,绝大多数情况下它主要是通过电子与外界交换能量。
应该看到,原子(分子)的高速运动所具有的能量仅仅是原子(分子)的动能而不是原子(分子)的热能,和宏观物体一样,原子(分子)速度大未必温度高。宏观物体的速度与其温度无关,原子(分子)也是如此。一个原子(分子)的速度比其它原子(分子)的速度大,只能说明它的动能大,储存的热能未必就多。热能仅储存于原子核和电子形成的原子体系中,两者中缺少任何一个都不能储存热能。而且原子(分子)的热能绝大部分都储存在电子中,因为原子核是非常稳定的,通常情况下它不会吸收放出光子--质量也不会发生变化;而原子中的电子就不同了,它的质量时刻在变化着,因为它不停地与光子作用,总在不断地吸收--放出光子,不断地与外界交换着能量,可以说,原子与外界交换能量的过程主要是靠电子完成的。
今后也许在相当长的一段时间内,我们都不可能直接观测到电子质量的变化,也就是说我们在相当长的时间内都不能直接观测到原子质量的变化,但我们可以明确地指出,对于同一种原子而言,热现象和原子质量的关系非常明显,原子质量越大对应的温度越高,原子质量越小对应的温度越低。我们认为,对于原子的温度,最好的衡量标准就是它的质量而不是原子的运动速度。应该指出的是,对于一个原子而言,其质量是时刻变化的,所以原子的温度也是处于时刻不停的变化之中。而我们通常所说的物质的温度则是大量原子的平均温度。
7、原子光谱
长期以来,一个问题一直困扰着我,那就是为什么物质的发射光谱是连续光谱,而单个的原子其发射光谱是明线光谱呢?我们知道,太阳能够发出连续的光,仅在可见光波段就有红、橙、黄、纪、绿、蓝、靛、紫等七种颜色,燃烧的蜡烛、点亮的电灯也能够发出一定范围内连续的光,为什么单个的原子(或分子)其发射光谱就不连续了,成为明线光谱了呢?难道物质发光不是单个原子(或分子)发光的累积吗?如果是的话,则物质的发射光谱也应该是明线光谱,但事实上物质的发射光谱是连续光谱。对以上问题,当代物理学并没有给出答案,即便是有,也是很含混的,解释不清楚问题的实质。
在解释原子光谱问题时,首先应该明确,原子(分子)是物质发光的最基本单位,而电子则是发光的最基本粒子,就我们目前所指的发光现象而言,绝大部分是由电子来完成的。因为原子是由原子核和电子组成的,原子发光只能是由其组成部分发出光子,即或者是原子核放出光子或者是电子放出光子再或者是二者同时放出光子,三者必居其一,而不可能有别的选择。原子作为发光的最基本单位,常常被人误解为原子本身就能发光。这实际上是对原子结构认识不清楚造成的。如果原子作为一个整体发光,那么原子内部的结构是怎样的,是汤姆逊的蛋糕模型吗?显然这不是的。若认为原子发光是原子核发光,我们知道,原子核的结合力是很大的,它通常在发生变化时放出γ射线,γ射线属于高能光子,并不是我们通常意义上所讲的原子发光现象涉及的低能量的光子。所以原子发光实际上就是电子发光。
既然原子是物质发光的最基本单位,而电子则是发光的最基本粒子,所以既然物质的发射光谱是连续光谱,那么原子的发射光谱也应该是连续光谱,也就是说既然原子的发射光谱是连续光谱,那么电子就能够发出连续波长(任意能量)的光子,显然这与我们观测到的原子的吸收光谱是暗线光谱而原子的发射光谱是明线光谱的实验现象不符合,但却是千真万确的事实,稍后我们会对此作出解释。这种提法不是为了标新立异,哗众取宠,这是我们在深刻认识原子结构上提出的符合事物本来面貌的观点,也是在实践过程中的经验总结。事实上,我们把原子的吸收光谱和明线光谱单独作为一节来阐述,就是为了深刻分析原子光谱问题。
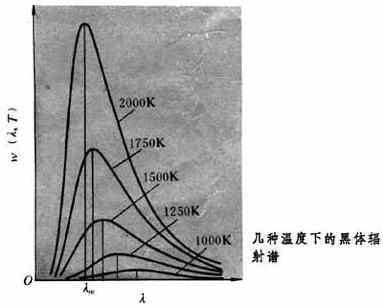
言归正传,我们现在来探讨为什么原子的吸收光谱是暗线光谱。这个问题实际上可以划分成两个问题,一是什么样的电子可以吸收光子?二是满足什么条件的光子容易被原子吸收?前面我们分析指出,被原子核束缚的电子是处于饥饿状态的,它们都可以吸收光子。这样看来,什么样的光子都可以被电子吸收。其实不然,因为电子在原子中时刻受到原子核的静电引力作用。如果电子吸收了一个质量为m的光子,而电子和该光子的凝聚力又小于原子核对电子的静电引力的话,那么重新生成的电子就是不稳定的,必将放出这个光子。根据电子的质量--结合能曲线我们知道,而只有恰当质量的光子和电子结合后凝聚力才是很大的,可以抵御原子核静电引力的作用,这样的光子才能被电子吸收。举例来说,设电子的质量为1000000,光子的质量可以从1到10000连续变化,而电子结合能极大值对应的几个质量分别是1000050,10000100,1000300,10000500等,并且假设开始时电子处于离核最近的轨道上,其质量为1000000,若此时有自然光--质量(能量)连续变化的光子(其质量从到1到1000连续变化)照射到原子上,那么电子最可能吸收哪些质量的光子呢?显然是质量为50、100、300、500的光子。因为电子和这些光子结合后电子的质量分别是1000050,10000100,1000300,10000500,而电子的这些质量最稳定。所以若质量从1到1000的连续光经过原子后,连续光谱中会出现几条暗线,这些暗线对应的光子质量为50、100、300、500,因为电子对这些光子的吸收率要比其它质量光子的吸收率高许多倍。
接下来我们来看电子的轨道跃迁情况。假设电子质量为1000000个最小光子的质量数量级,电子的结合能极大的质量分别是1000050,10000100,1000300,10000500等,当一束光经过原子时(假设光子质量从1到1000连续变化),对于处于近核轨道上质量为1000000的电子而言,它只会吸收质量为50、100、300、500的光子,对于其它质量的光子,电子基本上不会吸收。为什么原子中的电子会吸收质量为50、100、300、500的光子呢?这是因为处于近核轨道上的电子质量为1000000,而与其质量接近结合能又大的电子的质量分别是1000050,10000100,1000300,10000500等,而当电子吸收了质量为50、100、300、500的光子后,形成的新电子内部结合能较大,因而较稳定能在离核较远的轨道上存在较长的时间,所以这些光子较易被原子吸收。那么原子中电子为什么又会吸收质量为200、250、450的光子呢?我们可以这样考虑,当处于近核轨道上质量为1000000的电子吸收了一个质量为50的光子后,它会跃迁到离核稍远的轨道上,此时形成的电子质量为1000050,而若它吸收一个质量为250的光子就可能再形成质量为1000300的较稳定的新电子。这样,质量为1000050的电子可以吸收质量为250、450的光子。同样质量为1000100的电子可以吸收质量为200的光子。
但我们也应该明确看到,电子对不同质量的光子的吸收率是不同的。这是因为在一群原子处于基态时,绝大部分是处于基态的,基态的电子对质量为50、100、300、500的光子吸收能力强,而质量为1000050,10000100,1000300,10000500电子则是由基态(质量为1000000的)电子吸收光子后产生的,其数量必然远远小于处于基态的电子的数量,所以这一部分电子吸收的质量为200、250、450的光子数目也必然较少。打个不恰当的比方,假设处于基态的电子数目有1万个,而这1万个电子在同一时间有1000个电子吸收光子,由前面所述我们知道对于质量为1000000的光子而言,若它对四种质量的光子吸收机率相同,则在同一时间内,这1000个电子有四种吸收光子的选择,其吸收质量为50、100、300、500的光子各有250个。现在来看吸收了50个光子后质量为1000050的光子,它仍然可以吸收质量为50、250、450的光子,即有三种选择,若其对上述光子的吸收能力相同,则在同一时间内吸收质量为50、250、450的光子的电子数目都是83个。那么很显然,对于质量从1到1000连续变化的光子来说,经过10000个原子吸收后,有250个电子吸收了质量为50、100、300、500的光子,有83个电子吸收了质量为50、250、450的光子,所以形成的暗线的明亮程度也不一样,质量为50的光子对应的暗线最暗,而质量为250、450的光子对应的暗线最亮。而大多数光子基本不被电子吸收,或者吸收后在极短的时间内又放出,所以只有特定质量的光子被吸收得多,形成吸收光谱中的暗线。
观察原子吸收光谱和明线光谱的不同之处在于,吸收光谱中的暗线是在明亮的背景中形成的,即使电子也吸收了某一质量的光子,但由于吸收的非常少,造成谱线亮度变化非常小,那么我们就观察不到这条暗线了。这样,我们说处基态的质量为10000000的电子虽然也吸收质量为的光子,但实际上电子对不同质量光子的吸收率不同,所以本来应该产生的9条暗线可能实际上只有3条或4条。这了就是为什么原子的吸收光谱中暗线条数少于明线光谱中亮线条数的原因。
那么,原子发光光谱为什么是明线光谱呢?明白了暗线光谱形成的原因,对于这一点就很好理解了。接前面的假设,我们知道,电子对质量为50、100、250、300、450、500的光子的吸收率大大高于电子对其它质量光子的吸收率,并且因为电子在吸收了上述质量的光子后是比较稳定的,它在新轨道上的存活时间也比较长(它裂变后会放出质量为50、100、250、300、450、500的光子),所以质量为1000050,10000100,1000300,10000500的电子数目总要多于其它质量的电子数。为理解这个问题,我们打个不恰当的比方,假设质量为1000050,10000100,1000300,10000500的电子的存活时间是1000秒以上,而其它质量的电子在原子中的存活时间不到1秒,则经过一段时间的加热后,质量为1000050,10000100,1000300,10000500的电子数目将明显多于其它质量的电子数量,所以电子裂变的产物--质量为50、100、250、300、450、500的光子数目也远远多于其它质量的光子数量,正因为如此,原子的发光光谱中总有特定的谱线特别亮,形成我们所说的明线光谱。
最后,我们的结论是:原子中的电子可以吸收能量连续的光子,也可以发出能量连续的光子,但由于电子对特定质量光子的吸收率大于其它光子,所以在原子的吸收光谱中总有几条特定的谱线显得较暗,形成暗线光谱;大量原子发光时,电子放出特定质量光子的频率大于其它光子,所以在原子的发射光谱中总有几条特定的谱线显得较亮。
8、电子在原子中的运动
借助模型来分析微观原子世界是我们常用的方法,它可以更好地检验我们的假设。深刻认识电子在原子中的运动,不仅对解释原子光谱问题具有决定性意义,而且对于化学将产生极其深远的影响,特别是对于化合价理论、对于我们认识物质的化学变化起到决定性的作用。自从人类认识到原子有内部结构--是由处于中心的带正电的原子核和核外带负电的电子组成的以后,人们就开始探求电子的运动规律。先有卢瑟福提出原子的行星模型,后有电子云模型。撇开卢瑟福提出原子的行星模型不说,先来谈谈电子模型。量子力学的观点指出,在某一瞬间我们不能准确描述电子在原子中的位置。令我想不通的是,电子既然没有摆脱原子核的静电引力,既然还受原子核的束缚,那么它在原子中的位置就不是随意的,因为电子从离核较近的地方运动到离核较远的地方是要克服静电引力做功的,是谁给了电子能量呢?不会是上帝吧?量子力学指出,电子可以出现在离核较远的地方也可以出现在离核较近的地方,但是没有描述这一过程是怎样发生的。既然电子还受到原子核的束缚,它的运动就不是自由的,就要受一定的规律制约,而制约电子运动的主要因素是原子核的静电引力和光子对电子的扰动。电子不是存在于精神世界中,它的运动规律是可以被我们认识的。
量子力学中有一个被称为“薛定谔猫”的著名理想实验:一只猫被置于一个密封的盒子中。有一杆枪瞄准着猫,如果一颗放射性核子衰变就开枪,而发生此事的概率为百分之五十。如果人们开启盒子,就会发现该猫非死即生。但是在此之前,猫的量子态应是死猫状态和活猫状态的混合。量子力学的全部要点是,它对实在有不同的观点。根据这种观点,一个对象不仅有单独的历史,而且有所有可能的历史。在大多数情形下,具有特定历史的概率会和具有稍微不同历史的概率相抵消;但是在一定情形下,邻近历史的概率会相互加强。在薛定谔猫的情形,存在两种被加强的历史。猫在一种历史中被杀死,在另一种中存活。两种可能性可在量子理论中共存。“薛定谔猫”理想实验被一些吹捧量子力学的人视为经典的“圣经”,这里我们暂且不去谈它的哲学意义。我想要明确指出的是:放射性核子衰变虽然有一定的机率,但对于一个特定的核子来说,它的裂变是必然的。就是说,如果我们完全清楚该核子的内部结构,知道其内部各部分之间的作用情况,我们就可以准确确定核子裂变的时间,那么在一定的时刻内,我们就确定核子是否发生了裂变,也能够确定猫的死活。再打一个容易接受的比方,分子运动论指出分子是时刻不停地运动的,每秒钟一个分子与另一个分子会发生许多次碰撞,分子的运动轨迹是十分复杂的,在这一秒钟它可能在这,下一秒可能在那,但是所有的人都不会否认,分子的运动是可以被我们准确描述的。假设我们能够知道分子在每一时刻与其它分子的相互作用,我们就可以准确地描绘出分子的运动轨道(当然,这不太可能也没有必要)。理论上讲,我们可以准确描述每一个分子的运动轨迹,同样我们也可以准确描述原子中电子的运动轨迹。关于“薛定谔猫”理想实验问题的讨论说得再多也是白费口舌,我们不想作无谓的争论,我们需要的是实实在在、有说服力的实验依据,鉴于此,我们来谈谈电子在原子中的运动。
常温下气体分子之间发生的碰撞是非常频繁的,甚至每秒钟可达上亿次之多。而原子中的电子与光子的相互作用也是极其频繁的,恐怕与常温下气体分子之间发生碰撞的频率不相上下。在这么频繁的作用下,电子能够处于稳定状态,的确不容易。而要说清楚电子在原子中的运动也不容易,所以我们有必要借助经典原子理论的一些概念。
在经典理论中,电子的可能轨道是不连续的,设原子中电子稳定存在的轨道分别是R1、R2、R3、R4……Rn,并且有R1<R2<R3<R4<……<Rn,我们知道,电子在这些轨道上的质量不同,设其分别为M1、M2、M3、M4……Mn, 并且有M1<M2<M3<M4<……<Mn,假设在某一时刻电子在距核R1的轨道上绕核旋转,并且我们进一步假设M1、M2、M3、M4对应的质量分别为1000050,10000100,1000300,10000700,而光子的质量从1到1000连续变化。那么对于处于R1轨道上、质量为1000050的电子而言,它可能吸收质量为50、100、300、700的光子而跃迁到离核较远的R2、R3、R4轨道上,电子在这些轨道上是处于亚稳定状态的。这就是说,电子在这些轨道上停留一定的时间后必将裂变放出光子并重新回到原来的轨道上。现假设电子吸收了一个质量为50的光子并跃迁到离核较远的R2轨道上,这时电子的质量变为10000100,根据电子的质量—结合能曲线表我们知道,此时电子的内部结合力变小(但在一定范围内仍然处于峰值),而此时原子核对电子的静电引力也变小,从而电子内部的结合力就可以抵御原子核的静电引力。此时若电子不受到任何扰动的话,这个平衡状态是可以无限维持下去的。但电子总要受到各种各样的扰动作用,若在某一时刻电子受到指向原子核的扰动,并且这个扰动作用足够强,那么电子就要重新回到原来的轨道上,电子回到离核较近的轨道上以后,在原子核强大的静电引力作用下电子内部各部分之间的结合力不足以抵御原子核的静电引力作用,必然裂变放出光子,从而打破了电子和原子核建立的暂时的平衡。电子放出光子以后,质量变小,内部结合力能够抵御原子核的静电引力作用,建立了新的平衡状态,而这个新的平衡状态又会立即被打破,电子就是在平衡--不平衡--平衡中不断运动变化着的,而原子系统主要就是通过电子质量的变化来和外界完成能量交换的。

我们知道,电子从R1轨道上跃迁到R2轨道上再返回R1轨道上需要一定的时间,而这个时间通常我们称为激发态原子的寿命,这段时间的长短和哪些因素有关呢?显然,首先,这段时间和电子在R2轨道上的质量结合能有关,若这个结合能很大,则其对光子扰动的缓冲作用也越强,相应的激发态的原子寿命也自然越长。其次,这段时间和电子受到的扰动有关,电子受到的扰动越强,则这段时间就越短。我们可以想象,若在距核R1的轨道上质量为1000050的电子吸收了一个质量为46的光子,则形成的新电子质量为1000096并将跃迁到离核较远的地方R,我们知道,在电子的质量—结合能曲线表上,质量为1000096的电子其内部结合能是很小的,甚至受到轻微的扰动也破坏电子和原子核之间的平衡,所以电子在离核R处停留的时间极短甚至趋近于零,相应的激发态的原子寿命也为零,换句话说,我们可以认为电子在离核R处的停留时间是零,这样的轨道当然也不存在了,就是说,在原子中不存在离核距离为R的亚稳态的电子轨道。事实上,电子轨道这个提法并不准确,因为电子在原子中的运行轨迹并不是圆或者椭圆,而经典理论中所说的电子轨道其实就是电子内部结合力大、停留时间长的运动区域而已。由于电子时刻不停地受到光子的扰动作用,因而电子的轨道与宏观行星绕太阳运行的轨道完全不同,微观中电子的“稳定轨道”仅仅只能理解为电子在某一特定质量时其内部结合力大、停留时间长的“运动区域”。我们认为“轨道”概念换成“运动区域”更准确的原因就在于即便电子在该“轨道”是相对稳定的,但由于受到光子的扰动作用,电子可能在这一时刻离核近一点,而在下一时刻离核远一点,所以电子的运动轨迹是在某一平衡位置两侧来回摆动的,也正是因为这样,我们把电子“稳定轨道”概念换成“运动区域”,这样能更好地描述电子在原子中真实的运动情况。
经典理论认为,电子吸收了特定质量的光子后会跃迁到离核较远的轨道上,此时电子处于激发态,而在通常情况下电子总是处于某一稳定的轨道上。这种观点是否正确呢?按照我们的假设,电子时刻不停地与光子作用,因而电子始终处于激发态中,这个激发态并不一定就是离核较远、相对稳定的轨道,甚至电子在离核最近的轨道上时也是处于激发态中。这一点怎样理解呢?当电子在离核最近的轨道上运行时,它的运行轨迹也不是一成不变的,光子对电子的扰动作用总是力图使电子偏离原来的运动轨道,电子的质量也因此时刻在发生着变化,电子总是在不断地吸收—放出光子,所以我们说电子始终处于激发态中。至于经典理论所说的激发态是指电子处于离核较远的、电子内部结合能较大的轨道,这个激发态的概念是狭义的,当然也是不够准确的。电子在原子内部时刻都处于激发态之中,电子离核的远近时刻在变化着,但不管怎样,电子与原子核之间的静电作用始终都遵循库仑定律,可以说到目前为止,我们还没有发现电子在原子中的运动违背了库仑定律。
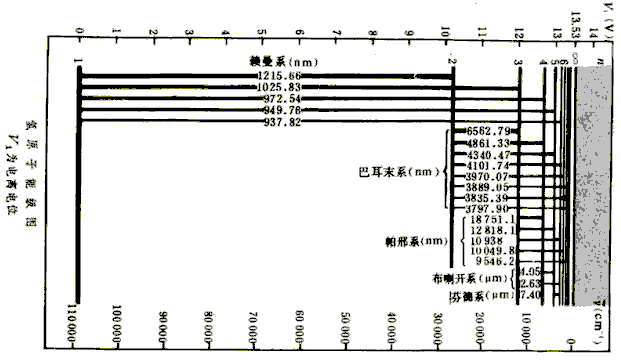
9、原子系统
看了这个题目,可能有人觉得奇怪,原子系统不就是由原子核和电子组成的吗?这有什么好写的?不错,表面上看原子系统的确是由原子和电子组成的,但这只是最初步的定义,没有揭示原子系统的实质。比如,原子系统和太阳系的行星系统有什么区别?为什么宏观点电荷不能模拟原子系统?微观电荷中满足什么条件的粒子可以形成原子系统?等等,这都是本节要研究的课题。这里,我们所说的原子系统,是指电子和原子核形成的、在一定条件下能够稳定存在的系统,这个系统在外力作用下能够恢复到原来的状态。这个系统与宏观行星系统和宏观点电荷是完全不同的。
行星系统或者说人造卫星系统和原子系统的差别在哪里?我们认为主要表现在以下几个方面:一是行星系统中行星轨道的连续性与原子系统中电子稳定轨道的不连续性差异;二是行星系统中行星质量的固定性与原子系统中电子质量的可变性差异;三是行星系统中行星稳定轨道存在不同的离心率与原子系统中电子稳定轨道离心率为零的差异;四是行星系统中作用力的单一性(万有引力)与原子系统中存在多种作用力的差别;五是行星系统的脆弱性与原子系统的稳定性的差异;六是行星系统中行星轨道的平面性与原子系统中电子轨道的空间性差异等等。正是因为以上的原因,所以从理论上来看,不可能用行星系统来模拟原子系统。这两个系统有本质的区别,事实上也的确不能用行星系统来模拟原子系统。下面我们就来具体分析行星系统与原子系统的五大主要差别。
关于行星系统中行星轨道的连续性与原子系统中电子稳定轨道的不连续性差异。我们知道,人造卫星的轨道可以设定,飞行高度可以连续变化,相对于原子系统来说,人造卫星的轨道具有连续性。这就是说,只要我们选择合适的初速度,人造卫星就能够停留在任意高度的轨道上(至少在理论上是这样的)。但在原子系统中,电子的稳定轨道总是与其结合能极大的质量值密切联系着,倘若电子在某一轨道时其质量不是处于结合能极大的峰值上,则电子的这条轨道就是不稳定的,电子在这条轨道上停留的时间很短,以至于我们也可以认为电子没有机会在这条轨道上停留,很自然这条轨道也可以认为不存在了。当今物理学界,有人根据行星系统轨道的连续性认为电子稳定轨道也应该是连续的,对于电子稳定轨道的不连续性,则用物质波来加以解释,进而提出什么测不准关系,其实哪是什么测不准的?行星系统中的行星在某一瞬间有确切的位置,原子系统同样也是如此,在某一瞬间,电子也有其确切的位置,并且只要我们知道了前一瞬间电子在原子中的确切位置、电子运动速度和电子的受力情况,我们就能计算出下一瞬间电子的位置。物质波理论将粒子性和波动性两种截然不同的属性揉在一起,其实是对原子系统认识不够深刻的表现,而测不准关系的出现,无非是认为人们对原子世界是不能够认识的。因为测不准,所以也说不清,最终将导致不可知论。
关于行星系统中行星质量的固定性与原子系统中电子质量的可变性差异。在行星系统中,行星的质量一般是固定不变的,尽管也有的行星可能因为遭陨石撞击而增大质量,但是一般这种变化是不可逆的,也就是说,行星不会在这一段时间增大质量而在另一段时间内减小质量。在原子系统中则不然,电子与光子的吸收、分离过程是可逆的、而且发生的极为频繁。电子可能在这一时段吸收一个光子增大质量并跃迁到离核较远的轨道上,在下一时段电子可能会放出一个光子减小质量并重新回到离核较近的轨道上,电子的质量可以时大时小,或大或小,而在行星系统中这是完全不可能发生的。当然,电子的质量变化相对于电子自身的质量来讲是很小的。
关于行星系统中行星稳定轨道存在不同的离心率与原子系统中电子稳定轨道离心率为零的差异。在行星系统中,行星绕太阳运行的轨道并不是正圆,通常都有一定的离心率。如人们所知,地球的运行轨道就不是正圆,更典型的是哈雷慧星,其轨道的离心率是非常大的。而在原子系统中,由于原子核和电子之间磁力的存在,这个力总是试图使电子的轨道趋近正圆。在以前,当人们用卢瑟福模型解释原子光谱问题时,总是设想当电子轨道的离心率不是正圆时的情形,现在我们知道这个假设是不正确的,因为在原子系统中,并不是只有静电力的作用,还存在原子核和电子之间的磁力作用,所以电子的轨道也不存在所谓的离心率。
关于行星系统中作用力的单一性(万有引力)与原子系统中存在多种作用力的差别。在行星系统中,太阳和行星之间存在着唯一的一种作用力━━万有引力,这个力是使行星绕太阳运行的唯一因素。只要行星有一定的初速度,它就可以在一定的轨道上绕太阳运行,形成行星系统的条件是有万有引力并且行星有一定的初速度;特别是在人造卫星系统中,人们可以给人造卫星以不同的初速度从而使其按人们的设想停留在特定的轨道上。而在原子系统中,则有多种作用力的存在。首先是原子核和电子之间的静电引力,这个力总是使原子核和电子相互靠近,其次是原子核和电子之间的磁力作用,这个力总是试图阻止原子核和电子相互靠近,事实上原子核和电子主要是在这两种力的作用下维持着平衡。除了这两种力的作用以外,在原子系统中,电子之间的静电斥力也是必须考虑的一种力的作用。
关于行星系统的脆弱性与原子系统的稳定性的差异。对于行星系统来说,其稳定性极差,外界任何一种力的影响都足以破坏已经存在的平衡。比如说地月系统,随着地球转速的逐渐减缓,月球也在逐渐远离地球,并且这一过程是不可逆的,有科学家预言,月球最终将脱离地球。又如在人造卫星系统中,尽管人造卫星所处的空间大气很稀薄,但对人造卫星的阻力仍然不能忽略,这个阻力的存在使人造卫星的速度逐渐减小并最终落到地面上,所以人造卫星总是有一定的寿命,换句话说,人造卫星系统是不稳定的,在没有外力的影响,卫星和地球所形成的平衡最终要被打破。而在原子系统中,电子时刻受到光子的扰动,这个扰动有指向原子核的也有指向核外的,在这个扰动下,电子可能远离原子核也可能离原子核更近,但无论如何,电子总能够回到原来的位置。一般情况下,电子在原子中是足够稳定的,但倘若电子受到的扰动极大,这个稳定状态就要被破坏。如电子受到强紫外线照射时,因为光子的能量极大,就可能将电子电离。
关于行星系统中行星轨道的平面性与原子系统中电子轨道的空间性差异。在太阳系中,每个行星的运行轨道形成一个平面,九大行星的运行所形成的轨道都大致在同一平面上,所以可以认为在行星系统中,行星的运行轨道是二维平面的(虽然也有的行星的运动平面可能与公共平面之间有一定的夹角,但通常这个角度都很小,如地球的黄赤交角)。事实上,在以万有引力为主要作用力构成的系统中,除太阳系以外,绝大多数星系也是盘状而非球状的,就我们熟悉的银河系,它就是盘状的,可以认为大部分物质都是分布在同一个平面内的,而不是均匀分布在以银河系的中心为圆心的球面内的。但在原子系统中,电子的运行轨道却不是在平面中,而是在三维球面空间中,通常情况下,电子的运动区域是在以原子核为圆心、两个不同半径圆面之间的区域。
正是基于以上的原因,我们把行星系统称为低级系统,而把原子系统称为高级系统。我们说行星系统属于低级系统,就在于维持行星系统的作用力单一,行星系统不具备轨道修复能力,而且往往有一定的寿命,但由于行星系统的质量往往很大,所以其寿命也很长。而原子系统则由于其质量极小,状态极易改变,所以需要一个以上的力来维持其稳定状态,比如说,原子系统具备轨道修复能力,其寿命可以是无限长。原子系统和行星系统之间的差别是构成宇宙的必要条件,试想,如果行星系统非常稳定,寿命很长,而原子系统非常不稳定,寿命小于行星系统,那么由原子组成的物质本身就是不稳定的,所以行星系统也不可能是稳定的,这样就不可能形成我们今天所看到的丰富多彩的宇宙。
以上我们讨论了原子系统和行星系统的差别,指出不能用行星系统模拟原子系统。现在我们来看宏观点电荷和微观原子系统的差别。我们认为主要差别有以下两点:一是宏观点电荷荷质比极小与微观原子荷质比极大的差别;二是宏观点电荷质量固定与原子系统中电子质量可以变化的差别。因为宏观点电荷荷质比极小,所以在静电力作用下其获得的最终速度也很小,电荷间的磁力作用可以忽略,这就造成宏观点电荷之间的静电作用相当简单:或者分离或者吸引在一起。所以完全不能用宏观点电荷模拟微观原子系统。假如有人说,我非要用宏观点电荷模拟微观原子系统,比如找到两个荷质比非常大的带异种电荷的宏观点电荷(假设能够做到),那么它们能不能形成稳定的原子系统呢?我们说也不能。如果这两个点电荷的荷质比非常大,因为宏观点电荷的质量是固定的,它们也不能形成稳定的轨道。在原子系统中,正是因为电子质量的可变性,为外力扰动提供了缓冲,而在宏观系统中,这是做不到的。
前面我们讨论了行星系统、宏观点电荷与原子系统的差别。在原子系统中,与原子核相比,电子的质量要小得多,不到整个系统的1%,而原子核占了原子系统99%以上的质量。在微观中有没有和原子一样的系统呢?这就是说,如果带正电荷的微粒不是原子核、带负电的微粒不是电子的两个粒子能不能形成类似原子系统的稳定存在的系统呢?如果能,满足什么条件呢?如果不能,又是为什么?我想可能有相当多的人都很关心以上问题,它将为我们彻底研究原子光谱问题打下基础。理论上指出,在微观粒子中,只要两个粒子的荷质比足够大,都有可能形成原子系统,当然这仅仅只是可能而已,就是说具备了原子系统的最起码条件。那么是不是任意两个粒子都可以形成原子系统呢?也不是的,它们必须带异种电荷。废话!还有,它们的质量必须有一定的差距,两个质量一样的点电荷是不可能形成稳定的原子系统的。那么,它们质量差距究竟是怎样的呢?是相差10倍、100倍、1000倍还是更多或者是越多越容易形成原子系统呢?坦率地讲,这一点目前我们还没有办法回答。我们只能给出什么样的微观带电粒子不能形成稳定的原子系统,但却不能准确地定义什么样的微观带电粒子一定能形成稳定的原子系统。
10、回顾与展望
氢原子和类氢原子电子都有相似的轨道,其光谱都可以用玻尔理论来描述,这说明电子质量“幻数”的确存在。那么,决定电子裂变的因素是否只有原子核呢?不是的。如果是的话,那么所有的元素都应该有相同或相似的光谱,然而事实并非如此。在多电子原子中,一个电子是否裂变取决于原子核和其它电子的共同作用。内层电子的存在,在一定程度上屏蔽了原子核对外层电子的作用,而外层电子的存在,也对内层电子的裂变有一定的影响。正因为如此,多电子原子光谱比氢原子和类氢原子光谱复杂的多。要想分析多电子原子光谱规律,首先必须确确实实地画出电子的质量━━结合能曲线表。如果我们能够准确地绘出电子的质量━━结合能曲线表,那么我们就在解决原子光谱问题上迈出了具有决定意义的第二步。我们知道,电子带负电荷,并且电子在原子中时刻不停地运动着,所以电子内部结合力也受到电场、磁场的影响,要准确描述原子光谱,电场、磁场的因素都要考虑进去。对于多电子原子而言,内层电子的轨道比起外层电子来说相对稳定,考虑外层电子的运动情况,不仅要考虑原子核的影响,更要考虑内层电子的静电斥力和磁力作用,这些力中哪一个占主导作用要视具体情况而定,而不能简单地认为内层电子仅仅起到了屏蔽原子核静电引力的作用。那么多电子原子光谱遵循怎样的规律呢?这里只能说的是,目前我们的模型还不够完善,想要真正解决多电子原子光谱问题,还要经过不懈的努力。鉴于多电子原子光谱的复杂性,我们将在开天辟地的第二版中初步探讨多电子原子光谱模型。
Email:txj731@163.com
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑