物理科学探疑-网友天空-系统观点-李学生-一、时空平权理论
一、时空平权理论
李学生
摘要:
本文回顾了时空观的演变，分析了时空平权理论的背景，从唯物辩证法的观点出发，依据相对论的理论基础，发展了时空平权问题，把时间单位与空间单位统一起来，使国际7个基本物理量减少为6个，在此基础上根据量纲推导出质能方程。
关键词：时空平权、相对论 、质能方程、时间与空间、国际基本物理量
（ 一）、时空观的演变
从逻辑的、分析的角度看，时间的确具有与空间相似和相同的特性，这使得哲学史上大多数哲学家都把空间和时间放在一起讨论。空间和时间是事物之间的一种次序，空间用以描述物体的位形；时间用以描述事件之间的先后顺序。柏格森第一次从哲学上对时间和空间进行区分，并把时间置于比空间更优越的地位，这具有划时代意义。时间本体从空间化的时间中突现出来。后来的时间哲学不论是现象学、存在主义还是怀特海，都继承了时间优于空间的思想，这导致时间不论在作为物的存在方式，还是作为人的存在方式，都获得比空间更为根本的意义。
空间和时间的物理性质主要通过它们与物体运动的各种联系而表现出来。在自然科学中，时间已不仅作为一个度规量而与空间一起接受几何学、逻辑学考究，时间的不可逆性和方向性本来就是一个重要的科学哲学问题，赖兴巴赫和格鲁巴姆为解释时间的方向性作出了重要的贡献。在物理学中，对空间和时间的认识可以分为三个阶段：经典力学阶段、狭义相对论阶段及广义相对论阶段。在经典力学中，空间和时间的本性被认为是与任何物体及运动无关的，存在着绝对空间和绝对时间。牛顿在《自然哲学的数学原理》中说：“绝对空间，就其本性来说，与任何外在的情况无关。始终保持着相似和不变”“绝对的、纯粹的数学的时间，就其本性来说均匀地流逝，而与任何外在的情况无关”。另一方面，物体的运动性质和规律，却与采用怎样的空间和时间来度量它有着密切的关系。相对于绝对空间的静止或运动，才是绝对的静止或运动。只有以绝对空间作为度量运动的参照系，或者以其他作绝对匀速运动的物体为参照物，惯性定律才成立。即不受外力作用的物体，或者总保持静止，或者总保持匀速运动。这一类特殊的参照系，被称为惯性参照系。任何两个不同的惯性参照系的空间和时间量之间满足伽利略变换。在这种变换下，位置、速度是相对的，即相对于不同参照系其数值是不同的：长度、时间间隔是绝对的，即相对于不同参照系其数值是不变的，同时性也是绝对的。相对于某一惯性参照系同时发生的两个事件，相对于其他的惯性参照系也必定是同时的。另外，牛顿力学规律在伽利略变换下保持形式不变，这一点符合伽利略相对性原理的要求。正是这个相对性原理，构成了对牛顿的绝对空间概念的怀疑的起点。如果存在绝对空间，则物体相对于这个绝对空间的运动就应当是可以测量的，这相当于要求在某些运动定律中含有绝对速度。然而，相对性原理要求物体的运动规律中必定不含有绝对速度，亦即绝对速度在原则上是无法测定的。莱布尼兹、贝克莱、马赫等先后都对绝对空间、时间观念提出过有价值的异议，指出过没有证据能表明牛顿绝对空间的存在。
Einstein是二十世纪最伟大的科学家，在一本曾被称为“由本人系统地阐述相对论的唯一著作”《相对论的意义》一书中，Einstein开门见山第一名话就是“相对论和时间与空间的理论有密切的关系”，在Einstein相对论的所有推理过程中，都离不开时间和空间的性质，虽然其所表述的高速世界运动规律的科学结果与我们日常生活所感觉到的是多么的不同，但这是科学。
Einstein的相对论不仅标志着人类科学思维的一大进步，而且是我们今后相当一个时期科学发展的新的起点，是值得我们进一步思考下去的通向新的辉煌的通道。因为，这里讨论的本质上是关于时间和空间的理论，这几乎是一切科学的基础。
Einstein推广了上述的相对性原理，提出狭义相对论的相对性原理，即不但要求在不同惯性参照系中力学规律具有同样形式，而且其他物理规律也应如此。在狭义相对论中，不同惯性系的空间和时间之间遵从洛伦兹变换。根据这种变换，同时性不再是绝对的，相对于某一参照系为同时发生的两个事件，相对于另一参照系可能并不同时发生。在狭义相对论中，长度和时间间隔也变成相对量，运动的尺相对于静止的尺变短，运动的钟相对于静止的钟变慢，光速在狭义相对论中是绝对量，相对于任何惯性参照系光速都是c。经典力学和狭义相对论都认为一个惯性参照系可以适用于整个宇宙，或至少一个大的范围。相对于某一个惯性参照系，宇宙中任何范围中的物体运动都遵从惯性定律。实际上，空间化的时间可以与空间一起处理。在时间空间化最为明确显著的近代物理学中，时空完全是作为一体的。在牛顿运动方程中，时间t如取负值，方程依然可以成立，表明牛顿力学是时间可反演的；在Einstein狭义相对论中，时间的空间化进一步被形式化、完备化，时间、空间成为时－空。
Einstein在广义相对论中指出，如果考虑到物体的万有引力，一个惯性参照系只能适用于一个非常局部的范围，不可能适用于大的范围，或全宇宙。如果对于描写一个局部范围中的物体来说，某一参照系是惯性的那么对其他范围中的物体运动而言，它一般就不再是惯性的。为了描写在一个大范围中的运动，对不同局部范围要用不同的惯性参照系。物体之间的引力的作用，就在于决定各个局部惯性系之间的联系。用几何的语言来说，各个不同的局部范围的惯性参照系之间的关系，可以通过时空曲率来规定。引力的作用就在于使空时变成弯曲的，而不再是经典力学中的无限延伸的欧几里得几何的绝对空间，也不再是经典力学中的无限延伸的闵可夫斯基空间。总之，在广义相对论中，时空的性质不是与物体运动无关的。一方面，物体运动的性质要决定于用怎样的空间时间参照系来描写它另一方面时空的性质也决定于物体及其运动本身。
量子论的发展，对时间概念提出了更根本的问题。量子论的结论之一就是：对于一个体系在过去可能存在于什么状态的判断结果，要决定于在现今的测量中做怎样的选择。所以，除非一个体系的过去状态是已经被记录到了这种情况以外，不能认为体系的历史是独立于现今的选择，而存在于过去的时间中的。量子力学提出时间量子化问题。
这种现在与过去之间的相互关系，是与因果顺序概念十分不同的，暗含于时间概念中的因果序列要求过去的存在应是不依赖现在的。另外，量子论还表明，
这样小的时空尺度中，描写事件顺序的“前”“后”概念将失去意义。
因此，用时间来描述事件发生的顺序，可能并不总是合用的。空间与时间是事物之间的一种次序，但并不一定是最基本的次序，它可能是更基本的次序的一种近似。
（二）、时空平权理论的背景
Engles认为，从宇宙总体上来看，物质运动是一个永远循环的过程，在这个循环过程中，物质的任何一个属性都不会丢失。宇宙的每一循环过程都按照物质固有的规律运行，是物质属性的有秩序的展现过程，循环过程中的物质运动规律是永恒不变的。世界的某些特征永远保持不变。自然定律在空间的每一个方向上以及在任何时刻都相同，这分别等价于在任何物理过程中的总旋转量——角动量——守恒和总能量守恒。这两个量与电磁质量的总体绝对守恒，它们作为守恒量已与整个物理学的上层建筑深深缠结在一起了。因此“无限时间内宇宙的永远重复的连续更替，不过是无限空间内无数宇宙并存的逻辑的补充③”，即时间内的宇宙是空间内的宇宙的纵向展开。所以，“物质在它的一切变化中永远是同一的，它的任何一个属性都永远不会丧失。因此，它虽然在某个时候以铁的必然性毁灭自己在地球 上的最美的花朵——思维着的精神，而在另外的某个时候一定又以同样的铁的必然性把它重新产生出来。③”物质的每一个循环过程都是其前一循环过程的重复，各个循环过程所包含的信息展现的程序也是相同的，时间是空间的变化，时间经常是用事物变化的方式来定义的。
关屹瀛先生提出了宇宙量守恒原理：宇宙量形式为
，(G为宇宙量，X(x)为宇宙量的空间形式，T(t)为宇宙量的时间形式，K为常数)，宇宙量的具体形式之一:
，（G为宇宙量，L是米的量纲，M是质量的量纲，T是时间的量纲）。纵观各物理量的量纲会发现，凡是在封闭的系统中守恒的量，几乎无一例外的是上述形式。比如：当n=1时，这正是动量的量纲。而动量守恒定律的应用是极其广泛的，小到微观粒子，大到宇观星体。当n=2时，宇宙量为能量量纲，而能量守恒定律也是应用极其广泛。“能量”一词，已成为遍布所有领域中的最基本的概念之一。
Galileo相对论指出，不存在“静止状态的”绝对意义，所以“在不同时间的空间的同一点”是没有任何意义的。狭义相对论揭示了作为物质存在形式的空间和时间在本质上的统一性，时空不能截然分开而是统一的整体，但是没有指明时间与空间的本质。不同时刻的三维Euclid空间被分开，把这些空间合并在一起构成了完整的四维时空图。在狭义或广义相对论的情形下，时间应当是同时性空间或类空表面。在空间——时间中进行匀速直线运动的粒子历史是一条直线——世界线。不变的不是时间间隔和空间间隔，而是时空线元长,
广义相对论具有宇宙因子项重力场方程的普遍形式
是物质的能量—动量张量；k为常数，可由泊松方程求得，λ为宇宙因子，等式的左边是描述空间几何性质的几何量，而右边是物质张量。该式把物质和时空紧密联系在一起，表明空间——时间的几何性质与物质的分布及其运动密切相关，物质的分布和运动决定四维空间的曲率，而这个弯曲空间又决定物质的运动状态。广义相对论进一步揭示空间与时间的统一性，指出空间和时间不可能离开物质而独立存在，空间的结构与性质取决于物质的分布，因此时间与空间相结合的时空才是物理实在，时间与空间分别是时空的投影。空间是时间的沉淀（绝对的时间），时间是空间的流动（绝对的空间），二者无法真正分开。时间量子和空间量子是完全融为一体的，二者包含着相同的信息，只是其形态不同：一动，一静。时空全息律表明，时间量子与空间量子是相互包含的，而空间量子与空间整体全息，所以时间量子与空间整体也是全息的，反之空间量子也与时间整体全息。时间量子与空间量子的结合体就是时空量子。时间不过是纵向的空间，空间则是横向的时间；空间是静止的时间，时间是运动着的空间，二者实为一体的东西。在物理学中，在任何惯性参考系中观察任意两个事件，其时间的先后次序都具有绝对的意义，时空中任意两点间的内禀距离只能是一个旅行者从一点到另一点所花费的固有时间。对于绝对时间与绝对空间而言，事物在空间上的分布规律是其在时间上分布规律的反映，例如宇宙间天体系统的空间分布是其时间演化层次的横向分布，现在空间上的宇宙是历史上宇宙的一个缩影。时间和空间的结合形成时空连续统，绝对时空连续统的表现形式是相对时空连续统。
（三）、时空平权理论
Einstein所构建的四维时空连续统是相对时空的一个特例。对于四维时空，尽管时空间隔的度规方程是按照空间度规为标准的，但符号的正负不定，是可变的，所以叫做符号不定的度规。狭义相对论的时空就是符号不定的度规的时空。绝对时空是无限的。绝对空间和绝对时间在无限中达到了绝对的统一，绝对时空不受任何条件的制约，绝对独立，绝对连续，绝对均匀，绝对统一，绝对不动，绝对全息（1）。有人认为尽管相对论中空间和时间是密不可分的，然而时空的类时性或类空性还是绝对的，但是事件具有虚值时间坐标的空间——时间称为Euclid型的，在Euclid时空图中，时间方向与空间方向没有不同之处，空间与时间是一个问题的两个方面。Minkowski方程反映了时空平权问题，他认为：“这种对称性在数学上可以用意义很深刻的神秘形式反映相对论的本质（Minkowski称为绝对世界的标准）。”设光速c=bm/s，由于光从A点到B点走1s与走bm是一样的，因此若令光速为1，则得1s=bm ，场的运动速度为1。时间用空间的变化来测量，空间用时间的变化来测量。光年既是时间单位，也是长度单位。在经典广义相对论的实时时空中，因为时间只沿着一位观察者的历史增加，不象空间那样可以沿着历史增加或减少，时间和空间方向可以区分开来；但是在量子力学虚时间方向和空间方向一样，可以增加或减少，经常使用“将时间变为空间”的问题，在任何情况下，我们利用虚的时间和Euclid空间——时间可以认为仅仅是一个计算实空间——时间的答案的数学手段（或技巧），在计算机技术中也存在这个问题。对于我们的量子边界，我们需要四维空间——而不是四维时空——中的一个三维表面。因而Stephen Hawking和James Hartle提出：在量子宇宙学格局中，通常的时间概念不再适用，它变成了又一维的空间。空间的几何学可以用来作为时间的量度。在量子宇宙学中，时间是宇宙中的物质成分及其位形的构成物。（4）宏观世界里物体的运动速度很小，仍可用m/s表示。这样便将国际基本物理量缩减为6个。若将光速定为1，则物体的速度称为物体的相对速度，速度是物体在相对时空中空间与时间的比值。我们称之为时空的平权理论，它是时空对称的绝对性的表现形式 。在微观理论中，特别是基本粒子理论中常取自然单位制，其中把时间与空间的量纲取得相同，并把质量量纲取为时空量纲的倒数，从而只剩下一个量纲，至于单位的大小，则取得使c=1和约化普朗克常数等于1，至于具体取什么单位，则无统一规定，在基本粒子理论中通常是取得使μ介子的质量数值为1。在量子力学中波函数所描写的是处于相同条件下的大量粒子的一次行为或者是一个粒子的多次重复行为，也说明了时空平权的问题。在(2)中王仁川先生也把光速定义为1，笔者认为它进一步表明Minkowski方程的正确性，相对论与量子力学以及基本粒子理论都说明了时空平权理论的正确。
根据时空平权理论，四维时空也可以称为四维空间或者四维时间，空间的多维性导致了时间的多维性，因此物理学中引入向量。唯物辩证法认为时间是指物质运动和发展过程中先后的顺序和持续性，空间是指物质存在的广延性、伸张性，是物体之间的排列角度与排列顺序，分别是一维、三维的，具有一定的时代局限性。根据对称的相对性与绝对性原理，时间与空间既是对称的，又是不对称的，空间量子具有isotropy，时间量子具有anisotropy，这是时空对称性的相对性的表现形式 。遗传和变异分别是时空对称的绝对性与相对性的表现形式。
关屹瀛时空对立统一原理： ，(X(x)为宇宙量空间形式，T(t)为宇宙量的时间形式)。
时间和空间是对立又统一的矛盾关系，是既对立，又相互依存，相互转化的，是统一于同一种物质中，是同一种物质的不同存在形态。它们的变化呈反比例关系。下面我们通过对无穷大量与无穷小量的矛盾关系的证明，给出矛盾双方的普遍反比例关系1。
结论：无穷大量与无穷小量呈反比例关系。同理，时间和空间也呈反比例关系。
由时空量的差别产生的效应，总可以通过时间量的差别来完成。反之由时间量的差别产生的效应，总可以通过空间量的差别来达到。比如，光的干涉实验，当只允许单个光子通过时（此时空间量小），短时间暴光，则在底片上只产生几个光斑，不能形成干涉图样。若长时间暴光（时间量存在了差别），则在底片上可产生干涉图样。如果不增加时间，只是允许大量光子（空间量存在差别）同时通过小空，那么短时间暴光，也得到了光的干涉图样。
再如，天气预报主要是通过对大尺度空间（水平和垂直）气象条件的探测，来预报未来的天气情况。如果预报未来的时间越长 ，就要求对空间探测的尺度越大。可以说：对时间尺度的预报，依赖于对空间尺度的了解。
再有，考古学家就是通过对地层的研究来推断以前的历史情况。地层越深，可推断出该年代就越久远。上述是时空平权理论的实际应用。用公式表示：
上式的物理意义是：对某一物质而言，若其空间量有了变化（如体积变化），那么该物质必然会产生某一过程；反之，若某一物质产生了某一过程，其结果必然存在空间量的变化。
（四）、质能方程的推导
根据功的原理E=W=Fs=mas，令E=1J，m=1kg,s=1m,a=1m/s2,得1J=1kg×1m/s2×1m=1kg×m2/s2=1/b2kg,所以1kg=b2J，即E=mc2，Einstein的质能方程成立。质能方程的推导简化了，各种简化的形态是科学本身的基础，并且表现为认识过程得以实现的必要条件。质能方程也可以从单位换算中得到，能量的单位也可以用kg表示能量是时空与实物粒子的相互作用 ，Einstein的质能方程反映了时空平权问题，揭示了时空结构对物质的作用，与物质自身的性质无关，惯性质量在这里仅仅起比例常数的作用，而且Einstein也曾经利用狭义相对论的原理、动量守恒定律、辐射压力的表示式以及光行差的表示式，而没有利用它的形式结构推出质能方程（5）。证明如下：
“比如，我们考虑另外一个思维实验，它可以从下图（图2）中方便地想象出来。它是图1中一个部分的放大。图中A和B还是相对作匀速V运动的两个平台。在它们之间的空间中有一个自由漂浮的物体Q，从平台观察，它是静止的。我们在各个平台上都建立一个Z-坐标框架来规定Q的位置。
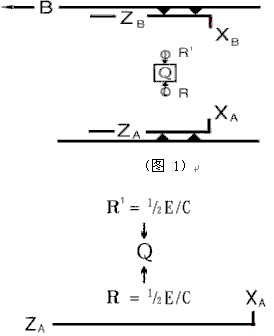
（图 2）现在研究，如果两个等同的辐射束R和
轴的直线向着Q运动，并被Q所吸收，这时会发生什么情况？我们可以先从平台A的观点，再从平台B的观点来分析这一过程。我们将始终记住相对论假设——物理定律对各个空间飞行器都是等同的，尤其是动量守恒定律在每组坐标轴上都是有效的。在辐射被吸收以前，相对于
轴，Q是静止的。自从有了麦克斯韦电磁理论，人们已经认识到能量E的辐射所携带的动量等于E/C，这里C是光速。如果我们赋予每一辐射束R和R1一份能量为1/2E，则动量为（1/2）E/C，那么被Q吸收的辐射可以设想为：由于每个辐射束以垂直于
轴的相反方向击中Q，所以Q相对于
轴显然保持静止。
现在我们从平台B的观点来看同样的过程。参照这个平台，平台A上的物体都是沿ZB轴以与速度V的负方向运动的。
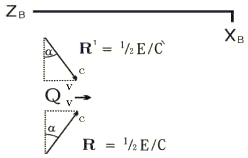
辐射束R和
轴形成角α。正像上图解所表示的，对于小的角，α=V/C有很好的近似。从前面用平台A上的坐标
被Q所吸收，它相对于A的速度（在这里是零）仍然不变。因此，现在用坐标系
被吸收以后也保持不变。
引入狭义相对论假设，并把它应用于动量：动量守恒定律对每个平台（A或B）都有效。尤其是，相对于平台B，我们写出一个辐射被吸收前的表达式，再写出一个辐射被吸收后的表达式，然后令它们相等。由于Q的运动与
轴平行，我们须要考虑沿这个轴的R的动量分量和
之和加上物体Q的质量M，得到吸收前的动量=2[0.5×E/C×V/C
]+MV ①，这里用V/C代替角α。在辐射被吸收之后。吸收后的动量=（吸收后的质量）（吸收后的速度），但是我们在平台B上看到物体Q的速度V一定保持不变，因为平台B相对于平台A继续以相同的速度V运动，不受空间中物体Q吸收辐射的干扰。所以，如果动量守恒定律有效，那么MV+EV/C2
=（辐射吸收后的质量）× V ①，由于E，V和C2都是正数，我们不得不作出结论：辐射吸收后的质量M1，比吸收前的质量大。明确表达为
M+ E/C2 =M1 ①，或 E=（ΔM）C2
①，即，质量改变直接与能量吸收成正比例。如果选择适当的M和E的单位，我们可省略Δ，得到质-能等当公式的熟悉形式：E=mc2
”②
根据时空平权理论可知，引力质量不仅意味着能量，同时意味着动量。假设一物体的引力质量为m，那么它的引力动量应当为mc，即P=mc，不妨称之为引力动量方程，把静止物体的引力能量与引力动量称为绝对引力能量与绝对引力动量，它们都是数量。在物理学中所讲的引力能量与引力动量应当分别为它们的空间量子与时间量子形式。由于引力能量反映了引力质量的空间量子存在形式，空间量子各向同性，因此引力能量是数量。由于引力动量反映了引力质量的时间量子存在形式，时间量子各向异性，因此引力动量是向量。
参考文献：
1、《宇宙全息统一论》王存臻、严春友 著 山东人民出版社 1995年版
2、《广义相对论引论》王仁川 著 中国科学技术大学出版社 1996年版
3、《自然辩证法 》第23-24页 Engels 著 人民出版社1971年版
4、《宇宙的起源》
5、《Einstein晚年文集》Einstein 方在庆 韩文博 何维国 译 海南出版社
2000年3月第1版
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑