物理科学探疑-网友天空-系统观点-董银立-关于机械波和电磁波的研究
![]()
关于机械波和电磁波的研究
董银立
摘 要:经典电磁理论是建立在“完全电磁弹性”模型之上的,因此不适用于高频电路,只有建立在“完全电磁惯性”模型之上的电磁理论才能完美的解释电磁波。
第一节 机械波的研究
按我们第二篇文章的观点,加速运动的电子不向外辐射能量,那么电磁波是如何产生的呢?我们先从机械波说起吧。
按照人们对事物的认识规律,在牛顿创立动力学之前,早已产生了静力学,静力学中有一个重要的定律,即胡克定律:f=-kx,即作用在弹性物体上的力与其形变量成正比。但我们有了动力学的知识后(如:a=F/m或s=at2/2),我们就会发现胡克定律并非一个广泛的真理。因为胡克定律与牛顿定律正好相反,它是建立在完全弹性模型之上的,牛顿运动定律是建立在完全刚性模型(即完全惯性模型)之上的,而宇宙中不存在只有弹性而无惯性的物质,包括电场和磁场。
胡克定律:f=-kx中,f(力)与x(形变)并非瞬时对应关系。当然经典物理也不认为它们是瞬时对应关系,并且把该定律归为静力学之下,这正是经典物理可以正确解释机械波的原因。我们举个例子:我们的手用一个周期性变化较慢的力作用在一个弹簧上时,我们会发现,当手上的力最大时,弹簧的形变量最大,当手上的力为零时,弹簧的形变量为零,于是我们可以得到如下图象:
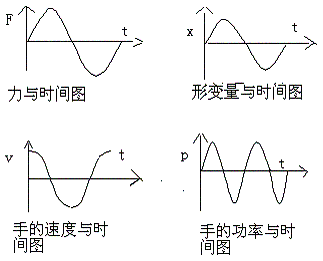
我们的结论是:手的平均功率为零,无论手如何努力,也不会创造出机械波。但我们必须明白,我们使用的完全弹性模型,没有考虑弹簧的惯性。
我们再举个例子:我们的手用一个频率很大的力作用在同一弹簧上,我们发现,当手上的力最大时,弹簧的形变量却是零(即手的作用点位于弹簧不受力时的位置上),当手上的力最小时,弹簧的形变量却最大,我们发现弹簧这时只有惯性而无弹性,胡克定律完全不适用了。于是我们得到如下图象:
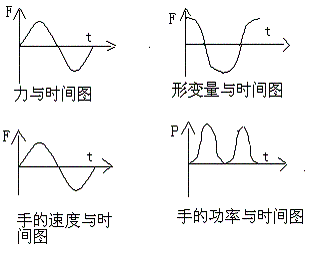
我们的结论是:手的平均功率为最大功率时的一半,机械波产生了!
我们研究机械波时不能使用胡克定律,而只能使用牛顿运动定律及微积分,我们以绳波为例来证明,我们仍用手来提供外部策动力,如下图:为一波形图,从波源O到第一个波
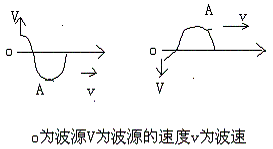
峰或波谷A处,这段绳中所有质点的加速度都是由手上的力提供的,为什么仅仅是这部分质点呢?原因是绳子中A处的张力为零或至少在与波速垂直的方向上即所有质点加速度的方向上的张力为零。又因为这些质点的加速度的大小与该质点离开平衡位置的距离成正比,因此我们推出重要定律:外界(手)对波源的策动力与下图所示阴影部分的面积成正比。从图象上我们可以看出,1图的面积最大,
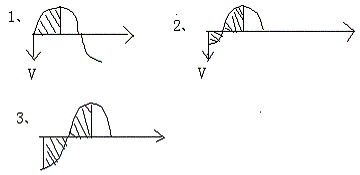
3图的面积为零,可见手在平衡位置处时(或速度最大时)受到的阻力最大,手在最大位移处时(或速度为零时)受到的阻力为零。该结论同样适用于电磁波,并将对电磁波的研究具有重大的指导意义。
第二节 经典电磁理论的局限性
人民教育出版社的《电磁学》中言:“麦克斯伟总结了电磁场的规律,并加以补充和推广。除了涡旋电场和位移电流假说外,他还假设电学的高斯定律和磁学的高斯定律在非稳条件下仍成立,这样就得到在普遍情况下电磁场必须满足的方程组。”该书中又言:“频率再高,似稳电路中一些基本概念(如电压)和基本定律(如基尔霍夫定律)开始失效,到了微波波段,似稳电路的成立条件彻底破坏。”该书自相矛盾的说法似乎已经说的很清楚了,即麦克斯伟不应假设电磁学的高斯定律在非稳条件下仍成立。我们有必要研究清楚麦克斯伟及其以前的整个电磁理论是建立在什么假设之上的,它们是否可以在非稳条件下推广。
模型假设 仍在上述《电磁学》中言:“电容上电压的位相落后于电流的π/2,其根源在于任何瞬时电压都和电量成正比。”事实上经典电磁理论认为某一电容器两端的电压与其两极电量之间的关系为U=kQ,其电场势能与电量的关系为We=kQ2,这是无可非议的,但如果认为电容器两端的瞬时电压都和电量成正比就是错误的,正如弹簧两端的压力与弹簧的形变之间的关系为F=ks、弹性势能与形变之间的关系为W=Ks2一样,但经典力学并不认为弹簧两端的瞬时压力与形变成正比,因为经典力学知道,只有弹性没有惯性(及密度为零)的弹簧是不存在的,只有在某些不必考虑弹簧惯性的特殊情况下,如:在机械振荡中,我们只考虑振子的质量,而不必考虑弹簧的质量的情况下,才能近似的认为瞬时压力与形变成正比。对于电磁场来说,事实上只有当电容器只有电容性而无电感性时,经典电磁理论的观点才正确,然而电容器实质上是位移电流,而位移电流与传导电流一样,都能产生反电动势,都具有电感性(电磁惯性),绝对的纯电容元件和纯电感元件是不存在的,可见经典电磁理论是建立在完全电容性(电磁弹性)这个模型假设之上的,因此它只能完美的解释电磁振荡,却不能解释电磁波(它只相当于胡克定律),因为在电磁波中,电容器(实质上是位移电流,涡旋电场也是位移电流)当只表现为电感性而不存在电容性。
正如牛顿运动定律是建立在刚体模型(或完全惯性模型)上的一样。我们应把电磁场方程组建立在完全电感性模型上,其形式如下:
![]() ,
, ![]()
由此,我们得出的电磁波的图象为:
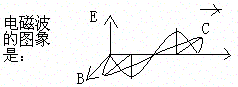
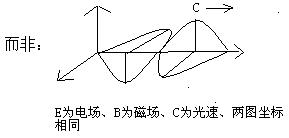
此时刻(上图所视时刻),振源O处发射塔中的电流 I 方向向上,且电流强度为最大值,但振源O处的磁场强度却为零(如上图所视)。但经典电磁理论以完全电容性为模型得出的结论却是:电流周围的磁场强度与电流强度成正比。此时刻,外界向发射塔提供的策动电压U方向向上切为最大值,但此时刻O处磁场激发的“自感阻尼电动势”方向向下,且也为最大值,发射塔中电子受到的合外力仍为零。请注意:该“自感阻尼电动势”并非“电磁惯性阻尼”,因为该时刻电子的加速度为零(瞬时发射功率却最大)!而并非电子的质量为无穷大。此时刻,发射塔的瞬时功率为最大值,其值为 U×I。
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑