物理科学探疑-网友天空-系统观点-尹保华-电荷与电荷间作用力
电荷与电荷间作用力
（《质量—光子物理学》中电磁部分摘录）
尹报华
1.质量微粒模型
客观世界是在一定时间内保持相对稳定的空间关系的各种物质形态。综合物理学尤其是粒子物理学的既有成果，我们作出如下基本假说：1，物质的各种形态，最终可以归结为质量数不同的各种质量微粒；2，任何质量微粒都是密实的、极化的；3，质量微粒的极化性质有三种，即中性极化、正极化和负极化，在电性上分别体现出电中性、正电性和负电性。中性极化又称为匀质极化，正极化和负极化都称为非匀质极化；4，有些质量微粒具有自旋动量矩。
2.相对静止非匀质极化质量微粒间的作用
—电荷间库仑力
相对静止的非匀质极化质量微粒之间存在着相互作用，表现为引力作用或斥力作用。这种作用的实质是非匀质极化质量间的相互极化作用，我们定义这种质量微粒间极化为感应极化，感应极化的作用称为感应。感应是相互的且量值相等。
感应的独立作用原理（叠加原理）：相互静止电荷之间的电作用的性质和强弱由各自的固有极化性质和集度（即电荷数）决定，不因感应极化的发生而改变，也就是说，一个电荷对另一个电荷的作用力的大小和方向，不因第三个电荷的存在而改变。
从本质上说，电荷是质量的固有极化状态，电荷作用是极化质量微粒间的相互作用。我们把电荷的空间称为该电荷的电场。所谓电场并不是真实存在的物质形态（它不能给处于其中的中性极化质量以任何电作用），它只是电荷相互作用与其空间关系的一种数学关系。电荷之间作用强度对其空间相对位置的相关性，证明了空间的客观实在性。
电荷之间的相互作用无需媒介，但并非超距的，电荷间的相互作用在真空中的传播速度为光速c；如果空间中存在介质，则电荷所受作用力除了与其空间位置有关，也与介质的极化状态相关。
孤立电荷的固有极化集度可以用电
来表示。在作用距离内的两个电荷，发生感应极化，感应极化的集度可以用相互作用力的大小来代表，符合库仑定律
3.电荷间的相对运动与磁作用力
3.1磁作用时参照系的特定性
我们已经知道运动电荷的磁感应强度公式是
磁场中运动电荷所受洛仑兹力为
我们来考察如下两个问题：
问题1：设A、B为两个带电粒子，对观察者的相对速度
，问AB间有无磁作用？
问题2：设A、B为两个带电粒子，对参照系Ⅰ的运动速度分
，对参照系Ⅱ的运动速度分别为
问AB间的磁作用力如何？
对于问题1，显然AB相对静止，如果按“静电荷”处理则AB间仅有库仑力，无磁力作用；如果按运动电荷A产生的磁场对运动电荷B的洛仑兹力计算，则有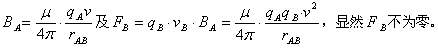
对于问题2，应用公式（1）及公式（2）将得到大小、甚至方向（如果其中一电荷对参照系Ⅰ、Ⅱ的速度方向相反）不同的结果。
显然，在问题1、2中，AB间磁作用力只能有一个确定的值，而不能用对任意参照系的相对速度来套用公式（1）及公式（2）。我们必须揭示相对速度 后面所掩盖着的绝对意义及磁作用力的本质。
3.2磁作用及磁力的产生
电荷之间的磁作用力的产生和大小只应与它们之间的相对运动有关。两个电荷对任意参照系的运动，最终归结为两个电荷间的相对运动。我们从两个电荷的相对运动入手来研究磁现象及磁力的产生。
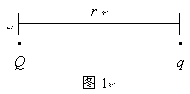
如图1所示，设有作用距离内的两个电荷
之间的感应集度用其作用力F来表示。
之间发生感应极化，极化集度（库仑力）为
象这种只改变感应集度的大小、不改变感应方向的作用，称为运动电荷间的电作用。
同样，不改变
之间的电作用的改变。
我们从能量角度对电荷间运动进行阐述。两个独立电荷在库仑力作用下运动时，两电荷组成的系统将产生动能，同时电荷的感应极化状态改变，电荷质量系统的内能（也即常说的电势能）减少，系统动能的增加等于其内能的减少。
的作用。
磁作用是客观存在的电荷间相对转动效应而非整体的空间转动效应，可用以下简单实验判定。
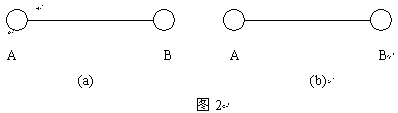
如图2所示，A、B为一绝缘连杆两端的两个带电金属球，其中B球刚性固定在连杆上，在A球的下部为一转轴，可用电机驱动旋转，测磁仪固定在转轴上方。在(a)中，A球及转轴均与连杆刚性固结，转轴可在轴套中转动，转轴转动时，转轴、连杆及A、B球均绕轴心转动；在(b)中，A球与转轴刚性固结，轴套固定在连杆上，转轴转动时，转轴及A球绕轴心转动而轴套及连杆保持不动。
磁作用理论断言：使转轴高速转动，在(a)中将不会测到磁场强度的变化，在(b)中将测到磁场强度的变化。使B球单独带电，仍有此结论。最一般地，在旋转的带电金属球外应测到由该带电体产生的磁场。
对于磁作用可以这样理解：当电荷孤立存在时，其固有极化方向是随机的，当两个相对静止的电荷相互作用时，其固有极化和感应极化将固定方向；当两个相对运动但距离保持不变（即相对转动）的电荷相互作用时时，其极化方向将发生相对于自身电荷质量微粒的转动，这就是磁作用。磁作用的表观效应就是磁力。
3.3运动电荷间磁作用力的大小
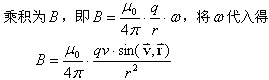
上式与式（1）的结果完全相同，这说明电荷对作用对象的磁感应强度B等于电荷感应强度与作用对象间相对转动的角速度的乘积。
上式即相对运动速度为
之间相互作用的磁力大小的计算公式（对其方向的讨论同经典理论，略去）。
我们对磁作用作进一步讨论：
1.磁场本质是强度不为零、方向变化的电场空间。磁作用由电荷间的相对转动产生，当电荷间的相对运动具有角速度（相对速度的切向方向分量不为零）时，电荷之间就产生磁作用。
2.在磁场中，如果电荷作沿磁力线方向外的任何运动，则该电荷将受到磁力的作用，反过来，该电荷也将对产生该磁场的电荷产生反作用。通电的直线螺旋管中的磁场是说明磁场的产生及对处于磁场中的运动电荷的作用的典型例证。
3.实验室中常用的磁场相当于由电荷的纯相对转动产生的“静磁场”，或者产生磁场的电荷的径向运动速度很小，近似于“静磁场”，故可以用相对于实验环境的相对速度来计算磁力的大小。
4.如果空间某处的磁场的强度或方向发生变化，则说明产生该磁场的电荷的数量或相对于该空间的运动速度发生了变化，相应地，对处于该空间的静电荷产生库仑力变化，即认为变化的磁场产生电场。
现在来看问题1、2，就非常简单易解了。
对于宏观磁力现象，可由式（3）或（4）进行计算。但需注意，对于载流导线之间的磁力作用，应取一根为“静”，将其中的流动电荷看作静电荷（因为导线中的电荷具有动态的连续性和稳定性，导线受力相当于动态“静”电荷所受洛仑兹力），然后求另一根导线中的运动电荷所产生的磁场对其作用的磁力。
4.磁作用理论的应用
在地球表面某处应用上式，即可分析计算地球磁场的形成和磁感应强度的大小和方向。
由磁力产生的必要条件可以解释超导现象及迈斯纳效应。
通常，导线中的电阻由两部分形成，一是原子及其电子系统的热运动，可称之为热电阻；二是导线电流磁场对导电电子的洛仑兹力作用，使电子的运动路线受到阻碍，形成电流磁场附加电阻（此电阻不带来能量损失），它比原子系统的热运动电阻大得多。
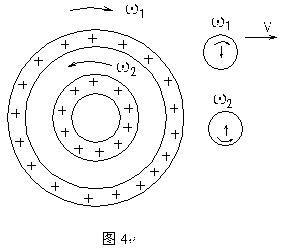
对那些超导材料来说，存在着这样的温度区间：在区间高限，原子的热运动仍不足以形成热电阻；在区间低限，材料中仍有足够密度的自由电子。在该温度区间内，初始起动电压使电子感应定向并立即达到较高的流动速度（可能远高于一般导体中的电子漂移速度）形成强大电流，电子靠惯性维持恒定的速度而形成稳流。由于回路中失去了电压，电子极化方向不受电源的感应定向而成为“拟自由电子”，而电子之间的感应定向是充分杂乱、均匀的，按照磁力的作用条件，在超导体内部就没有表观磁场。如果超导体处于外界磁场中，则超导电流中的外层电子被产生该磁场的电荷感应定向发生感应极化方向的偏转形成磁场，但该磁场与外磁场的方向相反，大小相等，表现出“抗磁效应”（如图3所示）。这样，在超导体内部的磁感应强度为零，这与导体的静电屏蔽效应相类似。这就是迈斯纳效应的根源。
以上关于超导现象的解释，比BCS理论中的“库伯对”的假设更合理。
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑