物理科学探疑-网友天空-相对论-对相对论的分析与批判
对相对论的分析与批判（上）
济南市花园路5号 王建华 著
文章提要：相对论是根据“相对性原理”和“光速不变原理”推导出来。本文根据迈克尔逊——莫雷实验，对相对论变换式推导过程进行了详细的分析研究。本文通过理论分析发现：爱因斯坦关于“相对性原理”的假设在理论上是错误的，而他对光速不变原理的理解和使用在理论上也是错误的。
本文由上、下两部分组成。文章上部对相对论的错误展开了理论分析和论述。文章下部对新的运动坐标变换式展开了理论分析和推导。
（由于本人能力有限，因此非常欢迎各位网友对我文章中的缺点错误提出批评指正。我的信箱是：wangjianhua850@yahoo.com.cn）
本文的理论分析和新的运动坐标变换式是以下面四个原理为基石展开的。
1、惯性系四维空间运动原理。
（1）所有惯性系的时空都是一个四维空间。每一个惯性系四维空间相对于另外一个惯性系四维空间来讲，只能拥有一个运动速度。
（2）如果K坐标系是惯性系，则相对于K系作匀速运动而无转动的其它K′ 坐标系也是惯性系。K′ 惯性系相对于K系作匀速运动，是指K′ 惯性系的四维空间相对于K惯性系的四维空间作匀速运动。
（3）相对于K惯性系的四维空间来讲，不同的K′ 惯性系四维空间拥有不同的运动速度。
（4）对于K系和K′ 系两个惯性系来讲，K惯性系中的任何一个时空点都同时对应着两个四维空间。其中一个是静止的K惯性系四维空间，而另外一个是运动的K′
惯性系四维空间。
2、自然定律的等效变换原理：
所有不同惯性系中的运动时空坐标，通过相同的运动坐标变换式都是能够进行等效变换的。即K系中的运动时空坐标与K′
系中的运动时空坐标，通过运动坐标变换式是能够进行等效变换的。自然定律在所有不同的惯性系中，通过运动坐标变换式等效变换后其作用规律都是一致的。
3、光子运动速度的极限原理：
对于所有的惯性系来讲，光子的速率都存在着一个最大的极限速度C。在任何一个惯性系中沿惯性系运动方向，观测同一运动方向的光子速率时，所观测到的光子速率V≤光速C。
4、绝对惯性系原理：
当我们自K惯性系四维空间中观测时，如果光子相对于K系空间一定点的速率V＝宇宙真空光速C，那么K系四维空间就是绝对静止惯性系。在绝对静止系中，光子的速率都等于宇宙真空中的极限光速C。而光子的速率C与光源在绝对静止系中的运动状态无关。
第一节、惯性系K与惯性系K′ 两者的运动时空坐标存在着线性变换关系。
（1）、K系运动坐标与K′
系运动坐标之间存在着线性变换关系。
设K坐标系和K′ 坐标系都是惯性系。假设O点和O′
点分别是K坐标系和K′ 坐标系的原点。假设K′ 系原点O′ 以速度U（U≠0）沿着正X轴线的方向运动，而质点P在K系中以速度V沿着X轴线运动。
假设自T＝ ＝0的时刻起，K系原点O，K′ 系原点O′ 与质点P这三者重合。当质点P沿着X轴运动到空间某一点P后。此时观测者自K系中观测，质点P在P点位置的时空坐标为（X、0、0、T）。与此同时，观测者自K′
系中观测，质点P在P点位置的时空坐标为（
、0、0、
）。此时K系坐标（X、0、0、T）点与K′ 系坐标（ 、0、0、
）点是空间的同一点。
特别需要指出的是：坐标（X、0、0、T）和（ 、0、0、
）两者在理论上应该具有两方面的含义。
其一、两者分别是K系和K′ 系中的几何空间长度和自然时间的流逝。
其二、两者分别是质点P在K系和K′ 系中的运动距离和运动时间。
对于我们的理论分析讨论来讲，坐标（X、0、0、T）与（ 、0、0、
）到原点O和O′ 的长度和时间指的是第二个含义。即指的是质点P在K系和K′
系两者中，从原点运动到空间P点后所具有的运动距离和运动时间。而不是指与运动无关的几何空间长度和自然流逝的时间。
所以我们应该把坐标（X、0、0、T）和（ 、0、0、
），称之为运动坐标。其中坐标X和 两者应该称之为质点P的运动距离，而坐标T和T′两者应该称之为质点P的运动时间。搞清楚这一点对下面的分析讨论是很重要的。
由于质点P在K系中的运动坐标（X、0、0、T）与质点P在K′
系中的运动坐标（ 、0、0、
）在数值上都具有唯一性，并且两者是同一个空间点，因此两个坐标之间的数量变换关系必定是一种线性的比例关系。
对于质点P在K′ 系中的运动坐标（ 、0、0、 ）来讲。当我们自K系观测时，质点P在K′
系中的运动距离应该是（X―UT）。而自K′ 系观测时，质点P的运动距离应该是
。
如果我们用β来表示K系与K′
系两者运动坐标之间的线性变换系数，那么自K系观测到的运动距离（X―UT），与自K′
系观测到的运动距离
，两者之间运动距离的线性变换关系式可以表示为：
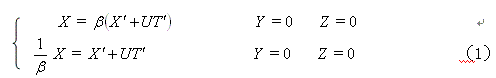
我们也可以利用解数学方程的方法得到上式。
在K系中决定质点P时空坐标大小的物理量有三个。其一是质点P在K系中的运动速度V，其二是质点P在K系中的运动时间T，其三是K′
系在K系中的运动速度U。从数学方程上讲，如果我们用 
来表示速度
对K′
系坐标的变换系数，用 
来表示速度
对K′ 系坐标的变换系数，用
来表示时间 T对K′ 系坐标的变换系数，那么K′
系坐标就可以表示成下面的形式。
而质点P在K′ 系中的运动速度
为。
由于速度V和速度U两者在K系中是性质相同的物理量，而两者只是在数量大小上有区别，因此变换系数
与变换系数
两者应该是同一个变换系数即 ＝ 。
当K′ 系在K系中的速度U＝0时，质点P在K系中的速度V与质点P在K′
系中的速度 
是完全相同的即 ＝ 
。由此可以确定：质点P速度V的变换系数 ＝1。于是变换系数 ＝ ＝1。于是上式可写成下面的形式。
由于K系与K′ 系两者是相对运动，因此K系在K′ 系中的运动速度也等于速度U，但其运动方向是相反的。如果我们通过把K′ 系中的运动距离进行变换改正的方式，来得到K系中的运动距离，那么我们就可以得到（1）式了。
应该指出的是：（1）式是K系和K′
系两者中的运动距离变换式，不是两者几何空间长度的坐标变换式。从这一点讲。不论运动距离是在X轴线上，还是在Y轴线上，变换系数
对于K系与K′
系两者中所有的运动距离来讲都是适用的。上式只不过是为了简化理论分析，而把质点P的空间运动距离放置在了X轴上而已。或者说，质点P在K系和K′
系两者中的运动距离此时只不过恰好与X轴重叠在一起而已。
（2）、相对性原理与数学运算法则相矛盾。
对于相对论来讲，它根据相对性原理把上面变换式表示成下面的形式了：
对于上面的相对论变换式来讲，由于 
和
都是K系中的运动距离，因此两者的变换系数在理论上就应该是完全相等的。对于K系中的运动距离来讲，它在相对论变换式中的变换系数是,而它在本文（1）变换式中的变换系数却是
。从这一点讲，相对论的变换式与本文的运动坐标变换式即（1）式，是完全不同的两个运动坐标变换式。
从数学四则运算法则上讲，当变换系数 ＝1时，相对论变换式是正确的。然而在变换系数 ≠1的情况下，相对论变换式在数学上是绝对错误的。因为把等式两边同乘以变换系数 后，根据数学运算法则是得不到相对论变换式的。
如果利用相对性原理强行使（2）式成立，那么要么变换系数 ＝1，要么在
≠1的情况下，所得到的变换式与数学运算法则相矛盾。遗憾的是相对论选择了后者。
相对性原理是爱因斯坦根据迈克尔逊——莫雷实验结果假设出来的。这一假设在理论上是否合理正确是非常令人怀疑的。
根据迈克尔逊——莫雷实验的光路示意图可知，光子在K′
系（地球）中来回所需要的时间
为。
上式就是利用经典物理学理论计算出的K′ 系运动时间与K系运动时间之差。经典物理学理论认为运动时间之差
≠0。然而迈克尔逊——莫雷实验的结果却证明：光子的运动时间之差
＝0。由于速度U≠0，因此根据迈克尔逊——莫雷实验结果可以确定，在K′
系（地球）运动时间
，与K系（宇宙真空）运动时间
之间存在着一个使时间差 ＝0的变换系数。
由于我们不论在什么地方，在什么方向上进行观测实验，但是最后所得到的实验结果始终是零，这一实验事实充分表明：K′
系运动坐标和K系运动坐标两者之间，无论在任何地方、在任何方向上，都存在着一个使光程时间差 ＝0成立的变换系数。没有任何一个地方，一个方向是例外的。这也说明了大自然的运动是和谐统一的。
如果根据相对性原理，那么由于光速C在任何坐标系中的速度都是相等的，因此速度U必然是等于零的，即U＝0。此时光子的运动时间之差
＝0。然而，爱因斯坦此时在理论上却犯了一个没有感觉到的错误，当我们根据相对性原理来解释迈克尔逊——莫雷实验时，那么光子在K′
系（地球）中来回所需要的时间 为。
由于 ＝t ，因此时间变换系数 ＝1。然而根据相对论变换式可知，此时变换系数 ＝0，或
等于无穷大。通过上面的分析可知，当爱因斯坦利用相对性原理来解释迈克尔逊——莫雷实验时，相对性原理本身就与相对论变换式是互相矛盾的。而且此时假设地球上的光速等于C也是错误的。
另外，我们在文章开始的时候，就曾经在理论上假设速度U≠0。而现在的天文观测也已经证明，K′ 系（地球）在K系（宇宙真空）中的速度U≠0。根据这两点可以确定，爱因斯坦根据迈克尔逊——莫雷实验结果所假设出来的相对性原理（该原理相当于任何惯性系的速度U都等于零）。无论在客观事实上还是在理论上都是错误的。
对于迈克尔逊——莫雷实验来讲，我们根据它的实验结果可以得到两个结论。
其一是由于地球速度U≠0，而实验结果等于零即 ＝0，因此K′
系运动坐标与K系运动坐标之间存在着一个使 ＝0的变换系数。
其二在不使用坐标变换式的情况下，我们仅仅通过实验本身是无法确定出地球相对于绝对静止系运动速度有多大。同时也无法证明光速在地球上的运动速度始终等于C。这一实验效应是双向的。不能只是用来说明无法确定出地球相对于绝对静止系运动速度有多大。
由于爱因斯坦在不使用坐标变换式的情况下，错误的假设了地球上的光速等于C，因此他关于相对性原理的定义在理论上必然是错误的。这就是为什么相对性原理与数学运算法则相互矛盾的原因所在。
第二节、对迈克尔逊——莫雷实验结果的理论分析。
对于迈克尔逊——莫雷实验来讲。如果我们把K系看成是静止惯性系，把地球看成是K′
惯性系，即地球在K系中的运动速度为U，把光子看成是质点P，即光子在K系中的运动速度为V＝C，那么（1）式中的坐标量
和
就应该是光子在K系中的运动距离（不能单纯的理解成仅仅是光子在X轴上的运动距离）。而两式中的坐标量, 
和 、
就是自地球上沿着地球运动方向观测到的光子在K′
系中的运动距离和运动时间。
（1）、在迈克尔逊——莫雷实验中，光子在K系和K′系两者中的运动时间。
根据干涉仪实验的光路示意图，我们可以得到光子在K系和K′
系两者中的运动时间。
在K′ 系中，光子从镜点 
点开始沿着 轴前去运动 
距离所需要的时间＝
。光子沿着
轴返回运动 距离到达镜点 所需要的时间=
。于是光子在K′
系中来回所需要的时间。
由于干涉仪在宇宙中的运动速度为U，因此光子在K系中就不能单纯地沿着Y轴上下运动。否则就会观测不到光子的运动。光子在K系实际上是以宇宙中的光速C沿着右上下方向运动的。
对于光子在K系（宇宙）中的运动距离来讲，当镜点
在K系中静止不动时，光子从镜点
开始沿着Y轴上或下的分速度为
。光子沿着Y轴上或下的运动距离都是
。于是光子在K系中上下运动所需要的时间。
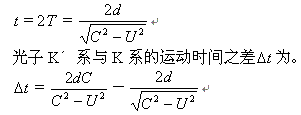
上式就是利用经典物理学理论计算出的K′ 系运动时间与K系运动时间之差。经典物理学理论认为运动时间之差
≠0。然而迈克尔逊——莫雷实验的结果却证明：光子的运动时间之差
＝0。
由于时间 是在K′ 系中得到的时间，而时间t 是在K系中得到的时间，如果假设K′
系运动时间的变换系数为
,或假设K系运动时间的变换系数为
,那么根据迈克尔逊——莫雷实验结果，我们可以得到下面两个关系式。
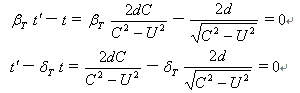
应该指出的是，上面两式中的速度U是K′ 系在K系中的运动速度，不是质点P的运动速度。然而在相对论变换式中，上式中的速度U却是质点P在K系中的运动速度。从这一点讲，上式中的变换系数 就不是相对论中的变换系数。
此时，上式中K′ 系运动时间的变换系数 与K系运动时间的变换系数
互为倒数关系。不是相等关系。即 ≠ 。
（2）、在迈克尔逊——莫雷实验中，光子在K系和K′系两者中的运动距离。
根据干涉仪实验的光路示意图，我们可以得到光子在K系和K′
系两者中的运动距离。
由于光子在K系中上下运动所需要的时间为，因此光子在K系中右上运动和右下运动的距离之和为
。
自K′ 系中观测时，光子从K系镜点 开始向前运动的距离为
自K′ 系中观测时，光子从K系镜点 开始返回运动的距离为
对于迈克尔逊——莫雷实验来讲，该实验就是想通过两个运动方向不同的光子，其中一个在K系做上下的运动，而另一个在K′
系沿着
轴做来回的水平运动。然后利用经典物理学理论计算出两个光子运动距离之差（即光程差），来确定地球在宇宙中的速度U。而上式中的光子运动距离之差
，就是迈克尔逊——莫雷实验用来确定地球运动速度U的光程差。经典物理学理论认为光子的K系与K′系的运动距离之差 ≠0。
然而迈克尔逊——莫雷实验的结果却证明：光子运动的时间之差 ＝0。这个实验结果表明经典物理学理论在高速情况下是错误的。
如果假设K′ 系运动距离的变换系数为 ，或假设K系运动时间的变换系数为
，那么根据迈克尔逊——莫雷实验结果，我们可以得到下面的关系式。
同样，上式中的速度U是K′ 系在K系中的运动速度，不是质点P的运动速度。上式中K′
系运动距离的变换系数与K系运动距离的变换系数
互为倒数关系。不是相等关系。即 ≠
。
上式变换系数 与 互为倒数。把上式代入（1）式后，根据（3）式，我们可以得到光子K′
系与K系之间运动距离的变换式。
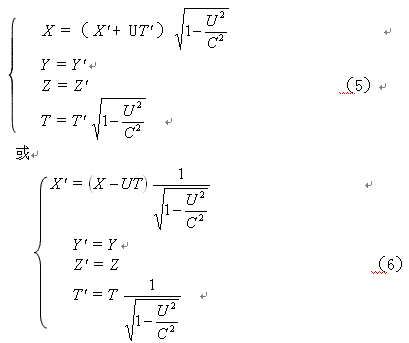
上面（5）式就是当K′ 系在K系中的速度为U时，把光子K′
系运动距离变换成K系运动距离的变换式。而（6）式则是把光子K系运动距离变换成K′
系运动距离的变换式。上面两个关系式在数学变换关系上，是完全符合数学运算法则要求的。从上面的两式可知，K′
系中的变换系数 与K系中的变换系数
，在理论上是完全不相等的，而者的变换系数互为倒数关系。
我们通过以上的分析可以确定，对于光子（仅仅对于光子质点来讲）在K′
系和K系中的运动距离来讲，相对论变换式实质上是一个错误的变换式。因为相对论变换式没有包括K′
系在K系中的速度U。如果令速度U＝光速C，那么迈克尔逊——莫雷实验中的运动时间差
和运动距离差 就不等于零了。即 ≠0。 ≠0。
需要指出的是：由于（5）式和（6）式的时间变换式中的不包含有运动距离 和
，因此光子的运动时间 
和 的大小与运动距离 和
两者的变化无关。这个结论与相对论的时空观点是完全不同的。
（3）、相对论变换式无法对迈克尔逊——莫雷实验结果做出合理的解释说明。
我们知道，相对论的变换式一般表示成下面的形式。
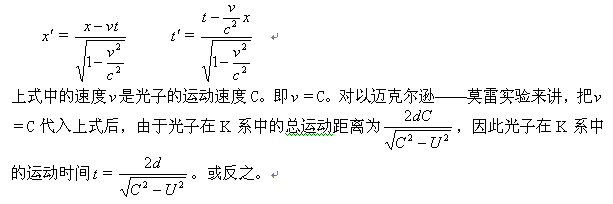
我们现在利用相对论仅仅得到了光子在K系中的运动时间t和运动距离
，而却无法得到光子在K′ 中的运动时间 和运动距离
。然而根据相对性原理，那么相对论变换式可以等效地变换成下面的形式。
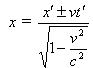
上式中取负号是光子前往的变换式，取正号是光子返回的变换式。根据相对论的光速不变原理，光子在K′
系和K系中的速度都是C。对以迈克尔逊——莫雷实验来讲，把 
＝C代入上式后，由于光子在K′
系中前往和返回的运动距离都是 ，因此光子在K′
系中前往和返回的运动时间都等于
。即=。
然而，由于目前的天文观测已经证明，地球在宇宙中的速度U≠0，因此光子在迈克尔逊——莫雷实验中，前往的运动时间=
，返回的运动时间
=。可见光子在迈克尔逊——莫雷实验中前往运动时间和返回运动时间是不相等的。迈克尔逊——莫雷实验也正是由此来计算确定干涉条纹会移动的，而不是根据光子在K′
系中前往和返回的运动时间都等于，来计算确定干涉条纹会移动的。
根据以上的分析讨论可以确定：当地球在宇宙中的速度U≠0时，利用相对论变换式是无法对迈克尔逊——莫雷实验结果进行解释说明的。
第三节、相对论变换式在理论上是错误的。
（1）、相对论在理论上是错误的。
对于相对论变换式来讲，自K′ 坐标系观测时，当运动距离变换变换系数为K′ 时，那么运动距离变换式为：
而自坐标系K观测时，当运动距离变换变换系数为K时，那么运动距离变换式为：
误的。
（2）、相对论坐标变换式与迈克尔逊——莫雷实验之间存在着严重的矛盾。
相对论的运动距离和运动时间的变换式为。
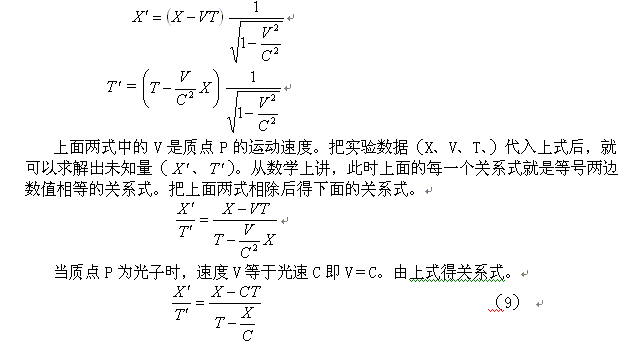
如果我们把X和T看成光子在K系中去的运动路程和去的运动时间，那么根据迈克尔逊——莫雷实验可以得到关系式。
由上面可以得到关系式X―CT＝0。把该式和（9）式代入（10）式可以得到下面的关系式。
上式等号两边的数值就是（9）式等号两边的数值。这一结果首先在数学上就是极端错误的，因为任何两个等式相除后所得到的新关系式仍然是等式。而上式结果却表明（9）式不是一个等式关系。
其次，由于速度U是K′ 系（地球）在K系（宇宙真空）中的运动速度，不是光速，因此光子在宇宙中的运动速度C等于地球在宇宙中的运动速度U，这个结论显然也是绝对错误的。
由此可以确定：相对论变换式与迈克尔逊——莫雷实验结果存在着严重的矛盾。或者说，利用相对论变换式是无法对迈克尔逊——莫雷实验结果进行解释说明的。
(3)、相对论变换式是一个偷换速度概念的变换式。
物理学家推导洛仑兹运动距离和运动时间变换式的过程如下：
由于相对论变换式是利用错误的原理和错误的方法推导出来的，因此它在理论上是错误的。
综合以上的理论分析可以确定：相对论变换式在理论上的错误如下：
7、与迈克尔逊——莫雷实验结果存在着严重的矛盾。因为任何两个等式相除后所得到的新关系式仍然是等式。而利用相对论变换式所得到的（8）式两边却不相等。
王建华2003年1月6日于济南
我的信箱是：wangjianhua850@yahoo.com.cn
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑