物理科学探疑-网友天空-相对论-Newton-Einstein经典统一力学纲要
![]()
Newton-Einstein经典统一力学纲要
(线性部分)
李晓刚
邮编:710082 地址:陕西西安新园路二号 西电软件中心
电话:029-8636867 13572872399 电邮:lxg6226@sina.com
摘 要 以广义复几何为新型手段,把Newton力学和Einstein相对论力学统一在一个数学模型之中,铸就成所谓的“Newton-Einstein经典统一力学”。
关键词 Galileo抛物几何, Minkowski双曲几何, 广义复几何, Galileo-Lorentz四维广义复时-空统一变换, 度量空间弯曲程度的运动学和动力学曲率。
序言
早在二十世纪初,人们就已经对Einstein相对论力学和Newton力学的数学结构做了最透彻的研究。其研究后果之一就是把Newton力学与Galileo抛物几何空间[1]相对应;把Einstein相对论力学与Minkowski双曲几何空间[2]相对应;直言之,Galileo惯性运动变换群确定了Newton力学空间为非Euclid性质的Galileo抛物空间;而Lorentz惯性运动变换群确定了Einstein相对论力学空间为非Euclid性质的Minkowski双曲空间。
最令人惊讶不已的是,远在古希腊科学初创时期,人们就尝试把整个宇宙空间假设为三维Euclid空间(也不乏有人尝试把其假设成球面空间)。可是近代科学的发展后果表明,古希腊人所期望的至少到今天,还未能得到近代科学的证实,相反,Einstein相对论力学和Einstein引力场论的举世公认,诱导人们将自然界空间约定成四维的非Euclid性质的空间;Newton力学无比简洁的深远影响,很自然地促使人们把自然空间倾向于约定成最简单的四维的Galileo空间。是否我们的宇宙就是偏爱这种人心约定的四维的非Euclid性质的空间呢?这是一个耐人寻味的问题。
有趣的是,Galileo空间在诸多类型的空间中,相比之下竟是已知最简单的空间,虽然长期以来在一般人的印象中总是以为Euclid空间是比非Euclid空间更为简单的空间。实际上Euclid空间却是比Galileo空间更为复杂的空间。如果按Mach博士关于自然界总是偏爱他所称的“经济思维原则”进行之说,这种非Euclid的Galileo空间无疑是宇宙首选的理想空间。
到了二十世纪中叶,广义复几何学[3] (包括广义三角函数理论)这种统一几何学已创初形,这是个别守旧的而不赶时髦的老欧洲数学家伟大劳作的后果。或许他们是自觉地沿“自然界总是按数学法则行事”这一科学初创时期的假设出发的数学家,长期以来默默地致力于物理学的公理化研究。他们的优秀工作,使得我们在今天在此基础上稍加创造就能够以广义复几何为工具,把Newton力学和Einstein相对论力学统一起来,铸就成所谓的“Newton-Einstein统一力学”,这一切不可不谓是“水到渠成”。
众所周知,人们往往在二维空间中来描述弯曲的线,在三维空间中描述弯曲的面。自然,在四维空间中描述弯曲的空间。其Einstein相对论力学就是在四维空间中描述的。为了完成我们所称的“Newton-Einstein统一力学”——这一前所未有的课题,自然需要把Newton力学也嵌入四维空间中,对人们熟知的Newton力学重新给予完整的物理性的数学描述,使之和Einstein相对论力学的“四维数学模型”不仅同构而且同形。
不仅如此,还需要选择四维广义复数空间模型,采用同一个“广义复时-空惯性运动变换群”重新描述“Newton-Einstein统一力学”的全部基本内容。要想实现这种经典物理学的统一,选择广义复几何空间模型作为物理学的新工具则是必不可少的,已知这是目前实现二者统一的唯一选择。也许,它是Felix
Klein教授的Erlangen program精神首次在经典统一物理学的具体实践。
换言之,我们要给Newton力学和Einstein相对论力学编织款式完全相同的一套崭新时装——用同一种数学模型去描写两种不同的物理模型——Newton力学和Einstein相对论力学。即选择四维广义复几何空间来描写所谓的“经典统一力学(线性部分)”,重新审视Newton力学和Einstein相对论力学全部核心内容,确立一种全新的统一的四维广义复时-空的观点及其研究方法。
在这种“Newton-Einstein统一力学”的理论框架中,存在一种优越的广义复惯性系,在Galileo-Lorentz四维广义复时-空变换下,不仅Newton力学是对的,Galileo变换是适用的,而且Maxwell电动力学也是正确的,Lorentz变换同样也是成立的。直言之,对于这种新的经典统一物理学来说,存在一个既适用于Newton力学又适用于Maxwell电动力学的广义复相对性原理。继而从根本上克服旧经典物理学内在的Galileo变换群和Lorentz变换群的逻辑不统一性,包括Newton力学与Maxwell电动力学的内在不统一性,以及Newton力学和Einstein相对论力学的内在不统一性。不禁要问,难道真的如Poincaré所说的那样:“一切都不过是人心的自由约定” ?
1、 四维时-空惯性运动变换群
人们总是喜欢选择最简单的假设,以求用最简洁的数学形式来凸显物理的本质。这种思行观是由来已久的最深入人心的优秀传统之一,Mach称之为“经济思维原则”。这无疑也是笔者所喜用的原则。
由于每一种空间类型总存在与之相伴的对偶空间,无不成双成对。故而我们仅当且只从物理学的角度才使用“协变性”这一专门名词。极力避免和纯粹数学上的“协变性”一词相混淆。否则有可能重蹈Einstein在引力场论上的覆辙——非常不幸地将这种毫无半点相对论气息的理论错误地称作“广义相对论”。这是因为物理学的“协变性”和纯粹数学上“协变性”在内涵上风马牛不相及——实在是相差甚远,不可同日而语。如果不是因为有着深刻的历史根源,我们完全有理由给这些概念以不同的名称。物理学的“协变性”在没有被任何误解和扩大的前提下,乃是特指“在至少两个标度完全相同的参照系相对匀速、或加速、或作用力、或力偶变换下物理方程式或物理量保持不变的性质”。而纯粹数学上“协变性”在没有被任何误解和扩大的前提下,则是指任一方程式或某量在每一种空间类型中和总存在与之相伴的对偶空间相对变换中自动保持不变的性质。所以本文刻意既不随大流去使用“协变矢量”和“逆变矢量”这两个名词,也决不滥用“协变性”这一专门名词。
我们约定“协变矢量”就是列矢量|xμ>;“逆变矢量”就是行矢量<xv|。一开始就处处广泛使用量子力学的Dirac算符,努力做到开卷有益。
沿袭Mach称之为“经济思维的原则”,我们假设:原先两个时-空标度相同、时-空原点重合、对应的各坐标轴彼此始终平行的四维参照系K`(![]() )和K(
)和K(![]() ),K`相对K以速度 沿K的
轴向作匀速直线运动,并且0≤ν <c(c——光速)。(这种特殊假设不是必需的,两个坐标系原点也不必重合,对应的各坐标轴彼此始终可以保持不变的固定角度,K`相对K以速度
ν可沿任一方向匀速直线运动。)对任—质点P的四维正时-空描述:
),K`相对K以速度 沿K的
轴向作匀速直线运动,并且0≤ν <c(c——光速)。(这种特殊假设不是必需的,两个坐标系原点也不必重合,对应的各坐标轴彼此始终可以保持不变的固定角度,K`相对K以速度
ν可沿任一方向匀速直线运动。)对任—质点P的四维正时-空描述:
在K`中,为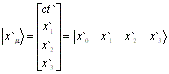
在K中,为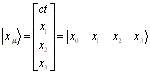
对同—质点P的四维对偶的倒易时-空描述:
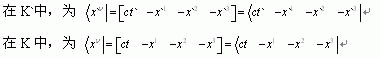
以上各式中引进真空光速c这一绝对不变量,保持四维时-空坐标具有一致相同的统一量纲,则是为了使变换群作用算子能够像其它算子一样不含任何物理量纲。
一个四维时-空矢量的正易列矢量分量和其对偶的倒易行矢量分量的关系,可以用下式表达:
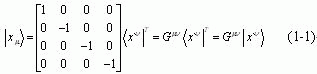
限于篇幅,与之“对偶的Galileo四维倒易时-空变换”、“对偶的Lorentz四维倒易时-空变换”和“对偶的Galileo-Lorentz四维广义复倒易时-空”变换均是数学协变性的产物,它们对物理实质无任何贡献而没有必要一一列出,在以后的讨论中如无必要均不再明显陈述。
如无特别申明,下述内容均按以上约定。
2、Galileo四维时-空惯性运动变换
假如,对同一事件两个四维时-空惯性系K和K`的时钟同步。按Galileo观点,可知关于P点的时-空坐标变换有如下关系:
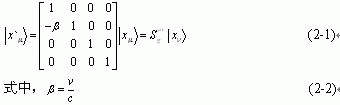
由 (2-1) 式所确定的变换,就叫Galileo惯性运动变换,它又被称作Galileo相对性原理。
凡是在变换 (2-1) 式下,保持不变的物理公式或物理量,就被称作Galileo绝对式或绝对量。只有这一类物理公式或物理量在Newton力学中才有实际意义,才会成为被研究的物理学对象。
Galileo惯性运动变换群:![]()
从数学上来说,整个Newton力学(不包括非惯性运动部分)就是关于Galileo变换群的不变式的理论。
由Galileo惯性运动变换群所确定的四维几何空间,就叫Galileo四维几何学。它是八十一种Felix
Klein四维几何学中相对唯一最简单的几何学,远比四维Euclid几何简单得多!
需要特别指出的是,在Galileo四维几何学中,人们熟知的加速度其实就是四维惯性运动空间的曲率——它是度量四维惯性运动空间弯曲的程度的物理量。匀加速度是正曲率,而匀减速度是负曲率。而人们熟知的Newton作用合力则是四维动力学惯性空间的力学合曲率——它是度量四维动力学惯性空间总弯曲的程度的物理量。
类似地,各种非惯性运动的加速度就是非惯性运动的场强,它是度量非惯性运动场空间的曲率——一个标度非惯性运动场空间弯曲大小的物理量。各种非惯性力都是非惯性场力,均是度量非惯性力场空间的曲率——一个标度非惯性力场空间弯曲大小的物理量。
显而易见的是,各种倒易的加速度就是度量四维运动学空间弯曲的半径。各种倒易的作用力则是度量四维动力学空间弯曲的半径。
同样,人们耳熟能详的引力场的场强,其实就是引力场强空间的负曲率,它的大小确定了引力场强空间弯曲的程度。以地球引力场强空间弯曲的程度为例,其地表的引力场强空间弯曲程度最大!从地心延伸到地表,地球的引力场强空间的弯曲程度是在均匀地线性缓慢递增(正曲率);由地表向太空延伸,其地球的引力场强空间的弯曲程度则是在非均匀地非线性迅速递减(负曲率)。由于地球内部物质质量和成分分布的不均匀性,所谓“自由真空垂直下落的物体”并非沿数学几何上的铅垂线下落,而是沿地球的引力场强空间最大弯曲的方向下落。
地球和太阳的引力大小则是太阳和地球的合引力场空间的弯曲程度的度量。由于太阳巨大质量使得整个太阳系的合引力场空间的弯曲程度在数量级上近似等于太阳单独引力场强空间的弯曲程度。所以,可以认为地球沿太阳引力场负曲率的弯曲空间中运行。和Einstein的“广义相对论”正曲率的宇宙模型恰好相反——在现实世界中任何物质的真实引力场空间一律都是负曲率性质——因为任何两个物体的相互作用的万有引力永远是负的! 有趣的是,对于任何一个球形的星体来说,其物理学上的负曲率模型竟然和其数学几何上的正曲率模型正好完全相反。这是Galileo景绘。物理学每每表现出的这种和人的直觉恰好相反的生动实例再次提醒人们——古希腊人本主义所谓的“人是万物的尺度”是错误的,人的直觉往往是危险的,宇宙自然万物从来也不是按照我们人类的直觉来构造的,当然人造品除外。“以人为本”的理念至少在自然科学领域向来无效。
自然,其Newton作用力的数学本义,即动力学空间的内切空间曲率。即便可观察的表象的质点或物体保持相对静止状态,或者其几何运动路径是直线形式,这种动力学曲率依然存在。它的大小和存在性和纯粹数学根植在人们脑海中通常的曲率概念竟然如此不同,然而它始终却是度量动力学空间弯曲程度的物理量。比如,一个垂直自由运动的落体或一个保持平衡的静止物体的重力均可反映出引力空间曲率的大小,也就是说万有引力的大小和方向就是万有引力空间曲率大小和方向的度量。可以这么说,Newton第二定律在Galileo惯性运动变换下的不变性,本质上是“动力学空间的曲率” 在惯性运动下的绝对不变性的真实体现而已。所以Galileo相对性原理又可以表述为,我们不能借助任何判定动力学空间的曲率的大小和存在性的物理实验,来判定所在的参照系的状态究竟是处于静止的还是匀速直线运动的。
广而言之,对于任一质点,不单单Newton作用力是动力学空间的曲率,所有其他任何类型的作用力(比如,摩擦力、弹性力、电力、磁力、非惯性力、广义力、电磁力、弱力、强力等等) 。一律都是在四维空间中描述动力学空间弯曲程度的曲率(而其中的摩擦力则是动力学负曲率,在四维空间中它做的是负功)。数学中的曲率一般是标量,而物理学中的曲率一般是矢量,它的模是标量。当然,数学和物理学的曲率还可以是张量,限于主题不在此阐述。重要的是物理学中的作用力扮演了动力学空间曲率的角色!这使我们对作用力或曲率这两个极其关键的核心概念有了重新的深刻认识和理解,这无疑是Galileo几何学对物理学最直接的显赫贡献之一。
通常所谓的“惯性运动”其实就是运动空间曲率处处为零的运动;惯性参照系本质上就是空间曲率处处为零的参照系——即所谓空间平坦的参照系。
相应的任一非惯性参照系,其实质原来也就是空间曲率均不为零的参照系而已。
至此,我们已经给出了参照系的严格定义。从定义出发,我们更能深刻地认识和理解到:局部均匀真空电磁场则是目前已经发现的唯一的自然惯性场,它是最好的自然惯性参照系。宇宙平均电磁场也可以被认为是一个相对良好的永久准惯性参照系。至于相对地球遥远的可观测的恒星或星系算是比较好的短期伪惯性参照系。当然,对于沿地球引力等势面上做短距离物体运动来说,在许多情况下地球也可以被认为是一个相对很好的局部准惯性参照系。诚然,除了局部均匀真空电磁场和宇宙平均电磁场外我们再也没有发现严格意义上的任何真实惯性参照系。
由于真空中的光速永恒不变,这意味着我们人类所处的这个宇宙真空空间内切曲率竟然为零![]() 相对常观的各种运动学曲率的绝对值来说它就是最小的了,直接地表明我们星球所处的宇宙的真空空间始终就不曾存在最后的边界,其广袤深远的浩瀚的宇宙真空空间半径是恒为无穷大——其零曲率状态永世不变!
相对常观的各种运动学曲率的绝对值来说它就是最小的了,直接地表明我们星球所处的宇宙的真空空间始终就不曾存在最后的边界,其广袤深远的浩瀚的宇宙真空空间半径是恒为无穷大——其零曲率状态永世不变!
另一方面,我们已知人类所处的这个宇宙真空引力空间内切曲率竟然为一永久物理常数![]() 相对常观的各种动力学曲率它可能是最大的——假如真空中的光速是最大的话。对于任何大小的引力而言,总是
相对常观的各种动力学曲率它可能是最大的——假如真空中的光速是最大的话。对于任何大小的引力而言,总是![]() 。这意味着无限深远的宇宙中的任何一个星系的引力的作用空间范围都是有确定无疑的最后边界的
。这意味着无限深远的宇宙中的任何一个星系的引力的作用空间范围都是有确定无疑的最后边界的![]() ,其引力的作用空间范围从来也不是真正无限的。星系之间的相对红移现象本身从另外一个角度表明了它们之间不再被引力所束缚。
,其引力的作用空间范围从来也不是真正无限的。星系之间的相对红移现象本身从另外一个角度表明了它们之间不再被引力所束缚。![]() 这一物理学结论不仅直接永久性地彻底否决了人们曾经关于总星系的假说!同时也给出了关于星系之间相对红移的一种非宇宙大爆炸所致的崭新的理论诠释。
这一物理学结论不仅直接永久性地彻底否决了人们曾经关于总星系的假说!同时也给出了关于星系之间相对红移的一种非宇宙大爆炸所致的崭新的理论诠释。
而这一切,不但已经远远超越了我们人类现有已知的科学知识的最后边界,而且也远远超越了我们人类现有已知的哲学和宗教学知识的最后边界。这显然是Galileo几何学对物理学,乃至对整个人类古往今来的全部知识库最伟大的贡献之一
3、Lorentz四维时-空惯性运动变换
假如,对同一事件两个四维时-空惯性系K和K`中的光速相同,按Einstein观点,可知关于P点的时-空坐标变换则有:
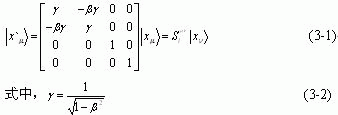
由 (3-1) 式所确定的变换,就叫Poincaré-Lorentz惯性运动变换,它又被称作Einstein相对性原理。
凡是在变换 (3-1) 式下,保持不变的物理公式或物理量,就被称作Poincaré-Lorentz绝对式或绝对量。只有这一类物理公式或物理量在Maxwell电动力学和Einstein相对论力学中才有实际意义。
Poincaré-Lorentz变换群: ![]()
从数学上来说,Einstein相对论力学就是Poincaré-Lorentz惯性运动变换群的不变式的理论。
由Poincaré-Lorentz惯性运动变换群所确定的四维几何空间,就叫Minkowski四维几何学。
正是均匀电磁场空间的曲率处处为零,对同一事件两个相对匀速直线运动的四维时-空惯性系K和K`的光速才会表现出唯一恒定性而不发生任何改变。反过来说,如果这两个惯性参照系中的光速完全相等,则表明它们二者均处于运动学曲率处处为零的均匀电磁场空间之中。继而容易推断出:对描述同一事件两个相对匀速直线运动的四维时-空惯性系,假如都是处于运动学曲率并非处处为零的非均匀电磁场空间之中,即使没有引力场的任何影响或影响完全等同的条件下,二者各自对同一光信号所测得的速度未必一致。这就勾画出了Lorentz惯性运动变换的适用或者说不再成立的大致范围了,这就说只有当Maxwell电动力学处于运动学曲率处处为零的均匀电磁场空间之中才能严格成立。当然,现存量子力学、量子电动力学等等其它诸多学科的适用范围也同样如此。在现实世界里,许多情况下其实测的均匀电磁场空间或宇宙平均电磁场曲率处处为零至多是一个近似的或平均统计的后果。现在人们容易理解为什么当初Einstein试图将Lorentz惯性运动变换推广至引力场时会不幸地遭到了彻底的失败。
那是因为引力场空间运动学的曲率除了中心点为零之是处处不等的变曲率的空间。相形之下,均匀电磁场空间的运动学曲率则是处处为零的常曲率的空间。因此二者所确定的空间性状尖锐相冲突。所以Einstein的失败那是必然的。重要的是Einstein第一个为我们后继者揭示了电磁场和引力场深刻的渊源,并留下了使后来者足以深究的基本线索。
如果我们在非线性统一力学中,应用其非惯性加速变换群或非惯性作用力变换群就能够描写Newton引力场空间,Newton非惯性运动空间,非均匀的曲率处处不为零的非线性电磁场空间,以及非均匀的曲率处处不为零的非线性量子场空间。从而在Einstein失败的地方重新站立起来。限于本文的主题,不再赘述。
4、Galileo-Lorentz四维广义复时-空统一惯性运动变换
假设:原先两个时-空标度相同、时-空原点重合、对应的各坐标轴彼此始终平行的复四维参照系![]() 和
和![]() 相对 以速度 沿 的
轴向作匀速直线运动,并且0≤ <c(c——光速)
相对 以速度 沿 的
轴向作匀速直线运动,并且0≤ <c(c——光速)
对任—质点P的四维广义正变复时-空描述:
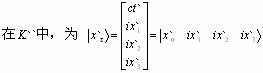
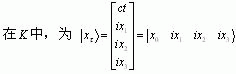
从以上的描述可知:广义复时-空的确切含义是“实时-广义虚空”。
其中,广义复数的类型和角的测度:

对广义复数而言,

广义复数的类型和广义三角函数:
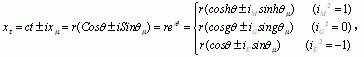
广义三角函数系指:![]()
广义复数的类型对应的部分几何门类:
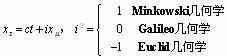
而广义复数的类型对应的力学门类:
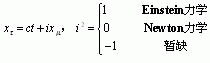
对同—质点P的四维对偶的倒易时-空描述:
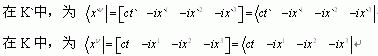
类似地,以上各式中引进光速c这一绝对不变量,也是为了保持四维广义复时-空变换群作用算子能够像其它算子一样不含任何物理量纲。
需要特别指出的是,这种“实时间-广义虚空间”![]() 的定义乃是统一物理学理论本身逻辑结构内定的,也是唯一的,不能由人心自由任意约定。并且,在物理学上不存在与之相对偶的“广义虚时间-实空间”
的定义乃是统一物理学理论本身逻辑结构内定的,也是唯一的,不能由人心自由任意约定。并且,在物理学上不存在与之相对偶的“广义虚时间-实空间”![]() 尽管在纯粹数学上并无此限制。广而言之,数学在任何条件下都可说:“我思故我在”(Descartes语);而物理学则不论在什么条件下至多可说:“我在故我思”。
尽管在纯粹数学上并无此限制。广而言之,数学在任何条件下都可说:“我思故我在”(Descartes语);而物理学则不论在什么条件下至多可说:“我在故我思”。
按“Newton-Einstein统一力学”观点,考察Galileo四维时-空惯性运动变换(2-1) 式和Lorentz四维时-空惯性运动变换(3-1) 式,并结合广义复数理论,那么关于P点的四维广义复时-空统一坐标变换则有如下统一关系:
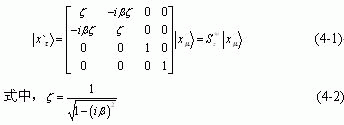
由 (4-1) 式所确定的变换,就叫广义复时-空统一惯性运动坐标变换,它又被称作广义复时-空统一相对性原理,也可称作为“线性广义统一相对性原理”。
凡是在变换 (4-1) 式下,保持不变的物理公式或物理量,就被称作广义复时-空统一变换下的绝对式或绝对量。
不论是Newton力学![]() 还是Maxwell电动力学
还是Maxwell电动力学![]() 或波动方程
或波动方程![]() 在统一变换 (4-1)
式下均保持各自的协变性。
在统一变换 (4-1)
式下均保持各自的协变性。
广义复时-空统一变换群:![]()
从数学上来说,全部经典力学(线性部分)就是关于广义复时-空统一惯性运动变换群 (4-3) 式的不变式的理论。
这种由广义复时-空统一惯性运动变换群所确定的四维几何空间,就叫广义复时-空统一四维几何学。
至此,由 (2-1)、(3-1)、(4-1)
三式,我们可以得到下面的结论:
| 变 换 | Galileo | Lorentz | Galileo-Lorentz |
| 经典质点力学定律 | 形式不变 | 形式变 | 形式不变 |
| 经典波动力学定律 | 形式变 | 形式不变 | 形式不变 |
| 经典电动力学定律 | 形式变 | 形式不变 | 形式不变 |
所以以我们说,广义复时-空统一惯性运动变换群能够彻底统一描述局域的经典粒子力学和描述全域的经典波动力学。
5、Galileo-Lorentz四维广义复时-空的统一数学结构
统一性思想乃是印入人类心灵深处中的一种最古老的宗教信念之一。这种万流归一的思想在这里,它至少包含这样的四重意思:一是揭示物理运动的内在统一性,使物理学理论与所描述的理想模型相统一;二是揭示物理学内部的逻辑结构具有一致性,使同一理论不同部分相互协调,呈现出自然发展的序列性和整体的系统性;三是揭示物理学和研究对象的简单性,最大限度地表述了物理学普遍规律的最简洁的形式,使得物理学理论结构紧凑,层次分明,系统和谐。从而满足物理学和研究对象的直觉简单性和数学简单性;四是揭示物理学统一变换下的绝对不变的对称性思想,而这种不可分辨的同一的对称性和绝对不变性不仅是其物理学和其研究对象最本质特征的反映,而且它还严格规定了时-空的几何最基本的结构,以及严格限定了物理学基本定律与核心物理量的种类和数量。
在Newton-Einstein统一力学中, 四维广义复时-空的间隔
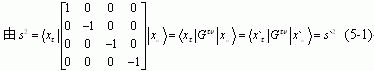
的不变性得到四维广义复时-空的Galileo-Lorentz统一变换。
我们可以按保持 不变的一切变换的群来考虑,这个群就是所谓的“齐次Galileo-Lorentz统一变换群”。它包括普通转动和 (4-1) Galileo-Lorentz统一变换。
而保持![]()
不变的一切变换的群是所谓的“非齐次Galileo-Lorentz统一变换群”。它包括时-空的隔距和反射,以及 (4-1) Galileo-Lorentz广义复时-空统一变换。这里仅限于讨论齐次Galileo-Lorentz统一变换群,简要地阐述模方由 (5-1) 式确定的广义复时-空的数学结构。
在非Euclid性质的Galileo-Lorentz广义复时-空空间中,倒易时-空连续统是用坐标为
![]() 的四维空间来定义的。其变换是按照
的四维空间来定义的。其变换是按照
![]()
得到新坐标![]() 的变换。
的变换。
与其 (5-1) 式对偶的保持模方不变的可表述为:
![]()
根据 (5-3) 式我们来求坐标的线性变换群
![]()
把 (5-5) 式代入 (5-4) 式得
![]()
由 ( 5-6) 式可知
![]()
对 (5-7) 式两边取行列式得
![]()
于是, ![]()
关于广义复变换群元![]() 的性质:
的性质:
![]() 相当于连续施以恒等变换——正常的Galileo-Lorentz变换。
相当于连续施以恒等变换——正常的Galileo-Lorentz变换。
![]() 是非正常的Galileo-Lorentz变换。
是非正常的Galileo-Lorentz变换。
由于广义复时-空度规的不定性,这两种Galileo-Lorentz变换不能用![]() 来明确区分。比如,
来明确区分。比如,![]() (空间反演),这时
(空间反演),这时![]()
![]() (时间和空间反演),这时
(时间和空间反演),这时![]() 。以后我们只考虑正常的广义复Galileo-Lorentz变换。
。以后我们只考虑正常的广义复Galileo-Lorentz变换。
广义复变换群元
的第二个性质:是完全确定一个变换所需要的参数的数目。由 (5-7)
式知它是 对称矩阵,因此![]() 的16个元素只有10个是独立的。
的16个元素只有10个是独立的。
为了求出![]() 的结构
的结构
假设 ![]()
![]() 是
是 ![]() 矩阵。对 (5-10)
式两边取行列式,结合 (5-9) 式并按约定,
矩阵。对 (5-10)
式两边取行列式,结合 (5-9) 式并按约定,
![]() 是一个迹为零的矩阵。
是一个迹为零的矩阵。
( 5-7) 式又可以写作![]()
结合(1-3) 、(5-10)、 (5-11) 三式,可得
![]()
连解 (5-11)、(5-12) 式可得
![]()
于是, ![]() 一般形式为
一般形式为
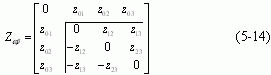
(5-14) 式及其6个参数是变换群元![]() 的一种明确结构。为了显现这个结构的物理含义,通常引进两组初等矩阵。一组显现两个广义复参照系的相对速度,
的一种明确结构。为了显现这个结构的物理含义,通常引进两组初等矩阵。一组显现两个广义复参照系的相对速度,
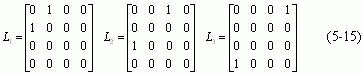
另一组显现两个广义复参照系坐标轴的相对取向,
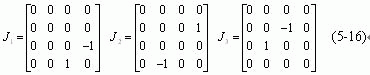
![]()
这两组的初等矩阵的平方都为对角阵:
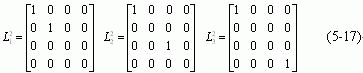
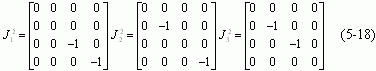
于是,![]() 一般形式(5-14)式可写成另外一种形式:
一般形式(5-14)式可写成另外一种形式:
![]()
结合以上结论,![]() 的一般形式(5-10)式能表述为:
的一般形式(5-10)式能表述为:
![]()
如果令![]() 结合(5-15)- (5-19)诸式,可得
结合(5-15)- (5-19)诸式,可得
![]()
其显式为
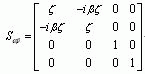
对于沿任意一个方向的纯平动而言,
![]()
![]()
![]()
于是,纯平动为
![]()
其显式为
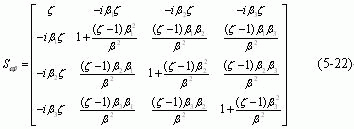
(5-22)式的六个矩阵是无穷小生成元的一种表示。计算可证,它们满足下列对易关系:

第一个关系表明,平动矩阵是不对易的,特征负号表明的四维广义复时-空变换群代数结构![]()
第二个关系表明,转动矩阵是对易的。
第三个关系表明, 在转动下按一个矢量变换。
总之,Galileo-Lorentz四维广义复时-空变换群具有不对易性的运动学结果。
参 考 文 献
[l] Galileo几何
H. Beek 最小曲面的几何学,Sitzungsber. Leipziger Berliner Math. Gee.12:14-30,1913
L. Silberstein, Galileo时空中的射影几何 ,Philos. Mag. 10: 1925
Makarova, N., M., Tow-dimensional Noneuclidean Geometry with Parabolic Angle and
Dissertation, Leningrad, 1962
[2]Minkowski几何
A. Einstein关于相对性原理和有此得出的结论 爱因斯坦文集 第二卷
商务印书馆出版,1977
J. D. Jackson, Classical Electrodynamics. John Wiley & Sons Books Lnc. 1975
Shervatov, V. G.., Hyperbolic Functions. Heath, Boston,1963
[3]广义复几何
Schwerdtfeger, H., Geometry of Complex Numbers. University of Toronto Press, Toronto 1956
Deaux, R., Introduction to the Geometry of Complex Numbers. Ungar, New York 1956
Newton-Einstein Classical Unified Mechanics Program
Xiaogang Li
Address:XD Software Center,The Number 2 of New Park Road,XI`AN,SHANNXI,
Post:710082 Tel:029-8636867,Mobile Tel:13572872399 Email:lxg6226@sina.com
Abstract Newtonian mechanics and Einsteinian theory of relativity mechanics are unified,
and Newton-Einstein Classical Unified Mechanics is founded in general
geometry of Complex Numbers.
Keywords Galileo parabolic geometry,Minkowski hyperbolic geometry,General geometry of
Complex Numbers,General Galileo-Lorentz four-dimension complex
space-real time unified transformation, Compound curvature of Kinematics or Dynamics
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑