物理科学探疑-网友天空-相对论-光速有限性与分立对称性
![]()
光速有限性与分立对称性
高连全(南京工业职业技术学院)
摘要:本文从光速的有限性出发,推导出两组不同的洛伦兹收缩和变换方程,得出了运动物体所存在的两种相对论效应,并以中性长寿命![]() 介子的衰变
介子的衰变![]() 为例,说明了:这两组方程对分立对称性的适用性;同时指出:正是这两种效应的存在导致了分立对称性的失效。
为例,说明了:这两组方程对分立对称性的适用性;同时指出:正是这两种效应的存在导致了分立对称性的失效。
引子:关于“高速运动物体的成像问题”的再思考
任一观测者观测任一物体,必须通过该物传来的信息才能知。
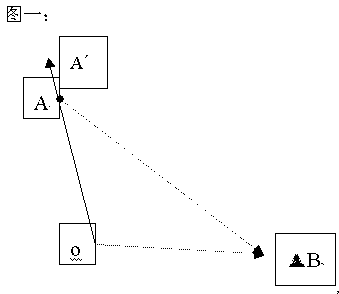
(图一)
如图一、一物体从![]() 出发以速度
出发以速度![]() 运动,同时向观测者B发出第一个光子,经过时间
运动,同时向观测者B发出第一个光子,经过时间![]() 到达
到达![]() 。在
。在![]() 处发出第n个光子,这个光子经过时间
处发出第n个光子,这个光子经过时间![]() 后到达B。在
后到达B。在![]() 时间内物体又向前运动了
时间内物体又向前运动了![]() 距离,到达
距离,到达![]() 。在狭义相对论中,由于没有考虑光速的有限性,因而认为在
。在狭义相对论中,由于没有考虑光速的有限性,因而认为在![]() 时刻物体仍处于
时刻物体仍处于![]() 。后来有学者认识到这一点,但却用“高速运动物体的成像问题”来加以解释。本文作者认为有必要就此进行讨论。
。后来有学者认识到这一点,但却用“高速运动物体的成像问题”来加以解释。本文作者认为有必要就此进行讨论。
一、光速有限性引起的两种相对论效应
从图一可知,![]() 是观测者B在没有收到光子的情况一发生的,因而作者称
是观测者B在没有收到光子的情况一发生的,因而作者称![]() 为不可知量。
为不可知量。
![]() (1-1)
(1-1)
因为: ![]()
所以: ![]() (1-2)
(1-2)
图二是狭义相对论常用的假想试验:
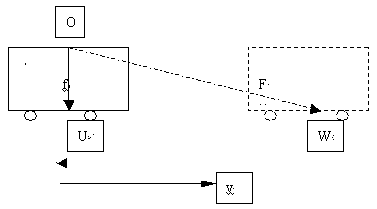
(图二)
一列快车运动速度为![]() ,从车顶上发出一列光,垂直传到地板上。车上观测者乙测得光的路径是垂直线
,从车顶上发出一列光,垂直传到地板上。车上观测者乙测得光的路径是垂直线![]() ,路旁观测者甲测得的路径是斜线
,路旁观测者甲测得的路径是斜线![]() 。由于不可知量的存在,假设乙测到光在
。由于不可知量的存在,假设乙测到光在![]() 时,实际光已到
时,实际光已到![]() ;甲在测量到光在
;甲在测量到光在![]() 时,实际光已到
时,实际光已到![]() 。这样,根据式(1-2)得到:
。这样,根据式(1-2)得到:
![]()
![]()
![]()
(![]() 和
和![]() 分别表示甲、乙所测得的光传播时间、时间不可知量,
分别表示甲、乙所测得的光传播时间、时间不可知量,![]() 表示光速。)
表示光速。)
由勾股定理知:![]()
展开并整理得:
![]() (1-3)
(1-3)
令(1-3)式两边等于0,得到两个二次方程:
方程一:![]()
以T为未知数,解得:
![]()
方程二:![]()
以T′为未知数,解得:
![]()
甲乙两人观察到的光传播时间的关系可用T与T′相比来表示,得:
![]() (1-4)
(1-4)
分别书写并整理得:
![]() (1-5)
(1-5)
或![]() (1-6)
(1-6)
式(1-5)和(1-6)说明:两个参照系在测量的时间的变换上存在两种变换关系。
同样,用推导洛伦兹收缩的一般方法,引入不可知量后可以得到两种空间收缩:
![]() (1-7)
(1-7)
或![]() (1-8)
(1-8)
同样,借助推导洛伦兹变换方程的一般方法可以得到:
![]() (1-9)
(1-9)
![]() (1-10)
(1-10)
![]() (1-11)
(1-11)
![]() (1-12)
(1-12)
根据(1-1)式可将![]() ,还原为:
,还原为:![]() 和
和![]() ,对于
,对于![]() 和
和![]() 它们必定满足测不准原理:假定测量达最大精度,即
它们必定满足测不准原理:假定测量达最大精度,即![]() ,改写成:
,改写成:
![]() (1-13)
(1-13)
从德布罗意波知:![]()
即:
![]() (1-14)
(1-14)
又从多普勒效应知:
![]() (1-15)
(1-15)
即:![]() (1-16)
(1-16)
把(1-15)式代入(1-5)到(1-12)式中,可得到两组变换方程:当选择“+”时,可得第一组:
![]() (1-17)
(1-17)
![]() (1-18)
(1-18)
![]() (1-19)
(1-19)
![]() (1-20)
(1-20)
Y=Y′ (1-21)
Z=Z′ (1-22)
当选择“-”时,可得第二![]() 组:
组:
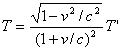 (1-23)
(1-23)
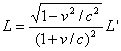 (1-24)
(1-24)
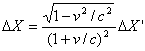 (1-25)
(1-25)
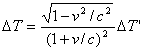 (1-26)
(1-26)
![]() (1-27)
(1-27)
![]() (1-28)
(1-28)
显然,第一组方程(1-17)到(1-22)是洛伦兹变换方程,而另一组方程(1-23)到(1-28)则是另一种变换方程。
综上所述,运动物体在空时变化上存在两种效应,一种是满足洛伦兹变换的相对论效应,另一种则不是。现将这两种变换、两组方程、以及对应的空时效应分别称为正、负变换;正、负效应。
二、两种效应对分立对称性的影响
上节因正负号选择而产生的正、负方程组,是同一个二次方程的两个解,是在完全相同的条件下产生的。在相同的条件下,这两个解都满足方程,任一物理过程中的任一物体,不可能同时存在两个状态。因此,只能认定是同一过程的两个物体或者是相同物体的两个过程,同时,依据其因子![]() 前正负号相反这一唯一区别,对这两组方程的物理意义只能认定:在两个物理过程中的相同物体(或同一物理过程中的两物体),除了其中某一物理量的符号完全相反外,其它的一切条件和性质都是相同的。而符合这些要求的物理现象,只有PCT反演过程,即分立对称性问题。
前正负号相反这一唯一区别,对这两组方程的物理意义只能认定:在两个物理过程中的相同物体(或同一物理过程中的两物体),除了其中某一物理量的符号完全相反外,其它的一切条件和性质都是相同的。而符合这些要求的物理现象,只有PCT反演过程,即分立对称性问题。
现以中性长寿命介子K0L在磁场中的三体半轻子衰变为例讨论。
![]() (1-1)
(1-1)
(2-1)式意味着产生e+这种衰变方式(称之为反衰变)比产生e-的衰变方式(称之为正衰变)要快。
在同一样本中,这两种衰变的一切条件都是相同的,只是粒子的电性相反,这一过程完全符合上节所述的正负方程组的应用条件,其中必然有一种衰变生成粒子的相对论效应是符合正变换,而另一种符合负变换。
比较两种效应的因子:
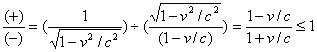 (2-2)
(2-2)
(2-2)式表明,遵循负变换规律的物理过程,其相对论效应更强,即空间收缩与时间膨胀更严重(空间和时间的数值更小了)。
按照衰变的指数定律:
![]() (2-3)
(2-3)
这是个递减的指数函数:T越小、I越大,即时间T数值越小,这种衰变生成的粒子越多。因而可以认定在(2-1)式的两个过程中。反衰变遵循的是负变换效应,正衰变遵循正变换效应。从式(1-15)至(1-20)可以看出正衰变遵循的正变换效应就是相对论效应。
回到(1-7)、(1-8)式,并改写成:
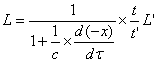 (2-4)
(2-4)
或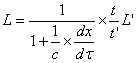 (2-5)
(2-5)
(2-4)和(2-5)式可看成是作P变换,即![]() ,这一变换的值是式(1-16)、(1-22)。很显然,两者是不对称的。
,这一变换的值是式(1-16)、(1-22)。很显然,两者是不对称的。
同样,把(1-5)、(1-6)式改写成:
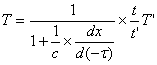 (2-6)
(2-6)
或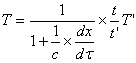 (2-7)
(2-7)
(2-6)、(2-7)式可看成是作T变换,即![]() ,这一变换的结果分别是(1-15)、(1-21),两者也不对称[为避免符号混乱(2-4)到(2-7)式中时间微分用
,这一变换的结果分别是(1-15)、(1-21),两者也不对称[为避免符号混乱(2-4)到(2-7)式中时间微分用![]() 表示]。
表示]。
C变换过程中相共轭的两个粒子,它们的速度必然是等值并反方向的,即![]() ,可以看作P变换。对其电性相反这一唯一差别,根据费曼图,可以将其中任意一个粒子看作其反粒子的逆时运动:
,可以看作P变换。对其电性相反这一唯一差别,根据费曼图,可以将其中任意一个粒子看作其反粒子的逆时运动:![]() ,即T变换。因此,C变换从本质上看是PT联合变换。
,即T变换。因此,C变换从本质上看是PT联合变换。
综上所述,可得表一:
变换 |
P |
T |
C |
操作 |
x→-x |
t→-t |
c→c+ |
因此,对P、C、T的单项变换、两组合变换、三组合变换结果都可以通过下表来反映。
表二:
| 变换 | 操作内容 | 操作结果 | 结论 |
| P | x→-x | x→-x | 不对称 |
| T | t→-t | t→-t | 不对称 |
| C | c→c+(x→-x;t→-t) | x→-x t→-t |
不对称 |
| PT | x→-x; t→-t |
x→-x t→-t |
不对称 |
| PC | x→-x; c→c+(-x→x;t→-t) |
x→x t→-t |
不对称 |
| TC | t→-t; c→c+(x→-x; -t→t) |
x→-x t→t |
不对称 |
| PTC | x→-x; t→-t; c→c+(-x→x; -t→t) |
x→x t→t |
对 称 |
从表二可以看出:在P、C、T这三种分立对称性中,单纯的一种或任意两组合的变换都是不对称的,但PCT三组合的变换却是对称的。
结论:从光速有限性得出运动物体在空时变化上存在着强度不同的两种相对论效应,符合这一特性的物理过程只有分立对称性问题,着强度不同的两种相对论效应,从根本上破坏了分立对称性,但PCT联合对称性却是成立的。
参考书目:
1、曾谨言,《量子力学》,科学出版社,1981年。
2、李政道,《粒子物理与场论简引》,科学出版社,1984年。
3、K.W.Ford,《经典和近代物理学》,陈纲译,高等教育出版社,1983年。
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑