物理科学探疑-网友天空-力学-含库仑定律的新牛顿力学
含库仑定律的新牛顿力学
付昱华
（中国海洋石油研究中心，北京4728信箱，100027, E-mail: fuyh@cnooc.com.cn ）
摘 要:
提出含库仑定律的新牛顿力学。新牛顿力学可以处理水星近日点进动问题和光线近日偏折问题，因而可以部分取代相对论。目前新牛顿力学主要包括六条定律：源定律、改进的万有引力定律、改进的库仑定律和改进的运动三定律。其中将能量守恒定律作为新牛顿力学的源定律，根据源定律可以导出改进的万有引力定律、改进的库仑定律和改进的第二运动定律。原有的第二定律及万有引力定律、库仑定律是根据实验结果总结出来的，为了探讨从理论上导出这三个定律的可能性，根据能量守恒定律，针对一个受约束运动实例（小球沿长斜面滚下），给出导出改进的牛顿第二定律及改进的万有引力定律、改进的库仑定律的方法。适用于本例的常维分形形式的结果：改进的万有引力定律
,,
改进的库仑定律
，改进的牛顿第二定律
。对于静止状态或自由落体运动和带电物体做中心对中心运动，从理论上严格导出（不需要任何实验结果）原有的牛顿第二定律
，并且近似导出原有的万有引力定律、原有的库仑定律。也就是说，对此情况上述三个原有定律成立。在此基础上，对小球沿长斜面滚下导出更精确的变维分形结果：改进的牛顿第二定律
；改进的库仑定律
；其中
为小球滚下的水平距离。对于这个实例，如果要求计算结果具有5位有效数字，则狭义相对论的结果与原有的第二定律结果一样。
新牛顿力学可以解决相对论无法解决的问题。例如物体沿固定曲线运动等受约束时的运动。而对于光线近日偏折的实验结果与广义相对论结果的微小偏差，用新牛顿力学给出的三阶引力公式可以得到与实验结果完全一致的结果。新牛顿力学还可以解决微观物理问题。
关键词:牛顿力学，新牛顿力学，改进的万有引力定律，改进的库仑定律，改进的第二运动定律，理论推导
牛顿是人类历史上最伟大的科学家。牛顿力学曾经有过辉煌的历史。但是，经过几百年之后，牛顿力学的基本形式和主要公式几乎没有任何变化。这种情况似乎也是不正常的。进入新世纪之后，有必要提出与相对论相辅相成的新牛顿力学。
为什么要提出与相对论相辅相成的新牛顿力学？可以从以下几方面论述。
首先，逆向思维是一种成功的思维方式。在讨论牛顿力学与相对论的关系时，一般认为，相对论吸收了牛顿力学的合理部分，并在特殊情况下回复到牛顿力学的某些结论。根据逆向思维的原则，是否可以让牛顿力学吸收相对论的合理部分，并在特殊情况下回复到相对论的某些结论？根据这一思路，我们提出与相对论相辅相成的新牛顿力学。当然，我们还要求新牛顿力学能够解决某些相对论所不能解决的问题。
其次，否定之否定规律是辩证法的基本规律之一。爱因斯坦方法否定了牛顿方法，如果否定之否定规律继续适用，则应该再由牛顿方法否定爱因斯坦方法。再由牛顿方法否定爱因斯坦方法的原因如下。
到目前为止，主要存在两种建立物理学理论的方法：牛顿方法和爱因斯坦方法。牛顿方法可以称为绝对自由或不受限制的方法。爱因斯坦方法可以称为相对自由或受对称性限制的方法。
在牛顿生活的年代及其以前的很长一段时间里，在人们的心目中，亚里士多德、欧几里德、阿基米得等古希腊的先贤是不可逾越的高峰。任何人，在不引经据典的情况下都不敢提出新理论。而牛顿，以大无畏的精神突破了这一限制，建立了全新的，而且远远超过希腊人的理论体系。所以我们说，牛顿方法可以称为绝对自由或不受限制的方法。具体地说，即以实验和事实为依据，在一切可能的方案之中，选择最佳方案。
而爱因斯坦在建立理论体系之前，先追求数学上的完美性。对于数学上不完美的理论，则将其拒之门外。按现在的说法，爱因斯坦建立的理论属于对称性理论。所以我们说，爱因斯坦方法可以称为相对自由或受对称性限制的方法。具体地说，即以实验和事实为依据，仅在对称性方案之中，选择最佳方案。
牛顿方法的优点是不会遗漏可能获得成功的方案，缺点是可供选择的方案太多。爱因斯坦方法的优缺点与牛顿方法正好相反。其优点是可供选择的方案较少，缺点是可能会遗漏能够获得成功的方案。
最成功的对称性理论，广义相对论（是否定牛顿理论的产物）的灿烂光辉已经逐渐消退。许多人正与相对论作对。而且，一些原来必须用相对论求解的问题，如水星近日点进动问题，特别是光线近日偏折问题，现在用牛顿力学方法也能求解[1]。
牛顿之前是“言必称希腊”。爱因斯坦之后是“言必称对称”，时至今日，这种状态应该而且也必须打破。
相信将有越来越多的人宁可用牛顿方法，而不愿冒险用爱因斯坦方法，因为牛顿方法保险，而一旦选择了错误的方法，将会浪费无穷多的时间和精力。
需要指出的是：数学上完美的理论只能近似地反映自然规律。以对称为例，宇宙间有完全对称的事物吗？没有。至少现在还没有发现。例如雪花，边角处总有破缺，因此只是近似对称。同样，目前所有的对称理论都遭遇对称性破缺。既然如此，就应该说：爱因斯坦方法只能对事物进行近似描述，而要更精确地对事物进行描述，必须回归到牛顿的出发点，开辟新牛顿之路，建立新牛顿力学。
原有的牛顿力学主要包括四条定律：万有引力定律和运动三定律。几百年来，在工程等领域的实际应用中，这四条定律的形式没有任何改进。但是，原有的牛顿力学的美中不足之处，是不容置疑的。
原有的万有引力定律不能处理水星近日点进动问题和光线近日偏折问题，需要用广义相对论来处理。但是，导出广义相对论的场方程时，只考虑物体依据惯性在引力场中的运动。因此严格地讲，原有的万有引力定律和广义相对论实际上只能处理物体依据惯性在引力场中的运动，而不能处理物体还受到其他约束时的运动。针对这些情况，有必要在经典力学的框架内提出新牛顿力学，使之能够处理水星近日点进动问题和光线近日偏折等问题，以及物体在引力场中受到其他约束时的运动。
新牛顿力学主要包括六条定律：源定律、改进的万有引力定律、改进的库仑定律和改进的运动三定律。其中将能量守恒定律作为新牛顿力学的源定律，根据源定律可以导出改进的万有引力定律、改进的库仑定律和改进的第二运动定律。原有的第二定律及万有引力定律、库仑定律是根据实验结果总结出来的，为了探讨从理论上导出这三个定律的可能性，根据能量守恒定律，针对一个受约束运动实例（小球沿长斜面滚下），给出同时导出改进的牛顿第二定律、改进的万有引力定律及同时导出改进的牛顿第二定律、改进的库仑定律的方法。具体给出适用于本例的常维分形形式的结果以及变维分形形式的结果。
一、原有牛顿力学的四条定律和库仑定律
原有的牛顿力学主要包括四条定律：万有引力定律和运动三定律。
牛顿提出的万有引力定律的形式为
(1)
库仑定律是根据实验结果总结出来的。库仑提出的库仑定律的形式为
(1')
牛顿提出的运动三定律为
第一定律：任何物体都保持静止的或匀速直线运动的状态，直到其他物体的作用迫使它改变这种状态为止。
牛顿提出的第二定律的形式为
(2)
第三定律：两物体间的一对相互作用，永远等值反向，且在同一直线上。
二、新牛顿力学六定律
新牛顿力学主要包括六条定律：源定律、改进的万有引力定律、改进的库仑定律和改进的运动三定律。
能量守恒定律是自然界的一条基本定律。主要内容为：在封闭系统中，系统的总能量保持不变。
新牛顿力学将能量守恒定律作为源定律，根据源定律可以导出其他定律。
新牛顿力学中，既要照顾传统，又要考虑创新，因而将改进的万有引力定律采用两种形式：级数形式和分形形式。
级数形式包括一阶近似公式，二阶近似公式和高阶近似公式。
一阶近似公式即为原有的万有引力定律（1）式。二阶近似公式为笔者在参考文献[1]中借助于广义相对论导出的行星运动方程所给出的改进的万有引力公式
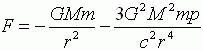(3)
式中：G为引力常数；M和m为两物体的质量；r为两物体间的距离；c为光速；p为质量为m的物体在质量为M的物体的引力场中沿圆锥曲线运动时的半正焦弦，而且有：p
= 
,对于椭圆；
，对于双曲线；
，对于抛物线。
当两物体做中心对中心运动（含相对静止）时，可视为半正焦弦p = 0的情况，此时改进的万有引力公式与原有的万有引力公式相同。该公式对水星近日点进动问题和光线近日偏折问题均能给出与广义相对论一样的正确解。
但是，公式（1）和（3）只能处理两物体做中心对中心运动（含相对静止）和质量为m的物体在质量为M的物体的引力场中沿圆锥曲线运动时的情况，对于受约束等情况而作非中心对中心直线运动（不含相对静止）和沿其他曲线运动的情况，就要讨论更一般形式的高阶近似公式。
参照（3）式，可以将高阶万有引力近似公式写为
(4)
类似地，可以将更一般形式的库仑定律写为
(4')
在最近十几年间，分形方法已在一些领域获得成功应用，它被用来揭示复杂现象中深藏的有组织结构。反映有组织结构特征的量称为分维数，用Ｄ值来表示。在目前一般应用的分形方法中，分维数Ｄ为实数，例如不同地段海岸线的分维数Ｄ值可以取为1.02、1.25等。
分形分布可用如下幂指数分布定义[2]
式中：ｒ为特征线度，如长度、时间等；N 为与 ｒ 有关的数量，如力、温度和高度等；Ｃ为待定常数，Ｄ为分维数。
当Ｄ为常数时，这种分形可称为常维分形。
分形形式的万有引力定律写为如下变维分形[3~5]的形式
(5)
也可以将更一般形式的库仑定律写为变维分形的形式：
(5')
式中:
，例如可以令
(6)
关于常维分形和变维分形形式的万有引力定律的量纲问题将在后面讨论。
改进的运动三定律如下。
改进的第一定律：任何物体在与外界没有能量交换的情况下，能量保持不变。特别地，任何物体都保持其固有的运动状态，直到其他物体的作用或其本身的潜能迫使它改变这种状态为止。
改进的第一定律与原有的第一定律的区别在于加进了能量守恒的内容，使其适用范围更广泛。另外，物体本身的潜能也可能改变其运动状态，例如高速转动的物体可能分裂。
改进的第二定律采用两种形式：级数形式和分形形式。
级数形式包括一阶近似公式和高阶近似公式。
一阶近似公式即为原有的第二定律（2）式。
高阶近似公式写为
(7)
分形形式的改进的第二定律写为变维分形的形式
(8)
式中:
， 例如可以令
(9)
为方便计，我们写为
(10)
如果
，则成为原有的牛顿第二定律。
关于常维分形和变维分形形式的改进的第二定律的量纲问题也将在后面讨论。
改进的第三定律：两物体间具有能量交换的情况下，一物体减少的能量，等于另一物体增加的能量。特别地，两物体间的一对相互作用，永远等值反向，且在同一直线上。
改进的第三定律与原有的第三定律的区别在于加进了能量守恒的内容，使其适用范围更广泛。
三、同时导出改进的牛顿第二定律及万有引力定律的变分原理及同时导出改进的牛顿第二定律及库仑定律的变分原理
原有的第二定律及万有引力定律和库仑定律是根据实验结果总结出来的，为了探讨从理论上导出这三个定律的可能性，本文根据能量守恒定律，简述用变维分形方法针对一个实例（小球沿长斜面滚下）同时导出改进的牛顿第二定律及万有引力定律及同时导出改进的牛顿第二定律及库仑定律的的方法。详情请见参考文献[8]和[9](请注意其中坐标选取的方式与本文不同)。
下面用最小二乘法（加权残值法的一种）给出能量守恒定律建立的变分原理。
设封闭系统的初始总能量为
，任意时刻
的总能量为
，则根据能量守恒定律应有
(11)
上式可以写为
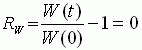(12)
应用最小二乘法，对于区间
，根据能量守恒定律可得如下变分原理
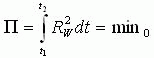(13)
式中：
表示最小值而且应当等于零。是在参考文献[6]中引入的。
需要说明的是，在许多情况下为近似解，因此
并非恒等于零，因此变分原理（13）可以用于求解。这是加权残值法的常用做法，详情请见参考文献[7]。
除了时间坐标以外，还可以采用其他坐标，例如对于区间
，根据能量守恒定律可得如下变分原理
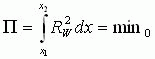(14)
以上是直接应用能量守恒定律建立的变分原理。有时为了导出其他定律等目的，还需要间接应用能量守恒定律建立变分原理。例如我们感兴趣的某一物理量
，将能量守恒定律计算的结果记为
，令
重新定义如下
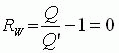(15)
将（15）式代入（13）和（14）式，由于是根据能量守恒定律计算的结果，所以得到间接应用能量守恒定律建立的变分原理。另外，与的符合程度也一目了然。
四、变维分形等形式的改进的牛顿第二定律及万有引力定律
将（4）、（4’）或（5）、(5’)式，（7）或（8）式计算的有关物理量代入（13）或（14）式，根据极值条件可以建立如下方程组
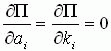(16)
解出此方程组以后，就可以同时得到改进的牛顿第二定律及万有引力定律或同时得到改进的牛顿第二定律及库仑定律。判别解的近似程度可以根据
值接近于零的程而定。值越接近于零，效果越好。
显然，在求解过程中我们没有依赖任何实验结果。不过，这样得到的改进的牛顿第二定律及万有引力定律或库仑定律，是否适用于其他场合，是一个需要进一步研究的课题。之所以要这样说，因为对于不同的场合，引力的规律不一样[10]。
还需要说明的是，除了求解方程组可以确定最小值及各待定常数以外，用最优化算法也可以确定最小值及各待定常数。本文中将用最优化算法确定最小值及各待定常数。
五、同时导出改进的牛顿第二定律及万有引力定律和同时导出改进的牛顿第二定律及库仑定律的实例
下面对于一个实例，同时导出常维分形形式（即（5）式中的 和（10）式中的 均为待定常数）的改进的牛顿第二定律及万有引力定律。本例取自参考文献[8]。
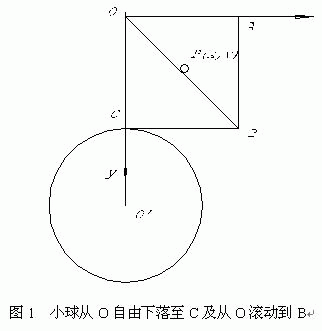
如图1所示，设有一条从O到B的直线（实际上是一个斜面），考虑小球沿直线从O滚动到B的情况。设当小球位于O点时，其初速度为零。假设小球可以视为质点，因而转动能可以忽略不计，摩擦作用也忽略不计。
设圆O’代表地球。地球的质量为M，小球的质量为m。设OO’为一条铅垂线，x坐标与OO’垂直，y坐标与x坐标垂直（与OO’重合）。BC与OO’垂直。OA，AB，BC，OC的长度均为H， O’C的长度等于地球半径R。假设从O到B的直线以及x-y坐标均以某种方式固定于地面，因此可以不考虑地球的运动而只考虑小球在x-y坐标中的运动。
对于本例，我们感兴趣的物理量是小球在点P时速度的平方
,为了便于区别，将改进的牛顿第二定律及万有引力定律计算的结果仍然记为,将能量守恒定律计算的结果记为
，将变分原理（14）重新写为如下形式
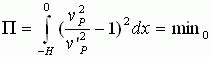(17)
现在我们先根据能量守恒定律计算有关的物理量。
由改进的万有引力定律(5)式可以得到小球位于任意点P时的势能为
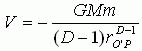(18)
根据能量守恒定律应有
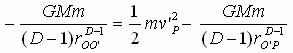(19)
于是有
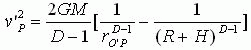(20)
现在我们根据改进的牛顿第二定律及万有引力定律计算有关的物理量。
设小球滚动的直线为
Y = x （21）
当小球运动到任意点P时，由于
dv/dt = a （22）
而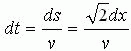
于是有
（23）
根据改进的万有引力定律可得沿切线方向所受力为
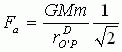（24）
根据改进的牛顿第二定律可得P处沿切线方向的加速度a为
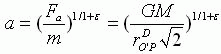（25）
于是由（23）式可得
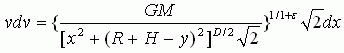（26）
将(21)式代入上式，对两端从O到P进行积分，可得
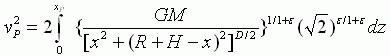（27）
上式可以根据数值积分的方法进行计算。下面进行具体的推导和计算。
已知地球的GM=3.99×1014m3/s2,
地球半径R=6.37×106m, H=R/10, 试对图1问题求解终点B处的
，并同时导出改进的牛顿第二定律及万有引力定律。
首先将能量守恒定律和原有的牛顿第二定律及万有引力定律（即在（5）式中D=2，在（10）式中ε=0）计算的各量代入（17）式，得到
=571.4215。
此时根据能量守恒定律计算的=1.0767×107，根据原有的牛顿第二定律及万有引力定律计算的 =1.1351×107。两者相差5.4%。由于不等于零，就可以用最优化方法确定D和ε。目前应用的最优化方法可以分为两类：一类可以不依赖初值，但程序复杂；另一类要求初值足够好，但程序简单。我们采用后一类中的搜索法[6]。
先固定D值，令D=2，然后搜索ε值，当ε=0.0146时
达到最小值139.3429；然后固定ε，搜索D值，当D=1.99989时达到最小值137.3238；然后固定D值，搜索ε值，当ε=0.01458时达到最小值137.3231；由于两次搜索后的值极为接近，于是可以停止搜索，得到最后结果
此时值仅为值的24%。而根据能量守恒定律计算的
，根据改进的牛顿第二定律及万有引力定律计算的两者相差仅2.7%。
由此得到适用于本例的改进的牛顿第二定律及万有引力定律如下
改进的万有引力定律
, 改进的牛顿第二定律
现在讨论常维分形形式的牛顿第二定律和万有引力定律的量纲问题。给出两种方案。
第一种方案，规定
的量纲一样。
第二种方案，在每一个公式的右边乘以一个专门处理量纲的常数，例如改进的牛顿第二定律为
的量纲一样。
本文采用第一种方案，其优点是可以不改变公式的形式。而第二种方案需要改变公式的形式。当然，是否还有更好的方案，还可以进一步讨论。
变维分形形式的量纲可以仿此处理。
下面讨论对于这个实例狭义相对论的结果。根据狭义相对论，牛顿第二定律的形式为
(28)
式中：
对于图1所示情况，由（28）式可得
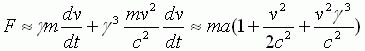(29)
代入(29)式可得
因此，对于本文实例，如果要求计算结果具有5位有效数字，则狭义相对论的结果与原有的第二定律结果一样，即与能量守恒原理的结果不符。
下面讨论同时导出改进的牛顿第二定律和库仑定律。
在图1中，设圆
代表带电大球体。带电大球体的电量为
,带电小球的质量为
,
点时，其初速度为零，引力和摩擦作用也忽略不计。已知图1问题带电球体及带电小球的
,带电球体半径
,并同时导出改进的库仑定律及牛顿第二定律。
具体推导过程类似于同时导出改进的牛顿第二定律和万有引力定律，详细过程见参考文献[9]，由此得到适用本例的改进的库仑定律及牛顿第二定律如下：
改进的库仑定律 
改进的牛顿第二定律
上面是常维分形的结果，下面讨论变维分形的结果。
首先对某种情况严格导出原有的牛顿第二定律及近似导出原有的万有引力定律。
现在必须假设原有的万有引力定律及原有的牛顿第二定律的形式为：
式中: D和D’为待定常数，需要我们来导出。
假设有一个物体从距离地面高度为H的地方（O点）自由下落至地面（C点）。
对于本例，我们感兴趣的物理量是小球在点P时速度的
,为了便于区别，将改进的牛顿第二定律及万有引力定律计算的结果仍然记为,将能量守恒定律计算的结果记为
.
现在我们先根据能量守恒定律计算有关的物理量。
根据能量守恒定律应有
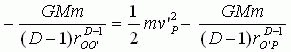
于是有
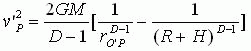
现在我们根据改进的牛顿第二定律及万有引力定律计算有关的物理量。
根据牛顿第二定律可得P处的加速度a为
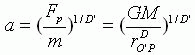
，于是有
由此可得
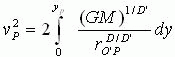
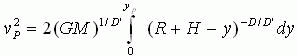
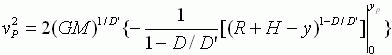
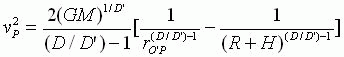
如果要求
,则应有
上面的两个公式均可以得到
于是对自由落体问题严格导出了原有牛顿第二定律
于是对自由落体问题严格导出了原有牛顿第二定律 。
但是此时不能导出原有的万有引力定律，因D值可以是任意常数。
下面近似导出原有的万有引力定律。
从上面对小球沿长斜面滚下的讨论可知，当H=R/10时，可得
同样，当当H=R/20时，可得
至此近似导出了原有的万有引力定律。至于如何严格导出原有的万有引力定律，将是进一步研究的课题。
类似地，可以近似导出原有的库仑定律。
考虑到静止状态或自由落体运动和带电物体做中心对中心运动时原有的万有引力定律、原有的库仑定律及原有的牛顿第二定律精确成立，因此三个改进的定律在初始位置都应该还原为原有的万有引力定律、原有的库仑定律及原有的牛顿第二定律。但是常维分形的结果无法满足这一条件。因此需要导出更精确的变维分形结果。
设改进的牛顿第二定律为
;改进的万有引力定律为
;改进的库仑定律为
;其中
为小球滚下的水平距离。
用与常维分形类似的方法（详细过程将在另文中发表），得到变维分形的结果
变维分形的结果要大大优于常维分形的结果。例如在同时导出改进的牛顿第二定律及万有引力定律时得到的最后结果为
值的0.033
%。而根据能量守恒定律计算的
,根据改进的牛顿第二定律及万有引力定律计算的
.
六、用新牛顿力学解决相对论无法解决的问题
对于光线近日偏折问题，应用改进的牛顿万有引力公式，在牛顿力学范围内也可以得出与广义相对论相同的偏折角度。应用广义相对论或改进的牛顿万有引力公式得出的这一偏折角度
为，
（30）
但是，许多次观测结果却与这一角度有微小的差别。现在，人们正在考虑消除其他因素（如日冕等）的影响，得出纯粹由引力作用引起的偏折角度是否与（30）式相同，以便确定广义相对论的误差。
必须考虑的问题是，如果精确的测量表明，纯粹由引力作用引起的偏折角度与广义相对论得出的这一偏折不一样，将如何处理？这个问题迟早肯定会发生的，因为广义相对论再精确，也不可能在小数点以后任意位置上都是准确的。面对这个问题，如果要再改进广义相对论，创立新的理论，其困难程度可想而知。但是，如果用新牛顿力学方法，则很容易寻求更精确的光子所受引力的公式（至于此公式是否适用于其他场合，则是进一步研究的课题）。
现在应用如下形式的高阶引力公式
式中：
。
由于实验值与广义相对论或改进的牛顿万有引力公式得出的偏折角度的差别极小，换句话说，改进的牛顿万有引力公式已经相当精确，因此可以将其再加一修正项作为光子所受三阶引力的公式：
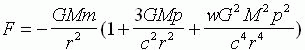（31）
式中：w为待定常数。
下面将根据实验结果确定w值。具体过程见参考文献[10]，此处略去。
经过计算可得偏折角度为
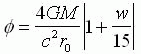（32）
式中： r0为太阳半径。
因为
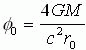（33）
由于w为一小量，因而可得
（34）
由此可解出w值
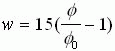（35）
现在就可以根据实验结果确定w值。表1给出了光线近日偏折角度的射电天文学实验数据。
表1 光线近日偏折角度的射电天文学实验数据
| 年代 观测者 观测值/ ” |
| 1969
G.A.Seielstud等
1.77±0.20 1969 D.O.Muhleman等 1.82+0.24-0.17 1969 I.I.Shapiro 1.80±0.2 1970 R.A.Sramak 1.57±0.08 1970 J.M.Hill 1.87±0.3 1972 1.82±0.14 1974 1.73±0.05 1975 1.78±0.02 |
我们选择1975年的实验数据，即有
（36）
于是可得
0.08571≤w ≤0.42857 （37）
如果取平均值，可得
w=0.25714 （38）
由此，根据实验结果反推出了光子所受的引力。
如果以后有更准确的实验数据，则可以得到更准确的w值。
七、结论
本文在经典力学的框架内提出与相对论相辅相成的新牛顿力学。新牛顿力学主要包括六条定律：源定律、改进的万有引力定律、改进的库仑定律和改进的运动三定律。牛顿第二定律及万有引力定律、库仑定律是根据实验结果总结出来的。文中实例表明原有的牛顿第二定律及万有引力定律、库仑定律需要改进。为了从理论上导出这三个定律，可以根据能量守恒定律，用变维分形方法针对一个实例（小球沿长斜面滚下）同时导出改进的牛顿第二定律及改进的万有引力定律、同时导出改进的牛顿第二定律及改进的库仑定律。用新牛顿力学可以部分取代相对论及解决相对论无法解决的问题。由于能量守恒定律同样适用于微观物理现象，因此新牛顿力学也可以处理微观物理问题。
参 考 文 献
1 付昱华. 改进的牛顿万有引力公式. 自然杂志. 2001年1期:58~59
2 Turcotte D L. Fractals and chaos in geology and geophysics. Cambridge:
Cambridge University Press,1992. 1~22
3 付昱华.
流体力学中的变维分形，第二届全国计算水力学会议论文集，1993年，武汉
4 付昱华. 分形技术在油气勘探应用中的改进 —
变维分形技术，中国海上油气(地质)，1994年3期
5 Fu Yuhua, Analysed and fractal single point method for solving hydraulic problems in
ocean
engineering, International meeting on petroleum engineering, SPE 29986, Nov., 1995,
Beijing
6 付昱华. 水星进动问题新解，天文学报，1989年4期:350~354
7 徐次达，陈学潮，郑瑞芬.
新计算力学加权残值法，同济大学出版社. 1997，1~6，353~355
8
付昱华，分形方法导出改进的牛顿第二定律及万有引力定律，中国工程科学,
2003，5（6）
9
付昱华，库仑定律和牛顿第二定律的理论推导，广西科学, 2003年2期
10 付昱华. 非平方反比引力定律，沙洋师专学报，2002年6期
New Newton’s Mechanics Including Law of Coulomb
Fu Yuhua
（China Offshore Oil Research Center, P.O.Box 4728,Beijing, 100027，E-mail: fuyh@cnooc.com.cn ）
Abstract This paper presents the New Newton’s mechanics
complemented by relativity within the frame of classical mechanics. New Newton’s
mechanics can be used for solving the problem of advance of Mercury’s perihelion and the
problem of light deflection around the Sun. Therefore it can be used for partly replacing
relativity. New Newton’s mechanics mainly includes six laws: source law, improved law of
gravity, improved law of Coulomb and three improved movement laws. The law of conservation
of energy is the source law of New Newton’s mechanics. The existing Newton’s second
law, the law of gravity and the law of Coulomb are summarized with experimental results.
For discussing the possibility of deriving these three laws theoretically, according to
the law of conservation of energy, the method of deriving improved Newton’s second law
and the law of gravity at one time, and the method of deriving improved Newton’s second
law and the law of Coulomb at one time with variable dimension fractal method is presented
for an example (a small ball moves down along a long incline). The results suitable for
this example with the constant dimension fractal form are as follows: improved law of
gravity
，improved
law of Coulomb 
，improved Newton’s second law
.Considering
that for the cases of static state or free movement and center to center movement the
original Newton’s second law, the original law of gravity and the law of Coulomb are
correct exactly, the more accurate results with the form of variable dimension fractal are
as follows: improved Newton’s second law 
;improved law of Coulomb
;where
equals the horizontal distance of the small ball movement. To the example given in this
paper, for the result of five significant digits, the special relativity will give the
same result as give by the original Newton’s second law. New Newton’s mechanics can be
used for solving the problem which can not be solved by relativity. For example, a body
moves along to a fixed curve, and other restricted movements. As for problem of light
deflection around the Sun, to the little warp between experiment result and the one given
by general relativity, the three order gravitational formula derived by new Newton’s
mechanics can be used for giving the same result as given by experiment.
Key words: Newton’s mechanics, New Newton’s mechanics, Improved law of gravity, Improved law of Coulomb Improved Newton’s second law, Theoretical derivation
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑