物理科学探疑-网友天空-空间与介质-“R物质”的发现
![]()
“R物质”的发现
芦光耀
我已证明:电场、磁场、重力场是由同一种物质作不同类型的运动而形成的;换句话说,它们是同一种物质的三种形态。我命名这种物质为“R物质”。关于“R物质”的存在,我可以提供实验的证明。根据该观点而建立的理论不仅完美地解释了“电磁学”,而且解答了一些基础问题,如:电荷、地球等是如何形成的?为什么同种电荷(或磁极)相斥而异种电荷(或磁极)相吸呢?等等……
“R物质”存在的证明
前言:我将分三个步骤来证明“R物质”的存在,即用“R物质”分别描述电场、磁场和重力场,并以“R物质”的运动规律对它们的基本性质加以证明。为了使证明的主线清晰,我增加了一个说明部分,把一些关连性的说明或证明放到了说明部分。
第一部分:电场
电场是由大量的“R物质”微粒按直线或曲线规律运动而形成的。实际电场还含有波动的成分。也就是说电场是从实际电场中分离出来的一个分量。需要说明的是,就电场而言,单粒“R物质”的行为是毫无意义的,而大量“R物质”的运动行为才有可能表现为电场。换句话说,电场是大量“R物质”运动微粒的一种集体表现。
静电场起源于电荷。
1.对“R物质”的不断发射或吸收形成了电荷的场。
正电荷不断地发射“R物质”,而负电荷不断地吸收“R物质”。当正负电荷相互靠近时就会相互吸引,即产生了静电力。在此必须说明两点,1).负电荷随然在不断地吸收“R物质”,但负电荷本身在外界的作用下存在着一种循环机制,使其内部的“R物质”不会无休止地增加(详情见说明1)。2).由于正电荷不断地发射“R物质”,因此正电荷是在不断地衰减的,但因“R物质”微粒太小而组成电荷的“R物质”微粒数目又太大了,因此它的衰减速度,以我们人类对时间的感觉来讲,是非常缓慢的。然而自然界中,有许多物质不是存留了数千甚至数万年吗?这仅是一种表面现象。实际上,其内部存在着一种替换机制,这和溶解结晶有关(详情见说明2)。
2.实际电场可分解为波动成分和电场成分。
在正电荷向四周发射“R物质”的过程中,“R物质”的运动具有如下特点:1).“R物质”的运动是靠微粒间的多级碰撞而进行的。2).“R物质”的运动既含有波动的成分又含有直线运动的成分。其中波动成分既含有沿径向的径向振动又含有沿垂直于径向的横向振动。波动成分的主要作用是,1).传播“R物质”运动的振动能量。2).均化“R物质”微粒的位置分布和能量分布。直线运动成分的主要作用是,1).传播“R物质”微粒的直线运动能量。2).传播扩散“R物质”微粒的直线位移。要研究实际电场中某一区域“R物质”微粒的平均速度或平均密度的话,在波动成分的能量远大于直线运动成分的能量条件下,可以忽略波动成分而研究其中的直线运动成分(即:电场成分),如图1-1、图1-2和图1-3。
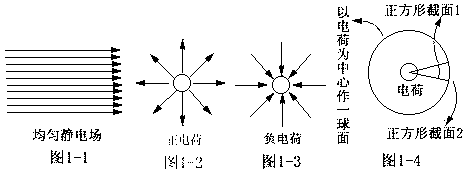
在图1-1、图1-2和图1-3中,微粒沿图示箭头方向作匀速直线运动,且“R物质”微粒之间并不发生碰撞作用。在图1-1中,“R物质”微粒的位置和能量是沿图示空间均匀分布的。在图1-2和图1-3中,“R物质”微粒的位置和能量是沿径向空间均匀分布的。沿径向空间均匀分布是指:如图1-4所示。在图1-4中,两截面中的“R物质”微粒数目相同,且截面1中“R物质”微粒的平均速率等于截面2中“R物质”微粒的平均速率,而且“R物质”微粒在两截面中都是均匀分布的。
3.电荷的受力规律和密度分布规律。
电荷受力规律:若电荷两侧区域的“R物质”平均密度不相同,则电荷将受到力的作用,力的方向是指向平均密度小的一方(电荷受力规律的证明见说明3)。
密度分布规律:在“R物质”运动过程中,若某区域“R物质”微粒的平均速率增大了,则该区域“R物质”的平均密度将减小。反之,若某区域“R物质”微粒的平均速率减小了,则该区域“R物质”的平均密度将增大(密度分布规律的证明见说明4)。
4.电荷之间产生力的原因。
| 先从正负电荷谈起,如图1-5所示。实际上,如果正负电荷量相等的话,正电荷发出的微粒数目应等于负电荷吸收的微粒数目,因此在正负电荷同时存在的情况下,就电场中的某一微粒而言,它既是正电荷发出的同时也是负电荷要吸收的,因此可把该微粒在正电荷单独存在时该微粒运动的速度矢量和负电荷单独存在时该微粒运动的速度矢量进行叠加。在图1-5中,为了简化分析,设正负电荷量相等。根据叠加原理可知,在正负电荷之间的内侧区域中,“R物质”微粒运动的平均速率增大了,平均速率增大是相对于正电荷或负电荷单独存在时的情况。根据密度分布规律可知,在该区域中,由于微粒运动的平均速率增大了,因此,微粒的平均密度将减小。同理,在正负电荷的外侧区域中,根据叠加原理可知,“R物质”微粒运动的平均速率减小了。根据密度分布规律,在该区域中,由于微粒运动的平均速率减小了,因此,微粒的平均密度将增大。 | 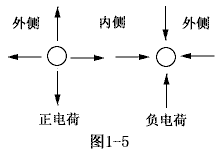 |
由以上分析可知,在上图中,内侧微粒的平均密度小于外侧微粒的平均密度。根据电荷受力规律,正负电荷均应受到指向内侧的力,因此,正负电荷就表现为相互吸引,即产生了引力。
同性电荷相斥的证明方法和上述方法大同小异。这里仅就证明结果介绍如下:同性电荷之间产生斥力的原因是由于它们内侧的“R物质”平均密度大于其外侧的“R物质”平均密度,因此,它们均应受到指向外侧的力,于是同性电荷就表现为相互排斥,即产生了斥力。
因此,电荷之间的力是它们的电场相互作用而产生的。
5.电场力
|
我们知道,电场力是就电荷而言的。在电场中,电荷受力情况的证明方法和上述方法大同小异。这里仅就证明结果介绍如下:如图1-6和图1-7所示。 1).负电荷:如图1-6所示。负电荷在电场中的受力原因是由于其右侧区域“R物质”的平均密度大于其左侧区域“R物质”的平均密度,于是受到指向左侧的力,因此负电荷应逆电场方向而行。 |
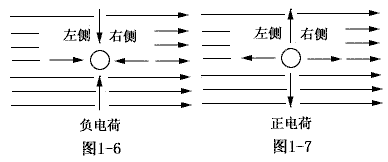 |
2).正电荷:如图1-7所示。正电荷在电场中的受力原因是由于其左侧区域“R物质”的平均密度大于其右侧区域“R物质”的平均密度,于是将受到指向右侧的力 ,因此正电荷应顺电场方向而行。
电场部分的证明到此为止。由于电场的其它性质涉及到了磁场,因此我会在以后的证明中加以表述的。
第二部分:磁场
磁场是由“R物质”同时作大量的螺旋运动而形成的。如图2-1所示。
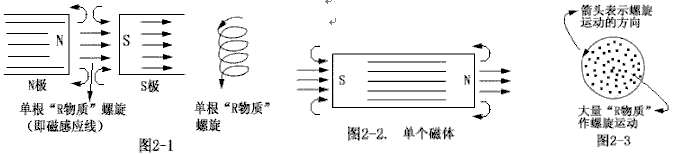
单根“R物质”螺旋就是一根磁感应线,而磁场中某点磁感应强度的大小和该点微小区域范围内所有“R物质”螺旋旋转速率平均值的大小成正比。单根“R物质”螺旋的直径远小于电子的直径,且单根“R物质”螺旋遵从右手法则,即右手四指指向“R物质”微粒作螺旋运动的方向,而母指指向螺旋的旋出方向。磁场是大量“R物质”螺旋的集体表现,因此就磁场而言,单根“R物质”螺旋是毫无意义的。就单个磁体而言,如图2-2所示,沿垂直于单根螺旋轴线方向取一截面,如图2-3所示。图中“R物质”微粒之间并不发生碰撞作用,设该圆形截面内“R物质”微粒运动的平均速率为U,则沿垂直于轴线方向的任意截面内微粒运动的平均速率都近似为U。实际磁场中,“R物质”的运动是通过微粒间的多级碰撞而进行的。可把实际磁场分解为波动成分和磁场成分。如果波动成分的能量远大于磁场成分的能量的话,可近似认为微粒之间的碰撞作用主要发生在波动成分中,而磁场成分中不含有微粒之间的碰撞作用。如果研究磁场中某区域微粒的平均运动速率或平均密度的话,可忽略波动成分。
磁场源于电荷的运动(磁场的形成过程见说明5)。
1. 磁体的受力规律 :
当磁体两侧“R物质”的平均密度不同时,磁体将受到力的作用,力的方向是指向平均密度小的一侧(磁体受力规律的证明见说明6)。
2. 磁极之间产生力的原因。
| 先从异性磁极谈起,如图2-4所示。为了分析方便,设两磁体的大小和磁性完全相同。在磁体1和磁体2单独存在时,从N极出来的磁力线根数应等于从S极进入的磁力线根数。当两磁体相互靠近时,“磁体1”N极的部分磁力线与“磁体2”S极的部分磁力线产生合并,且两磁体越靠近,则参预合并的磁力线数目越多。合并后,两磁体原来的磁力线根数并未发生改变。这样,合并的磁力线既属于磁体1又属于磁体2,因此可利用叠加原理。根据叠加原理,两磁体内侧区域合并磁力线“R物质”螺旋的旋转速率增大,因此内侧区域“R物质”运动的平均速率增大。平均速率增大是相对于两磁体单独存在时的情况。两磁体的外侧区域中,磁力线根数和磁力线“R物质”螺旋的旋转速率都未发生改变,因此,外侧区域“R物质”运动的平均速率并未发生改变。 | 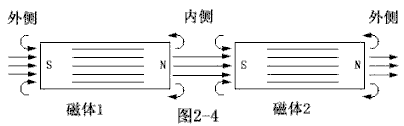 |
由以上分析可知,两磁体内侧区域“R物质”运动的平均速率大于其外侧区域“R物质”运动的平均速率。根据密度分布规律,内侧区域“R物质”的平均密度要小于外侧区域“R物质”的平均密度,根据磁体受力规律,两磁体都将受到指向内侧的力,因此两磁体就表现为相互吸引,即产生了引力。
同性磁极相斥的证明方法和上述方法大同小异。现就证明结果介绍如下:同性磁极相斥的原因是由于两磁体内侧区域“R物质”的平均密度大于其外侧区域“R物质”的平均密度,于是,两磁体都将受到指向外侧的力,两磁体就表现为相互排斥,即产生了斥力。
3. 在磁场中运动电荷的受力原因。
运动电荷本身就产生磁场,因此,电荷在磁场中运动时,它本身所产生的磁场要和原磁场发生作用而使它周围的磁场产生变化,从而使它受到力的作用。请注意,运动电荷是在它周围的磁场发生变化的过程中而受到力的作用的。而磁场在变化过程中要产生感生电场的。
| 下面采取一种简化方法来分析电荷的受力情况。设在均匀磁场中,一正电荷以速度V0沿垂直于磁力线的方向运动,如图2-5所示。运动的正电荷本身所产生的磁场和原磁场的叠加使电荷右侧的磁感应强度增大,使电荷左侧的磁感应强度减小,因此电荷右侧的“R物质”螺旋旋速增大而电荷左侧的“R物质”螺旋旋速减小,因此,电荷右侧区域“R物质”运动的平均速率增大而电荷左侧区域“R物质”运动的平均速率减小。根据密度分布规律,电荷右侧区域“R物质”的平均密度将减小而电荷左侧区域“R物质”的平均密度将增大。注意,右侧区域“R物质”平均密度减小的过程中必伴随“R物质”向该区域周围的扩散,而左侧区域“R物质”平均密度增大的过程中必伴随“R物 | 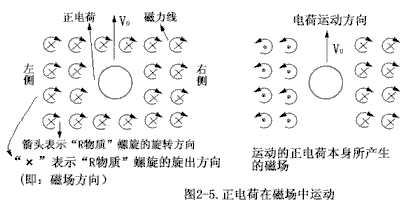 |
质”向该区域内部的收缩,因此这两种过程使在电荷附近形成了一种电场,该电场的方向指向电荷的左侧(即:密度增大的一方)。因此,在磁场中运动的电荷是受到电场力的作用而发生偏转的。需要注意的是,电荷的运动是一种过程,电荷在磁场中的运动过程中而伴随产生了电场,该电场是依赖于电荷运动的,电荷运动停止,则该电场随即消失。更精确的证明应综合考虑以下三点:1).运动电荷本身所产生的磁场是沿电荷径向递减的。2).变化的磁场在其周围产生感生电场。3).如果电荷的运动成分没有完全转化为磁场的话,则还需考虑含有电荷运动分量的“R物质”微粒与电荷周围磁场的作用。
4. 变化的电场激发感生磁场的解释见说明5。
5. 变化的磁场激发感生电场的证明见说明7。
磁场部分的证明到此为止。
第三部分:重力场
重力场是由大量“R物质”微粒作低速直线运动而形成的。所谓低速是相对于电场中“R物质”运动的平均速率而言的。也就是说,重力场中“R物质”运动的平均速率远远小于电场中“R物质”运动的平均速率。实际的重力场是含有波动成分的,也就是说,实际重力场可分解为波动成分和重力场成分。重力场是大量“R物质”微粒运动的集体表现。重力场是源于星球的。
1.对“R物质”不断地低速发射或吸收形成了星球的场。
恒星不断地低速发射“R物质”,而行星不断地低速吸收“R物质”。当恒星和行星相互靠近时就会相互吸引,即产生了引力。星球的形成见说明1。
| 2.实际重力场的简化。 在实际重力场中,“R物质”的运动具有如下特点:1).“R物质”的运动是靠微粒间的多级碰撞而进行的。2).“R物质”的运动既含有波动的成分又含有直线运动的成分,其中直线运动的成分就是重力场,而重力场中微粒之间并不发生碰撞作用。因此,实际重力场是波动成分和重力场成分的叠加。在实际重力场中,要研究某一区域“R物质”微粒的平均速率或平均密度的话,在波动成分能量远大于直线运动成分能量的条件下,可以忽略波动成分。实际重力场的直线运动成分(即:重力场)如图3-1和图3-2所示。在图3-1和图3-2中,“R物质”微粒之间并不发生碰撞作用,且微粒沿图示箭头方向作匀速直线运动,而且微粒运动的平均速率远远小于电场中微粒运动的平均速率。图中“R物质”微粒 |
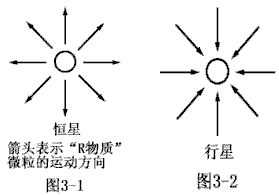 |
| 的位置和能量是沿径向空间均匀分布的。沿径向空间均匀分布是指如图3-3所示。即沿径向空间的任一截面中,微粒的数目和微粒运动的平均速率都相同,且沿径向空间的任一截面中,微粒都是均匀分布的。 3.星球的受力规律。 若星球两侧区域的“R物质”平均密度不相同,则星球将受到力的作用,力的方向是指向平均密度小的一方(星球受力规律的证明见说明8)。 4.星球之间产生力的原因。 为了描述星球发射或吸收“R物质”的能力,把单位时间内星球发射或吸收的“R物质”微粒数目定义为星量。 |
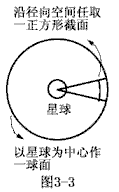 |
| 先从恒星和行星谈起,为了叙述方便,设一恒星和一行星的星量相等,如图3-4所示。由于恒星所发射的“R物质”微粒全部由行星所吸收,也就是说,就重力场中的某一微粒而言,它既属于恒星所发射的同时也属于行星要吸收的,因此可利用叠加原理。叠加的结果是,两星球之间的内侧区域中“R物质”运动的平均速率增大了,平均速率增大是相对于两星球单独存在时的情况。而两星球的外侧区域中“R物质”运动的平 | 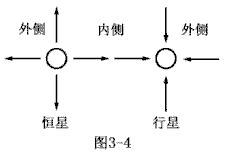 |
均速率减小了。根据密度分布规律,两星球之间的内侧区域“R物质”的平均密度应小于其外侧区域“R物质”的平均密度。根据星球受力规律,两星球均应受到指向内侧的力,因此,恒星和行星就表现为相互吸引,即产生了引力。请注意,以上推导是在恒星发射“R物质”的速率等于行星吸收“R物质”的速率的情况下。如果行星吸收“R物质”的能力极差,则星球两侧由速率差而引起的密度差就很小,因而它们之间的引力就不明显,甚至表现为斥力。行星吸收“R物质”能力的大小主要受以下因素的影响,1).恒星所发出的波的强度和波的频率的影响,即波的强度越大,频率越高,则行星吸收“R物质”的能力越强。2).行星本身体积大小的影响,即行星的体积越大,则它吸收“R物质”的能力也越强。
在恒星发射“R物质”的能力和行星吸收“R物质”的能力大致相当的情况下,则表现为同性星球相斥而异性星球相吸。需要说明的是恒星之间是无条件的相斥,而行星之间则是有条件的相斥。
同性星球相斥的证明方法和上述方法大同小异。现仅就证明结果介绍如下:同性星球之间产生斥力的原因是由于其内侧区域“R物质”的平均密度大于其外侧区域“R物质”的平均密度,因此星球将受到指向外侧的力,即表现为相互排斥。
因此,星球之间的力是它们的重力场相互作用而产生的。
5.物体受到重力的原因。
物体是由原子或分子构成的,而原子是由正负电荷构成的。那末电荷和星球有什么关系呢?恒星和正电荷很相似,而行星和负电荷也很相似,那么恒星和负电荷之间是否能构成发射和吸收“R物质”的关系呢?其实,恒星所发出波的频率要在一定范围内,恒星和行星之间才能构成发射和吸收“R物质”的关系。同样,正电核所发出波的频率也要在一定范围内,正电荷和负电荷之间才能构成发射和吸收“R物质”的关系。但这两个频率范围相差太大,因此恒星和负电荷之间是不能构成发射和吸收“R物质”的关系的,也就是说,恒星和负电荷是不能形成相互吸引的。以上是从波的角度来分析电荷和星球的关系的。下面来分析一下电荷处在重
| 力场中的受力情况,如图3-5所示。由于在电荷周围形成电场的“R物质”运动的平均速率远远大于形成重力场的“R物质”运动的平均速率,因此就相对于形成电场的“R物质”运动的平均速率而言,形成重力场的“R物质”的低速运动状态就相当于静止状态(简称静态)。因此在电荷电场的作用范围之内,形成电场的“R物质”运动的平均速率基本上不受重力场的影响或重力场对电荷电场的影响也仅是对称性的。因此在电荷的上下两侧区域中,“R物质”运动的平均速率基本上相等,因此由电荷两侧“R物质”运动的平均速率差而引起的平均密度差近似为零。然而形成重力场的那些“R物质”却在连续不断地发生静态位移。这种静态位移连续不断地使电荷上侧区域“R物质”的平均密度增大,从而使电荷上下两侧区域的平均密度差持续增大。当这种密度差达到一定程度时,根据电荷受力规律,电荷将在重力的作用下而产生位移。也就是说,形成重力场的“R物质”,由于其平均运动速率很低而基本上影响不了电荷周围“R物质”的速率分布或也仅对速率分布产生对称性的影响,但由低速运动而引起的位移却连续不断地在电荷一侧积累“R物质”而使电荷两侧产生密度差。 | 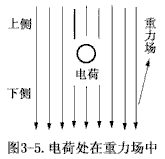 |
由以上分析可知,静止电荷在重力场中是受到重力作用的,但由于重力的作用过程是一种低速过程,因此,如果电荷的运动速度很高,则可忽略重力对它的作用。
由于物体中大量的原子或分子在不停地振动,可把物体中原子或分子的运动分解为静态分量和振动分量。因此处在重力场中的物体受到重力场的作用实质上是指重力场对物体中原子或分子静态分量的作用,从而使物体受到重力的作用。由于形成重力场的“R物质”运动的平均速率很低,因此物体所受到的重力是不可能引起物体的高速运动的。
从物体和星球的受力原因上来看,物体和星球是不同的。物体虽为星球的一部分,但孤立的物体周围是不存在重力场的;也就是说孤立的物体再大,其周围也不会有重力场,而孤立的星球周围是存在重力场的。因此,重力场是区分物体和星球的重要标志。星球之间的力是它们的重力场相互作用而产生的,而物体在重力场中受到的力是重力场作用于物体而产生的。我们知道,万有引力理论在受力分析时,把物体和星球混为一谈,认为万物皆存在着引力,但至今也无人能说清万有引力的产生原因。
请注意,物体在重力场中所受力的方向是沿重力场方向的。由于太阳重力场的方向是发散的,而地球重力场的方向是收敛的,因此,当物体接近太阳时,它将受到太阳的排斥,而当物体接近地球时,它将受到地球的吸引(这两种情况的验证见说明9)。
6.月球和地球之间产生引力的原因。
月球和地球随都属于行星,但它们吸收“R物质”的能力却有很大差别。形成月球重力场的“R物质”运动的平均速率远小于形成地球重力场的“R物质”运动的平均速率。设形成月球重力场的“R物质”运动的平均速率为![]() ,形成地球重力场的“R物质”运动的平均速率为
,形成地球重力场的“R物质”运动的平均速率为![]() (“<<”表示远小于的意思),因而有
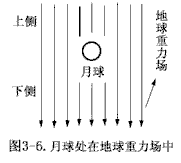
(“<<”表示远小于的意思),因而有![]() 而言,形成月球重力场的“R物质”的运动状态就相当于静态。因此,如果把月球放在地球的重力场时,如图3-6所示。
而言,形成月球重力场的“R物质”的运动状态就相当于静态。因此,如果把月球放在地球的重力场时,如图3-6所示。
| 由于形成月球重力场的“R物质”的运动状态近似为静态,因此月球在地球重力场的作用下,其上侧区域的“R物质”不断地积累,从而使其上侧区域“R物质”的平均密度大于其下侧区域“R物质”的平均密度,根据星球的受力规律,月球将受到指向地球方向的引力的作用,因此月球就表现为受到了地球的吸引。请注意,月球和太阳之间并不存在引力的关系。万有引力理论就是在这上面出了问题。按万有引力公式计算,太阳和月球之间的引力大于地球和月球之间的引力,也就是说,和地球相比,太阳吸引月球的力更大。那么,月球为何不围绕太阳而是围绕地球转呢?显然,万有引力理论不能自圆其说。需要说明的是,月球受到了地球引力,而物体也受到了地球引力,这两个力是有区别的(详情见说明1)。
重力场部分的证明到此为止。 |
 |
作者:芦光耀. 日期:2005年5月11日. 电话(Tel):68751647.
身份证号码:110106196311223313
住址:北京市丰台区东高地三角地37栋丁门四楼111号。
邮政编码:100076
E-mail:hulahuaer@hotmail.com
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑