物理科学探疑-网友天空-空间与介质-空间基本能量转换中的热力学规律——关于暗物质和暗能量的讨论
空间基本能量转换中的热力学规律
——关于暗物质和暗能量的讨论
（高连全）
摘要：本文从
介子衰变为光子出发，提出空间基本能量的概念，指出这是一种新的能量转换形式并推导出了空间基本能量与质量之间的质空当量关系式。在确定空间物质性的基础上，从真空的量子“涨落”出发，运用热力学的一些原理推导出空间基本能量匀态聚集的结构、密度和质量以及形成条件等，根据匀态聚集与暗物质的相同特性，认定它就是暗物质。并指出一切由静质量不为0的实体粒子构成的物质是以带分数电荷的夸克为核心的空间不均匀聚集，引力子是一个多余的概念。指出空间能量的三种形态分别对应于粒子物质、暗物质和暗能量。并据此讨论了它们之间的引力关系，解释了为什么恒星—行星系内适用的是万有引力、星系内引力的不规则性、星系之间的斥力以及宇宙的阶段性暴胀的原因。
关键词：介子衰变，空间基本能量，能量聚集，质空当量，暗物质和暗能量，引力关系。
第一部分：关于空间基本能量概念的提出
一、关于能量转换的一种新的形式
能量转换是人类最早认识的规律之一。在现实世界和实验室中，粒子之间的互相转换是十分常见的。中性
介子在系统中的能量是
，为简便起见，我们可以选取一个参照系，使
介子在其中的相对速度为0，那么，
介子的静能量写为：
(1-1)
现在我们考察一下它的衰变过程：在一个系统中，中性的
介子的平均寿命约为
秒，之后衰变成两个
光子，这一过程的能量转换关系早已为科学前辈所论证，是大家熟悉的质能转换关系，用方程式表示为：
(1-2)
衰变后每一个
光子在空间传播的能量是
，写为：
(1-3)
上式也可以理解为：衰变后的光子携带数值为
或
的能量在空间传播。
以上的结论是人所共知的，现在我们想问的问题是：衰变后的光子能量是
或
、速度是
，在纯粹的理论上、在没有任何干扰的情况下，这个在光子的传播在时间是永久的吗？或者说它在空间上传播是无限的吗？
如果它是在时间是永久、空间上无限的，说明
光子是
衰变后的最终形式，即它不再发生其它形式的能量转换。现在，我们来论证它的传播在空间不是永久的、在空间上也不是无限的。用反证法：
A
← ○ →
光子1
光子2
B
－∞←………………… …………………→＋∞
←
光子1
光子2→
C
－∞……………………………→
←……………………………＋∞
光子传播的T反演
D
－∞…………→ ←…………＋∞
光子传播的T反演
（图一）
介子衰变成的两个
光子，它们必然是反向而等值的(如图一A)。假设它是永远传播的，那么它传播的传播距离终点是“无穷远点”±∞
(如图一B)，这是个不可计数的量，它存在的时间也就是“无穷大”∞，也是不可计数的。那么，现在我们对这一过程实施T反演。我们已知，衰变主要是弱相互作用的过程，根据弱相互作用中T反演不守恒的原理，反演操作的光子出发点就不应是原光子的“传播距离终点是“无穷远点”∞”，而应该是±∞’。这个±∞’点要么在“无穷远点”±∞之前，即比“无穷远点”±∞更远(如图一C)；要么在“无穷远点”
±∞之后，即比“无穷远点”±∞近一些(如图一D)，那么，“无穷远点”
±∞点就不是无穷远的，而是一个可以计量的点。因此，衰变后的光子在空间传播的距离是有限的，它在时间上也是可以计量的。
介子衰变成
光子后，
光子在空间传播一段距离消失，它最初的能量形式是粒子（数值是
），转化为
光子后能量形式是光子或者说是电磁波、电磁场（数值是
），当它在空间消失后，组成其能量
都没有了，那么它到哪儿去了呢？在这一过程中，与能量
相伴的只有它存在的这段时间
和它所通过的空间
了，如果不是认为它消亡了的话，那么只能认为它存在于它存在的这段时间
和它所通过的空间
了，也可以说它转化为它存在的这段时间
和它所通过的空间
的了，换句话说，它从拥有频率为
、波长为
的光子（电磁波\电磁场）转化为拥有时间
、和空间
的空时了，或者说，它转换为占有了具有时间维
、空间维
的的空时。借助二维空间和三维空间中的概念，占有一个平面和立体空间分别用
表示,
那么，具有能量
的光子就转化为时间
和空间
（占有了具有时间维
、空间维
的的空时）乘积了，表示为：
简写成
，我们将这种新引进的能量形式命名为“空间基本能量”，简称为“基本能”，用字母
表示，即：
（1-4）
二、关于空能转换的关系
既然空间也是一种能量形式，根据爱因斯坦的质能等效性，空间与能量之间的转换关系在数值上也应当是可以确定的值，它们之间也应该存在着类似于热力学中“热功当量”关系的质空当量关系。现在仍以上面在
介子衰变为例。
由于光速不变原理，
光子的速度必定是
。因为
，所以
(2-1)
那么，式（1-4）可以写成：
（2-2）
从光子
转换为基本能的过程可以表示为：
(2-3)
并变化为：
（2-4）
（2-5）
式（2-4）和（2-5）就是静质量为0的粒子在频率为
时与空间基本能量相互转换的一般关系式。
在确认能量守恒的前提下，我们已知：在
介子衰变为2个
光子后，又相应地转换为空间基本能量。那么，
介子与空间基本能量的关系是两倍关系。即：
（2-6）
将（2-2）式代入（2-6）式，得：
（2-7）
（2-8）
去掉上式中的下标，并将2改为i，就得到一般粒子转变为i个光子时，其中一个光子的线空间能量：
（2-9）
对于（2-8）式所表示的中性
介子与空间基本能量转换的关系式，我们已知光速为
，电子质量
，中性
介子质量约为电子的264.3倍，那么中性
介的质量为：
（2-10）
将光速和（2-10）式数据代入（2-8）式，得：
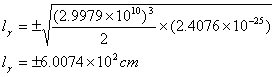（2-11）
式（2-10）就是
介子衰变后的两个光子之一在空间存在的线空间长度。
现在来讨论与
介子等价的空间能量数值。
由于光子是无质量的，因此，它可以转变为线空间。而
介子本身是有质量的也有体积的，与它等效的空间能量就不应该是线空间，而是体空间。由于
介子在衰变时是同时产生两个光子，这两个光子必定是动量相等，方向相反的，而且，两个光子在任一方向上都是可能的、相同的，因此，表示
介子存在的空间应当是以（2-11）值（一个光子存在的线空间长度）为半径的球体，已知球体的体积公式是：
（2-12）
上式中
是圆周率，R是球体的半径。那么
介子转变为空间基本能量的值是：
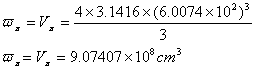(2-13)
从（2-11）和（2-12）式，我们得到粒子和空间基本能量相互转变的质空当量关系式：
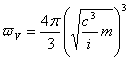（2-14）
是粒子的三维空间基本能量的值；
是圆周率；
是光速；
是粒子转变为光子的个数；
是粒子的静质量。
（2-10）和（2-13）都是中性
介子所蕴含的能量的，是用不同概念描述同一对象的同一性质的，因而两者必定相等，那么，就可折算出粒子质量与空间基本能量的一般换算关系值是：
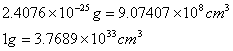（2-15）
上式的倒数就是宇宙中空间基本能量的密度：
（2-16）
我们已知目前宇宙的平均密度是：
（2-17）
空间能量的密度比宇宙总密度小2个数量级，宇宙总密度是空间能量密度的大约200倍，这个值在逻辑上是合理的。
第二部分：关于空间能量转换中的热力学原理
三、空间基本能量的匀态聚集结构
在我们目前已知的来看，暗物质是自身不发射粒子，也不吸收、不反射粒子，只能通过其对周围物体的引力作用知道它的存在。它是如何产生的？它的结构如何？它为何有上述特点？等等一系列问题，我们只能从已知的现象去讨论：
1、空间能量转换成匀态聚集的过程
现代观测证明，真空中不是静止不动的，也不是永远都一无所有的，它其中一刻不停地产生着“量子涨落”，不断出现虚粒子，即成对地产生正反电子对旋即化为光子湮灭，这是空间能量物性的体现。
考虑在一个固定的区域内，产生“量子涨落”的条件是一定的，在一定时间内出现正反电子并转化为光子的概率是P1，众多的光子发生碰撞的概率为P2，在这众多的碰撞中，由于其光子的能量不是很大，不可能再产生新的粒子，这当中发生如图正碰撞的概率是P3（两个粒子处于同一空间直线上，对头相遇时处于同一能级）。当两个能量相同的光子作正碰撞时，不会发生散射，只会形成一种处于静止的平衡状态的光子对，当然也可能是几个光子处于平衡态而形成的光子团。形成光子对或光子团的概率是：
（3-1）
这些光子对或光子团它们之间的距离应该是波长的整数倍。周边未参与正碰撞的光子转化为空间基本能量，剩下了一些处于静态平衡的光子对或团，它们组成的蜂窝状的物质是一种新的物质形式。
处于静态平衡的光子对或团必定是在“量子涨落”产生的光子在湮灭前形成的，它与空间基本能量的能量密谋的比较可用图二表示，图二之A是①②形成光子对的能量情况；B是光子①的全部线空间基本能量；C是光子②的全部线空间基本能量；D是光子①和②的全部线空间基本能量之和。从图中可以算出：由光子对或光子团组成的新物质的最低密度大于空间基本能量的密度，应该把它看成空间基本能量的一种聚集，并且由于它没有组成核心而是形成了一个个相互联系的质点，因此称它为匀态聚集。
（图二）
我们知道热力学中熵的概念意义是热量被温度除的商，外文原名的意义是转变，指热量转变为功的本领。通过前面的讨论，应当认识到，从空间能量到匀态聚积也是一个能量转换过程，我们现将熵的概念推广到这一过程中，意义为质量被能量除的商，指能量转变为引力质量的本领，符号也用大写的拉丁文字母
。那么，可以表示为：
（3-2）
事实上，在少量的光子对或光子团（为简便以下统称光子团）形成时，由于外界的扰动，组成光子团的光子会从团中逸出，重新化为空间基本能量，因此，这这种情况下，空间基本能量形成光子的过程是一种可逆过程。从热力学知，在可逆过程中，熵不变，即S=0；在不可逆过程中，熵增加，即S＞0。
因此，在可逆过程中：
（3-3）
对于一定区域内的空间基本能量
，当S值足够大时（大于临界速率），众多处于处于平衡状态的光子应付账款产生引力作用，引力加速了周围真空的涨落，P1增大，相应地导致
的值增大，在同一区域中，新形成的光子团的数量大于因扰动而消失的数量，这时，我们令：
（3-4）
即：
（3-5）
我们称
为临界概率，
为临界熵。
从（3-4）式出发，当时
时，使这形成光子团这一状态成为不可逆的过程，系统的熵增大，
，能量匀态聚集越来越多，对外表现出一定的引力作用，形成物质块，随着它的引力质量也越来越大，根据相对论，其周围相邻区域引力越来越强，时间越来越慢，从（3-5）式可知，决定
值的不是时间
而是时间的三次方
，因此，
越来越小时,
更迅速地减小，最终达到：
（3-6）
此时，该物质团不再生长。
2、新物质的表现形式
从上面的讨论我们知道，由光子团组成的新物质，它任意一部分的成分相同，结构相同，因而其内部是各向同性，受力均匀的，不会向某一点塌缩，也就不会形成规则的星体，它只对外表现出引力作用。由于它是由纯光子组成的稳定结构，它在形成的急剧成长阶段量子涨落产生的正负电子数量暴涨，会有很多P值虽然很大，但仍不可能是100%，仍有大量未参与形成光子团的光子向空间逸出，对外放出大量的光子，一旦稳定后，它对外不发射光子。
在讨论物体与其它物质特别是电磁波（光子）的互相作用时，阻止本领z是个常用的概念，它是指入射光子在阻止物质中行径单位长度时的能量损失。
对于光子团，不论它是由几个光子组成的，它总是处于稳定的振动状态，如图三，假设光子团是由①②③三个光子组成的，入射光子④进入光子团后它的路线与通过③所处的位置，由于光子的波动性，若③与④频率不同，④将绕过③继续前行，该光子团对于④来说是透明的；若③与④频率相同，入射光子④将占据③的位置代替③与①②重新组成稳定的光子团，而光子③离开光子团形成运动状态，由于动量不变的原理，运动后的光子③，将沿光子④的前行方向，并保持光子④的频率，由于光子的能量是由频率决定的，而且，因为光速不变的原因，③和④方向一致、频率相同、能量相等。
因此，不管何种情况，光或其它任何波段的电磁波入射暗物质时的强度和射出时的强度是一样的，即新物质的阻止本领是：
Z=0
（3-7）
因此，从它对其它物体有引力作用，但自身不发任何电磁波（光子），也不反射、不吸收任何电磁波（光子），可以断定它就是用电磁波是无法探测的暗物质。
3、空间基本能量转换成匀态聚集的条件
从开始有暗物质生成时的到形成稳定的暗物质团的过程，可以表示为：
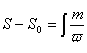（3-8）
在上述过程中，从热力学原理可知，在没有外来质量的情况下，熵是非负的，我们设
，同时考虑，在（4-2）式中右边的积分号中，空间能量
是聚集的源头，
是聚积的成果，因此，可将
看作积分自变量，上式化为：
（3-9）
解得：
（3-10）
我们已知，积分常数C是由系统的初始条件决定的，因此，在初始条件确定的情况下，我们可以不考虑积分常数。因而（4-4）式简化为：
（3-11）
从上式知，真空“涨落”是否会形成暗物质的条件是由空间能量的自然对数确定。当空间基本能量数值等于“1”时，S=0，真空“涨落”中形成光子团是可逆过程，不会形成暗物质。当空间基本能量能量的数值大于“1”时，S＞0，真空“涨落”中形成光子团是不可逆过程，将形成暗物质。在这里，我们将空间能量“1”的值称为空间匀态聚集阀值。
4、空间能量匀态聚集的结构、密度和质量
上文已经讨论过，暗物质是由正碰撞的光子对在稳定状态下形成的，这两个粒子处于同一空间直线上，在这条直线上，能量就集中在这一点，其它点的能量为0，这恰好满足狄拉克的
函数的条件，现来具体讨论：
用
来表示线空间的能量密度，它满足：
（3-12）
上式
函数的积分表示集中的能量：
（3-13）
表示所有的能量均集中在一点。
位于区域
点的能量是2个光子组成的质点，它的质量表示为：
或者简写为
对于已经稳定的成块状的暗物质，可以把它看成许多质点的累计，它的质量表示为：
暗物质的一维密度和结构可以用
函数的傅利叶积分表示：
（3-14）
上式中
是不连续的参数，它跳跃式地依次取值
且无限增大，
每次跳跃的增量是
，在此可以理解为光子团间的平均距离。暗物质就是由等距离的光子团组成的，这样暗物质的在一维上的引力质量就是：
（3-15）
M是暗物质的线质量，a、b是暗物质存在的线空间区间，w是光子团之间的平均距离。
当然，也可能是三个、四个甚至是多个光子碰撞在一起形成的平衡态的光子团，很自然地将
函数推广到三维：
（3-16）
从上式可知：
（3-17）
可以简写为：
（3-18）
四、空间基本能量的有核聚集方式
通过上面讨论可知：空间也是一种能量形式，而且是最基本的能量形式，这种能量均匀聚集形成了一种新的能量形式，由于新能量形式不能被电磁波（光子）探测，因此被称为暗物质。空间和暗物质这两种能量形式的共同点就是它们在能量分布的结构上是均匀的，没有占据能量主要部分的核心。而以粒子为代表的各种可见物质，无论是星系一样宇观的系统还是原子一样微观粒子都有质量核心。因此，可以认为：可见物质是能量的有核聚集。这部分能量具有实物粒子的一切特征，它能发射、吸收和反射粒子。它的运动规律遵循牛顿力学，它在大量聚积的宇宙尺度上符合广义相对论的规律，在个别个体状态下符合量子力学的要求。这就是我们现在科学理论研究最多的物理学的研究对象。
形成实物粒子的核心是什么呢？现在科学普遍认为带分数电荷的夸克是基本单元。因此，应该认为，几个不同的分数电荷相聚时，形成一个整数电荷，该电荷产生了一个微小的电场，破坏了空间基本能量的平衡和各向同性，均匀的空间被扭曲，产生了万有引力，形成能量的有核聚集。
五、引入空间基本能量后的物体受力关系
上面讨论了能量的三种物质形态：空间基本能量、暗物质、实物粒子。对于它们可以借用势力学的概念加以讨论
对于体系中只有一种能量形式的称为单相系，同时有二、三种能量形式的称为二相系、三相系或统称为多相系。
1、粒子（物质）单相系的受力情况
在任意一个星系中，星系核心以外的周围的任意一个星体（气体云、尘埃）绕核心作圆周运动。这个一个星体（气体云、尘埃）同时受核心的的万有引力（向心力）和圆周离心力。因为物体在作圆周运动时,向心力与离心力的大小是相等的。
星体受到的的万有引力是：
（5-1）
式中G引力常数，M为星云的质量，m是星体的质量，r是物体离中心的距离。
星体作圆周运动时的离心力是：
（5-2）
r是物体离中心的距离，v是物体的线速度，m是物体的质量。
星体所受的的万有引力应跟离心力相平衡，即
，等式两边消去m，于是有：
（5-3）
等式左边是重力加速度,右边是圆周运动的向心加速度。简化并变形得：
（5-4）
由于引力常数G和星云质量M都是常数，由以上公式可以看出，恒星线速度v的平方和星体离星云中心的距离r成反比。于是，星体离星云中心越远，其线速度就越小。
2、暗物质单相系的受力情况
现在来考察对暗物质的万有引力：从以往的实践和经验来看，牛顿的万有引力定律只对可以看作质点的互相作用是被充分检验的，在大尺度这一定律是否有效则未经检验。
（图四）资料图片：科学家绘制出的宇宙暗物质三维数字地图
从上图可以看出，暗物质是呈不规则的团块状，空间体积十分巨大
。与大质量的恒星或星团不同，即使在星系和星系团的尺度，它也不能被看作质点，但我们可以取其中的一个微小单位
看作质点，而每个质点是符合万有引力定律的，
所受的万有引力为：
式中G引力常数，M为星云的质量，m是暗物质微小单位的质量，
是这个微小单位距引力中心的距离。
整块暗物质所受的引力就可以看作对
的积分，考虑暗物质存在的范围，a是离引力中心最近的点，b是离引力中心最远的点，那么就可以用定积分来表示：
（5-5）
（5-6）
根据中值定理（5-5）式可解为：
（5-7）
（5-8）
对（5-6）式，还可以根据牛顿-莱布尼兹公式可解为：
（5-9）
（5-10）
比较（5-7）式和（5-9）式，可知：
（5-11）
解为：
（5-12）
从上面的讨论可以看出，b-a表示暗物质块的径向长度，为简便起见，令b-a=d，则（5-7）式和（5-9）式可简化为：
（5-13）
3、空间基本能量单相系的受力情况
由于空间基本能量不是能量的聚积方式，没有明显的边界，更不能看作质点，所有的物质和暗物质都处于空间基本能量之中，因些，也不能用带有积分区间的定积分计算，但可以设定其中的一小部分为质点，用不定积分来讨论：
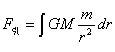（5-14）
在上式中对r求积分时，G、M、m都可以看作常数，故上式可变为：
（5-15）
求出（5-14）式的原函数是：
（5-16）
这是一个负数。它意味着，一个引力中心与没有边界的空间基本能量相作用时两者之间不是引力而是斥力。
现在回到定义空间基本能量的（1-4）式，可以知道，空间基本能量就是一般的空间，它不发光，也不吸收、不反射光线，而与实物粒子之间的互相作用是斥力。因此，可以认为空间基本能量就是推动宇宙膨胀的暗能量。
4、多相系的受力情况
考虑到在实际的状况下，空间能量是无所不在的，暗物质往往是伴随星体存在的，而星体是可以看作质点的，因此，我们在讨论物体间的受力时，其实上述三种情形是同时存在的。我们已知，引力是可以叠加的，因此，实际空间中两个物体A和B之间的受力关系应当表示为：
（5-17）
上式中，
表示引力，
是引力常数，
是系统的引力核心，
是暗物质的质量，
是空间基本能量等价的质量。
整理为：
（5-18）
从(5-18)式可以看出，两物体间的引力关系是正还是负，取决于体系中三种能量形式的比例，以及它们与引力核心的距离。在（5-18）式中，右边第一项是星体的质量；第二项是暗物质与其分布空间大小的积；第三项是空间基本能量（暗能量）与星体到引力核心的距离之积。
在象太阳系这样恒星行星系的尺度内，第二项较小，第三项更小，起主要作用的是第一项，因而遵循牛顿万有引力定律；在银河系仙女系这样恒星组成的系统中，由于有大量的暗物质存在，第一项第二项共同起作用，第三项仍然较小，物体之间表现的仍以引力为主；在大的星系之间，由于距离十分遥远，因此，距离
和空间基本能量（暗能量）
的值比较大，第三项斥力的值超过了前两项引力之和，因此，物体间的互相作用表现为斥力。
在本文的前面讨论暗物质形成条件时，给出了（3-10）式，对该式的物理意义是：在初始条件确定的情况下，当空间能量大于阀值时，会有暗物质形成。因为暗物质是由空间基本能量（暗能量）转变而来的。因此，在一定的范围内，当暗物质开始大量形成时，在（5-18）式中，第三项的负值项
减小，所减小的量转变为第二项正值项
，物体间互相作用中，表现为引力的趋势增强、斥力趋势减缓，宇宙膨胀速度减慢。当暗物质形成到达一定的规模，因其引力增大、时间膨胀，（3-5）式中的T持续减小，最终达到（3-6）式的条件，此时，暗物质产生的速率减小，物体间互相作用中，表现为斥力的趋势增强、引力趋势减缓，宇宙膨胀速度加快。由此我们能得到一个推论：宇宙膨胀和暗物质的形成是交替产生的。
5、不同相系受力之间的数学联系
上述对星体、暗物质、空间能量三种受力情况讨论的数学模型是有联系的。以（5-17）式为例，等式右边三项之间是可以互相推导的。
对（5-16）式，它虽然是负值，但它是由不定积分（5-15）推导的，根据不定积分的原函数族定理，相对应的原函数族应为：
(5-19)
C是原函数族的任意常数。热力学、电磁学和力学中的积分常数都是由体系内的初始条件决定的。因此，也可以认为，（5-19）式中的C是由物质产生时的初始条件决定的。
从（5-19）式可以看出，考虑原函数族常数在内时，G、M、m都是正的，所以引力F引的正负由括号内的结果决定，而且r不可能为负，综上所述可得：
（5-20）
从数学角度看，（5-19）式可以简化为幂函数的标准形式：
（5-21）
（5-21）式的原函数簇用函数图象表示为：
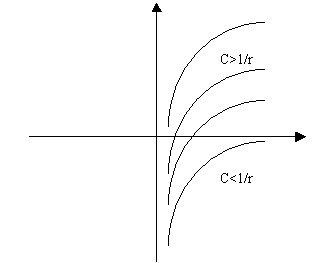
（图五），距离和引力关系函数图簇
(5-20)式的意义应这样理解：对任何一个体系而言，其初始条件只能有一个，而且其是定值，我们设定D=1/r。当两物质初始距离大于D时，它们之间的作用力是引力；当两物质初始距离等于D时，它们之间的引力为0；当两物质初始距离小于D时，它们之间的作用力是斥力。根据现行的宇宙大爆炸理论，在宇宙大爆炸的同时产生了空间，空间相互之间的初始距离≤D，因此暗物质之间的作用是斥力；实物粒子和暗物质是在宇宙大爆炸之后产生的，它们之间的初始距离＞D，因此，实物粒子和暗物质之间的作用是引力。
即从第三项推导出第一、二项。
对于（5-19）式，由于必须保持量纲的统一性，所以，积分常数C必定可写成
的形式，因此，（5-19）可变化为
（5-22）
比较（5-22）和（5-9）可知，两式是相同的。
即从第三项推导出第二项。
对（5-5）式所表示的定积分，积分区间不同时，结果也不一样。
Ⅰ、当
时（
是极小数），即积分区间数值很小但大于0时，
讨论的对象可以看作质点，那么，（5-5）式就还原为牛顿万有引力
。
即从第二项推导出第一项。
Ⅱ、当
时，
（5-5）式
就可以看作是不定积分（5-11）
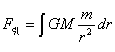，它的原函数是式（5-16）：
。
即从第二项推导出第三项。
Ⅲ、当
时，
此时讨论的情况比较复杂，应分别讨论：
在星际内，相对于实物粒子和暗物质，空间能量的数值较小，从（2-14）和（2-15）可知宇宙中空间能量的平均密度比宇宙平均密度低两个数量级，在物质聚积的星系或星系团内，可以确定物体的积分区间，即空间（暗能量）是可以忽略的，但在当大于星系（星系团）内部尺度，在星际长城尺度内，由于星系相距十分遥远，两地之间积累的空间（暗能量）巨大，达到与两者的质量在同一个数量级，那么，这时两者之间的互相作用则不能忽略它的存在。因此，在天文学家已观测过的967个星系（包括银河系）都显示出的引力异常——远离星系中心的物质的速度不随距离的增大而减少，就如同远离星系中心的物质的运动不受牛顿引力的约束一样。恒星的线速度是分段的曲线，如图六，仙女星系周边恒星的速度和它们与星系中心距离关系的曲线，随距离的增大速度并不下降而是出现平坦化。
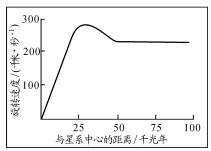（图六）、
仙女星系恒星速度和它们与星系中心距离关系
对于这种异常情况，如果用（5-18）式所表示的引力关系来讨论，对于确定的恒星B其离心力和引力平衡表示为：
（5-23）
化简为：
（5-24）
从（5-24）可知，对于确定的恒星B，
这几个值都是定值，因此，决定速度
异常的就是暗物质质量
和它的分布距离
。前文讨论过，暗物质是空间基本能量（暗能量）的匀态聚集形式，因此，它不会大量存在于粒子物质很多的地方，否则，粒子物质会破坏它的各向同性与均匀性，因而，它必定主要存在于粒子物质不多的星系外围。在星系外围的恒星实际受到的引力作用比单纯星系核心的万有引力要大，恒星必须具有更大的速度才能保持离心力与引力的平稳，越往远处，暗物质越多，这种效应越明显，因此，速度曲线出现平坦化。
结论：
1、本文提出空间是能量的基本形式，导出了质空当量关系式：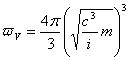
和计算值
以及空间基本能量的密度：
；
2、空间的匀态聚集形成暗物质，它的质量为
；
3、两物体间的引力关系是：
参考文献：
1、《数学物理方法》，梁昆淼编，人民教育出版社，1978年8月，第二版；
2、《热力学简程》，王竹溪著，人民教育出版社，1969年8月，第一版；
3、《统计物理方法（修订本）》，陈仁烈编著，高等教育出版社，1978年12月，第二版；
4、《经典和近代物理学》，K.W.Ford,陈纲译，高等教育出版社，1983年，第一版；
5、《物理之谜》，杨宗书编，文汇出版社，1990年，第一版。
版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明 © Copyright Authors
物理科学探疑