物理科学探疑-网友天空-关于技术-能源的存亡

能 源 的 存 亡

沈建平

能够自行产生能量的永动机是不存在的，能量是只能从一种形式转换到另一种形式。那么，动态磁路一、动态磁路二也许就打破了这种观点。

    早在两千多年前，人们就已经发现了磁现象，但长期把它孤立地看做是某种物质所具有的特殊性质，由于对它的认识不深，应用也不广泛。随着科学技术的发展，先后发现了电流的磁场和磁场对电流相互作用的关系，从而大大地扩大了它的应用范围。本稿是对磁场应用领域的又一次探索。

一、    磁现象的基本知识

    1、磁体：有天然磁体、人造磁体。

    能够长期保持磁性的磁体叫做永磁体，天然磁体和人造磁体都是永磁体。使原来不具磁性的物体得到磁性叫做磁化，使磁体失去磁性叫做去磁。

    2、 磁极：把一根条形磁铁放到铁屑里再拿出来，我们可以看到它能吸起很多的铁屑，吸引铁屑最多的地方磁性最强,称为磁极。条形磁体和磁针的两端都是磁极，把一根条形磁铁悬挂起来，指向北方的磁极叫做北极用N表示，指向南方的磁极叫做南极,用S表示。两个N极或S极相斥，N极与S极相吸。

    若把一磁棒折成两段，那么在折断处就会出现了两个异号磁极，因而每一段又都变成了具有南北两极的磁棒。再分下去，每一小段又都具有南、北两极;继续分割下去情况总是如此,每一小段总是一根完全的磁体。

    3、 磁感应：用一个磁体靠近软铁棒，虽然磁体没有和软铁棒接触，这时软铁棒有了磁性，软铁棒有了磁性，我们说它磁化了，软铁棒在磁体附近被磁化的现象叫做磁感应.。用磁铁的N极靠近软铁棒,软铁棒被磁化S极，远离磁铁的一端为N极。磁铁取走，已被磁化的软铁棒的磁性也消失，如果被磁化的是钢棒，当磁铁取走后，钢棒上仍保留有磁性。

    4、铁磁性材料：软铁和钢是能够被磁化的材料，我们称它们为铁磁性材料。铁磁性材料有的是金属，也有的是非金属。铁、镰、钻等属于金属的铁磁性材料，它们又可分为两种,一种如碳钢、钩钢、铝镣钻的合金等，一经磁化，磁性不易消失，这种材料叫做硬磁性材料。永磁铁就是用硬磁性材料制成的。另一种如软铁、硅钢、坡莫合金(镍铁合金)等,它们在磁化后，磁性容易消失，这种材料叫做软磁性材料。其中硅钢是制造电机、变压器等电器铁芯的重要材料。

    5、 磁场：磁体周围空间存在着一种叫磁场的物质，磁体间的相互作用就是以磁场作为媒介的，磁场的一个最基本的特性就是对位于磁场中的磁体或运动电荷（电流）有磁场力的作用。

    6、磁力线：在磁场中的任何一点，悬挂条形铁的北极（N极）所指的方向，就是那一点的磁场方向。在磁场中，我们可以画出一些直线或曲线，使线上的任何一点的切线方向都跟该点的磁场方向一致，这样一些线就叫做磁力线。

    永磁体外部的磁力线总是从磁体的北极出来，展伸到磁体的南极进去，因为在磁场里的任一点处，磁场只有一个方向，所以磁力线永不相交，同时通过一点只能而且总能作出一根磁力线。磁力线与电力线一样，实际上是不存在的,它只是人们假想出来的线条，以使对磁场的描述比较形象化。

7 磁感应强度：

    通电导体在磁场中受到磁场力的作用，1米长的导线，通以1安培的电流，如果受到的磁场作用力为1牛顿，那么该处的磁感应强度定为1特斯拉。

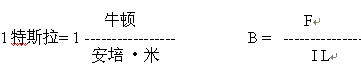
    一般永磁铁附近的磁感应强度约为0.4-0.7特斯拉，在电机和变压器的铁心中，磁感应强度可达0.8-1.4特斯拉，通过超导材料的强电流所产生磁场的磁感应可达1000特斯拉，而地面附近地磁场的磁感应强度B大约只有0.5×0.5×10^-4特斯拉。

    我们可以用磁力线的疏密来形象地表示磁场中各处磁感应强度B的大小。通过磁场中某点处，与磁感应强度方向垂直的单位面积的磁力线数目与该处的磁感应强度B的大小成正比。这样，磁感应强度B大的地方，磁力钱就比较密集，在磁感强度B小的地方，磁力线就比较稀疏。

8 匀强磁场

    在磁场里，不同的地方磁感应强度的大小和方是不同的。在磁场的某一区域里，如果各点的磁感应的大小和方向都相同，这个区域里的磁场就叫做匀强磁场里。

9 磁通量：

    在匀强磁场中的磁力线，是一组疏密均匀方向一致的平行线，垂直穿过磁场中的某一面积的磁力线的多少叫做穿过这个面积的磁通量，用Φ表示。
B的单位为特斯拉，S的单位为米²，这时Φ的单位叫韦伯，代号：Wb。
1韦伯 = 1特斯拉 * 1 米²

    磁场是由电流（电荷运动）产生的，对于“无限长”载流直导线周围产生的磁场，其磁感应强度：

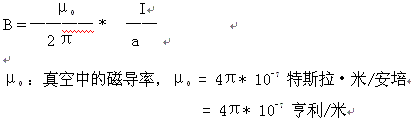
二、磁介质中的磁场

1 磁介质 磁导率

    放在磁场中的磁介质也要和磁场发生相互作用，彼此影响，这样，使介质处于一种特殊的磁化状态中，这个过程称为介质的磁化。处于磁化状态的磁介质也产生一个附加磁场，使磁介质中的磁场不同于真空中时的磁场。

    设某一电流分布在真空中产生的磁感应强度为Bo ，那末在同一电流分布下，磁场中放进了某种磁介质后，磁场和磁介质间相互.响的结果，使磁介质在磁场作用下产生附加磁感应强度B'，这时磁场中任一点的磁感应强度B等于Bo和B'的矢量和,即

B= Bo+B'

在无限长螺旋管中，电流在管内产生的磁场看作均匀的，其磁感应强度为
Bo=μ0 n I

如果在管内充满某种均匀磁介质，则由于磁介质被磁化后产生了附加磁感应强度B'，使管内磁介质中的磁感应强度为B，

2 顺磁质的磁化

    顺磁质在外磁场Bo的作用下，分子磁矩Pm的大小不改变，但附加磁矩△Pm较之Pm为很小，可以略去。此时外磁场Bo是使Pm绕磁场方向作进动的，可是，由于分子之间的相互作用(指分子之间的相互碰撞)使分子磁矩Pm改变方向，按玻耳兹曼能量分布律，Pm沿磁场方向取向时的几率最大，亦即Pm的方向有与Bo保持一致的趋势，当然，由于分子的热运动，分子磁矩的取向是不可能完全一致的。但是，也正是由于分子的热运动，在给定温度下，分子磁矩Pm与磁场方向间的角度才能按一定的统计规律分布，并使其中Pm方向愈靠拢磁场方向的分子也愈多，所以在外磁场中，分子磁矩的排列较没有外磁场时为整齐。磁场愈强，温度愈低，排列也愈整齐。这样，顺磁质物体在外磁场作用下，如果在磁体内任取一体积元△V，这体积元内各分子磁矩的矢量和ΣPm将有一定的量值。单位体积内的分子磁矩称为磁化强度，用M表示：

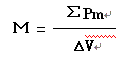
磁化强度是表征磁介质磁化程度亦即所处磁化状态的物理量。M的单位是安培/米。

    M的方向与外磁场Bo的方向一致，顺磁质经磁化后所产生的附加磁场B'的方向也与Bo的方向相同。这是顺磁性的重要表现。

3 抗磁质的磁化：

    抗磁质在外磁场中的磁化作用，完全决定于抗磁质中分子在有外磁场Bo时所产生的附加磁矩△Pm，△Pm的方向与Bo的方向相反，大小与Bo成正比。磁化强度为

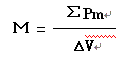
    M的方向与外磁场Bo的方向相反，经磁化后的抗磁质所产生的在抗磁质内的附加磁场B'的方向也与Bo的方向相反。这是抗磁性的重要表现。一个磁介质的磁化情况，可以用磁化强度M来描述,也可以用分子电流来反映。根据磁化强度的定义,很容易找出磁化强度与分子电流之间的关系。

    设有"无限长"的载流直螺线管,管内充满均匀磁介质，电流在螺线管内产生匀强磁场，在外磁场中，磁介质中分子电流平面将趋向于与磁场的方向垂直，磁介质被均匀磁化。

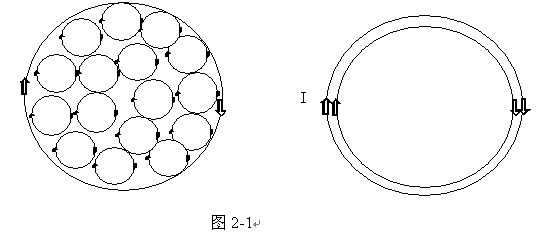
    磁介质内任一截面上分子电流排列的情况。.参看图2-1，在磁介质内部任意位置处，通过的分子电流是成对的,而且方向相反，结果相互抵消。只有在截面边缘处，分子电流未被抵消，形成与截面边缘重合的圆电流，对磁介质的整体来说，未被抵消的分子电流是沿着柱面流动的，称为安培表面电流。对顺磁性物质，安培表面电流和螺线管上导线中的电流I方向相同，对抗磁性物质,则两者方向相反。图2-1所示是顺磁质的情况.

4 磁场强度：

    Ｈ矢量的环流只和传导电流I连着，而在形式上与磁介质的磁性无关。当传导电流I给定以后，不论磁场中放进什么样的磁介质(或者同一块磁介质在不同的地方)时，虽然在不同情况下同一点的Ｈ矢量有所不同，但Ｈ矢量的环流只和传导电流连系着。因此，引入磁场强度Ｈ这个物理量以后，能够使我们比较方便地处理有磁介质时的磁场问题。

    在国际单位制中，Ｈ的单位是安培/米

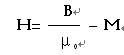
    上 式是磁场强度的定义式，不论磁介质是否均匀，而且对铁磁性物质,也用此式定义磁介质中的Ｈ矢量。或者说，用此定义式来表示磁介质中任一点处磁感应强度B、磁场强度Ｈ和磁化强度Ｍ之间的普遍关系,并写成

    通常把磁介质中任一点处Ｍ矢量和Ｈ矢量之间的关系用另一个式子表示,这就是

    对于各向同性的磁介质,在磁介质中任一点,磁化强度Ｍ和磁场强度Ｈ成正比,也就是说式中比例系数Xm是恒量,称为介磁质的磁化率，它的量值只与磁介质的性质有关。因为Ｍ和Ｈ所用的单位相同,所以磁化率Xm是一个没有单位的纯数。

这是把磁介质中任一点处B矢量和Ｈ矢量直连系起来的关系式，
令μr =1+Xm
μr就是该磁介质的相对磁导率。
B=μ0μr Ｈ =μ Ｈ

    对于各向同性的磁介质， Xm例是恒量，μr也是恒量，且都是纯数，μr = 1 +Xm，或Xm =μr-1，.磁介质的磁化率Xm、相对磁导率μr、磁导率μ都是描述磁介质磁化特性的物理量,只要知道三个量:中的任一个量，该介质的磁性就完全清楚了。

    所有顺磁性、抗磁性材料的磁化率的值都很小，其相对磁导率几乎等于1，说明了它们对电流的磁场只产生微弱的影响。

三、铁磁质

１ 磁滞回线

    对于铁磁质来说,铁磁质中任一点处的B、Ｍ、Ｈ 三矢量之的普遍关系,仍采用上式。事实上,铁磁质中B 与Ｈ及Ｍ与Ｈ之间，并没有线性的正比关系。虽然在形式上仍引用式 2-14)和式(12-13〉,但式中铁磁质的磁导率μ、相对磁导率μr和磁化率Xm并不是恒量。由于铁磁质有磁滞现象，B 和Ｈ之间不具有简单的线性关系。

    如果在电流的磁场中，放入铁磁性物质，那末，磁场将显著地增强,这时在铁磁质中的磁感应强度B 比单纯由电流产生的Bo增大百倍、甚至千倍以上。不仅如此，铁磁质还具有一些特殊的性质：(1)它们的B和Ｈ不是简单的正比关系，而是比较复杂的函数关系。换句话说，铁磁质的磁导率μ(以及磁化率Xm)不是恒量，而是随磁场强度Ｈ变化着的。〈2)在外磁场停止作用后，铁磁质仍能保留部分磁性。(3)它们各具有一临界温度称为居里点，在这温度，它们的磁性发生突变，当温度在居里点以上时，它们的磁导率(或磁化率)和磁场强度Ｈ无关，这时铁磁质转化为顺磁质。铁的居里点是1040K，镍是631K，钴是1388K。

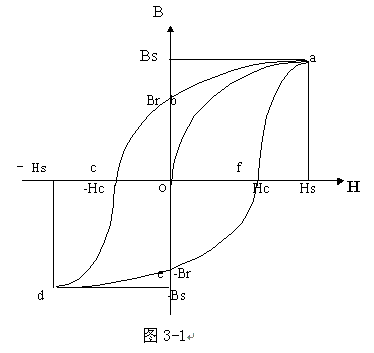
    从B - H曲线图上可以看到，在开始时磁感应强度B 值随磁场强度Ｈ的增加而急速地增加，当Ｈ达到一定的强度，B的值不再随H的增强而增加，这时磁化己达到饱和。磁感应强度的饱和值用Bs表示。如果在达到饱和状态之后，使H减小，这时B的值也要减小，但不沿原来的曲线下降，而是沿着另一条曲线下降，对应的B值比原先的值为大，说明铁磁质磁化过程是不可逆的过程。.当H=0时，磁感应强度并不等于零，而保留一定的大小Br ,如图3-1的线段Ob，这就是铁磁质的剩磁现象。要使B继续减小,必须在绕组中通入反向电流，加上反方向的磁场。当H等于某一定值Hc时,如图中线段Oc，B才等于零，这个Hc值，称为矫顽力。矫顽力Hc的大小反映了铁磁材料保存剩磁状态的能力。

    如果再增强反方向的磁场，又可达到反方向的饱和状态。以后再逐渐减小反方向的磁场至e点，这时改变绕组中的电流方向，又引入正向磁场，,则形成图所示的闭合回线。从图3-1可以看出，磁感应强度B值的变化总是落后于磁场强度H的变化,这种现象称为磁滞，是铁磁质的重要特性之一。.所以，上述闭合曲线称为磁滞回钱。研究铁磁质的磁性就必须知道它的磁滞回线，各铁磁质有不同的磁滞回线，主要区别在于矫顽力的大小。

2 磁畴：

    铁磁性不能用一般顺磁质的磁化理论来解释。因为铁磁性元素的单个原子并不具有任何特殊磁性，例如：铁原子与铬原子的结构大致相同，但铁是典型的铁磁质，而铬是普通的顺磁质，甚至还可用非铁磁性物质来制成铁磁性的合金。另一方面还应注意到铁磁质总是固相的。这些事实说明了铁磁性是一种与固体的结构状态有关的性质。

    在铁磁质中,相邻铁原子间存在着非常强的交换耦合作用，这个相互作用促使相邻原子的磁矩平行排列起来，形成一个自发磁化达到饱和状态的区域，自发磁化只发生在微小区域内，这些区域称为磁畴。在没有外磁场作用时，在每个磁畴中，原子的分子磁矩均取向同一方位，但对不同的磁畴，其分子磁矩的取向各不相同。磁畴的这种排列方式，使磁体能处于能量最小的稳定状态。.因此，对整个磁体来说，任何宏观区域的平均磁矩为零，物体不显示磁性。

    在外磁场作用下，磁矩与外磁场同方向排列时的磁能将低于磁矩与外磁场反向排列时的磁能，结果是自发磁化磁矩和外磁场成小角度的磁畴处于有利地位，磁畴体积逐渐扩大，而自发磁化磁矩与外磁场成较大角度的磁畴体积逐渐缩小。随着外磁场的不断增强，取向与外磁场成较大角度的磁畴全部消失，留存的磁畴将向外磁场的方向旋转，以后再继续增加磁场，使所有磁畴沿外磁场方整齐排列，这时磁化达到饱和。因为磁畴和外磁场方向成较小角度的磁畴体积扩张并不是逐渐进行的，而是在磁场达到一定强度H时，突然地进行的，这就反映了过程的不可逆，表现出磁滞现象。同时,各个磁畴还受到阻碍它们转向的摩擦阻力，因而在外磁场停止作用后，磁畴的某种排列被保留下来，使磁体留有部分磁性,表现为剩磁现象。

3 软磁材料

    铁磁性材料在工程技术上应用很广，不同的磁性材料导磁性能各不相同，一种磁性材料是否适用于某种用途，工程上常常是依据它的磁滞回线来决定。根据磁滞回线的不同,可以将铁磁性材料区分为软磁材料和硬磁材料。

    软磁材料的特点：磁导率大，矫顽力小( Hc〈 10²安/米),磁滞损耗低，它的磁滞回线成细长条形状。这种材料容易磁化，也容易退磁，适用于交变磁场,可用来制造变压器、继电器、电磁铁、电机以及各种高频电磁元件铁芯。

    4 硬磁材料

    硬磁材料的特点是：:矫顽力大(Hc>10²安培/米)，剩磁Br也大。这种材抖的磁滞回线所包围的面积肥大，磁滞特性显著，因此，硬磁材料充磁后，仍能保留很强的剩磁，并且这种剩磁不易消除，这种硬磁材料适合于制成永久磁铁。例如，磁电式电表、永磁扬声器、耳机、小型直流电机以及雷达中的磁控管等用的永久磁铁，都是由硬磁材料做成的。

四、磁路定律

    在截面积为S、长为L的、磁导率为μ的铁环上，绕以紧密的线圈N匝，设线圈中通过的电流为I，根据安培环路定律，
∮H d L =ΣI
应用到环中任一磁感应线，得到 H L=N I，通过任一截面的磁通量为 Φ=BS=μHS

因此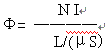


NI 称为磁通势εm，L /(μS)称为磁阻Rm，则磁通与电流相当，可记为

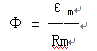
磁阻Rm与磁导率μ是反比关系，磁导率越大，则磁阻越小，磁通量亦越大。

五、磁场的能量

    对一个具有自感的简单电路来说，当这个电路中通有稳定电流时，导线周围建立一定能量分布的磁场，这时维持电路中稳定电流的电源所供给的能量将全部转化为电路中放出的焦耳-楞次热。但在电路中电流由零增加到稳定的过程中，即在电流变化的过程中，电路中出现自感电动势，这时电源所供给的能量，除一部分转化为焦耳-楞次热外，另有一部分要克服自感电动势作功，这后一部分就在建立磁场过程中转化为磁场的能量。另一方面，当电路中的电流衰减时，自感电动势的作用是维持电路中的暂时电流，自感电动势的方向和电流方向相同，因此讨论时,常说这时的自感电动势在电路中作正功，向电路供应能量，其实这能量就是由磁场能量释放出来的。

    设有自感为L的线圈，在线圈中电流由零增加到稳定值I的过程中，线圈中产生自感电动势

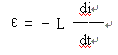
i是线圈中某瞬时的电流，在dt时间内，电源电动势反抗自感电动势而作功
dA= -εi   dt = Lidi
根据功能原理,这功dA等于线圈中磁场能量Wm的增量dW即dWm=dA=Lidi
当电流从零增加到稳定值I，对上式积分，得

在L不变的情况下,得

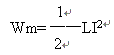
式中L的单位用亨利，,I的单位用安培,则Wm的单位为焦耳。

    上式是用线圈的自感及其中电流表示的磁能，经过变换，磁能也可用描述磁场本身的量B、H来表示。为了简单起见，考虑一个很长的直螺线管，管内充满磁导率为μ的均匀磁介质。管中磁场近似看作均匀，而且把磁场看作全部集中在管内，设通过螺线管的电流为I，则螺线管内的磁感强度B= μnI，它的自感系数L=μn²V，式中n为螺线管单位长度的匝数，V为螺线管内磁场空间的体积，把L及I0=B/（μn）代入式(5-1),得到磁能的另一表示式

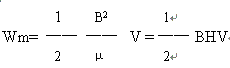
而磁场能量密度是:

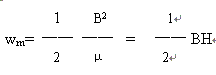
    上述磁场能密度的公式虽然是从螺线管中均匀磁场的特例中导出的，但它是适用于各种类型磁场的普遍公式。公式说明，在任何磁场中，某一点的磁场能量密度，只与该点的磁感应强度B和介质的性质有关，也说明了磁能是定域在磁场中的这个客观事实。

六、磁引力与磁引力能

    设面积为Am的一块磁体，与面积为A的一块衔铁距离为Lg，若衔铁与磁体之间的磁通密度和磁场分别为Bg与Hg，则气隙内的能量密度为BgHg/2，磁体对衔铁有一吸引力F，如果外力使衔铁与磁体的距离增加d Lg，则这个外力必须反抗吸引力F而作功dW=F* Lg，其结果是使气隙能量增加dE，衔铁距离增加d Lg后，相应的气隙体积增加为A g*d Lg，所以气隙能量增加为

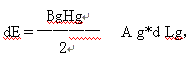
这个能量增加与外力反抗吸引力F所作的功dW相等，

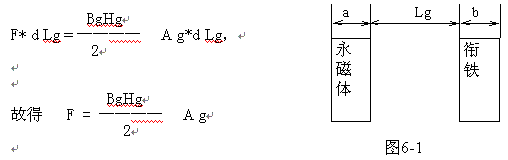
上式说明，吸引力与气隙的面积A g、气隙的磁场Hg、磁通密度Bg成正比，与衔铁宽度b无关（图6-1），增加Hg需采用矫顽力高的材料。
磁力公式的分析：
永磁体原来的气隙能量就是等于永磁体本体的能量

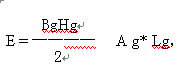
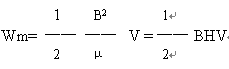
    如果衔铁与永磁体相距很远，则上述二式相等。在永磁体能够作用到的距离中，若衔铁与永磁体的距离发生了变化，则两者之间气隙磁能的增加量就是外力必须反抗磁引力所作的功，气隙磁能的减少量就是磁引力可对外作的功，而同时气隙磁能的增加量或减少量亦就是衔铁磁能的减少量或增加量，即气隙磁能与衔铁磁能是一个能量守恒关系。衔铁为了存储气隙磁能的减少量，就必须有一定的体积V，因为

    如果，衔铁的特性与体积能够全部接受永磁体对其的磁化能，上述推导的磁力公式就能成立，因为要有一定的体积，所以衔铁要有一定的厚度。如果一定的体积量已能够全部接受永磁体对其的磁化能，再增加体积就没有意义了。

    永磁体磁化衔铁的状况是这样的情况：如图(6-2)所示

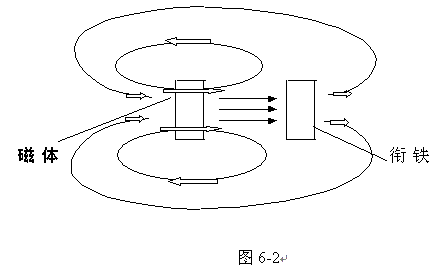
    在一定的距离中，永磁体的磁力线一部分自已闭合循环，一部分感应衔铁，被感应出来的衔铁另一端的磁力线回到永磁体的另一端，符合磁力线永不相交但又是闭合的规律。

    衔铁在磁场中受到磁化后，其前后界面的磁通量是相同的。永磁体对衔铁进行磁化，若衔铁前界面受到了N极的磁化，则衔铁的前界面被磁化成S极，有X根磁力线，则衔铁的后界面一定会产生相同数量的磁力线为N极，即前后界面的磁通总量是相等的，若前后界面的面积相等，则磁场密度也相等，这亦是铁磁性材料被磁化的基本规律。

    相对于某一固定永磁体，若要分衔铁前后界面的气隙能量的话，衔铁前界面气隙能量的减少量亦就量衔铁后界面的气隙能量的增加量，衔铁在磁场中的任一位置，衔铁前后界面的气隙能量的和就是等到于某一固定永磁体本身所具有的磁力能。

    在实际过程中，永磁体与衔铁的力的关系是不会如公式所述的那样简单，它与很多因素有关，所以对一具体的永磁体与衔铁的力与距离的关系是通过试验作出来的，如图6-3所示：

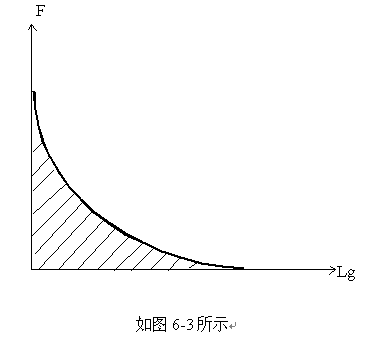
阴影部分才是真正的磁场力可作的功。它当然比永磁体本身所具备的磁能小。

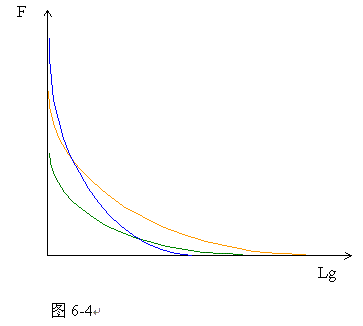
    重量相同形状不同的磁体亦对应着不同的F-Lg曲线，棒形磁体的牵引力随Lg的变化较慢，虽然牵引力较小,但作用范围较大(Lg较大);而贝字型磁路的牵引力则随Lg变化很陡，就是说，当Lg很小时,牵引力可以很大。每种形式的磁路虽然各自都有自己的F-Lg曲线，如图6-4示，但在同一形式的磁路中，各部件按同一比例尺寸放大以后，其F-Lg曲线的形状则不变,只不过坐标分度增大而已。

七、动态磁路的设计

    磁场发生变化的磁路称为动态磁路,气隙磁场的变化可以是由于气隙尺寸距离的变化引起的,也可以是由于其他干扰磁场引起的,或者是这两个因素同时引起的。

    1 动态磁路一：

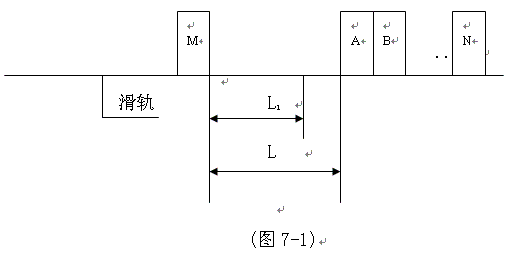
边界条件：
1)    M：已磁化的永磁体，磁极在左右两端。
2)    A、B···N：软磁性材料，左右间尽寸宽度为b（图未标） 。
3)    A、B···N、M ：均为刚性材质。
4)     滑轨：与磁性不会产生作用力的材料，水平按装。当磁性材料在滑轨上滑动时无摩擦力产生。
5)    对于某一固定永磁体，对有限个软磁体A-N与其逐个串联接触，永磁体M总磁通量不发生变化，则对应的磁引力能亦不发生变化。

    永磁体M左右两侧装有固定装置，即M不能向左右侧运动，当A左端与M 右端相距L距离时，相互之间没有产生作用力，当A沿着滑轨向左滑动到与M 相距为L1距离时，M 与A之间开始产生磁引力Fa，此时M 对A有一磁引力能Wa，永磁体M 的磁通量分为两部分，一部分通过软磁体A，称为有用磁通量Φu，另一部分不经过A，而是永磁体M 本身走回路，称为漏去磁通量ΦL。在引力场的作用下，A将沿着滑轨向M 移动，在滑动过程中，磁引力Fa反抗外力而作功，A可通过某一装置将磁引力所作的功对外输出。随着磁引力反抗外力作功，A越来越靠近M ，则磁引力亦在增加，经过A的有用磁通量亦增加。当A与M 完全吸在一起后, 气隙能量为零，M 的磁通量全部经过A。在理想转化过程中，永磁体M 磁能所作的功Wa 完全对外输出。

    在A向M滑动过程中，其有用磁通量的逐步增加就意味着M与A之间的气隙能量在逐步减少，最终为零。

    当A与M 完全吸在一起后，因为磁阻Rm与磁导率μ是反比关系，磁导率越大，则磁阻越小，磁通量亦越大。而A的导磁率μ>>空间导磁率μ0，所以，可认为M 右端的磁力线完全经过A的右端向外发出。当B沿滑轨向左滑至距M 为L2时(图未标出)，则B就开始进入一个引力场。即M 对B也产生了一个磁引力能Wb，与A不同的是M 的磁力线是经过A而对B起了作用。在引力场的作用下，B将沿着滑轨向M 移动，在滑动过程中，B可通过某一装置将磁引力所作的功对外输出。在理想状态下，Wa=Wb。此时图示系统对外输出的能量为W=Wa+Wb=2Wa，依此类推， 上述过程进行了n次后，则对外输出能量为W=n*Wa，其状态由(图7-1)到了(图7-2)。

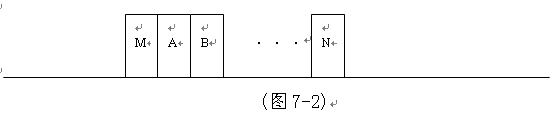
    现将力作用于A，使A向右滑动，在滑动过程中，A右端的软磁性材料被带着一起滑动，而A-N整体必须克服M 对其产生的磁引力能Wa， 而这个Wa必须由外系统输入。在滑动过程中，永磁体M 的磁通量亦分为两部分，一部分通过软磁体A-N，称为有用磁通量Φu，另一部分不经过A-N，而是永磁体M 本身走回路，称为漏去磁通量ΦL。在外力场的作用下，A-N将沿着滑轨向右滑动，在滑动过程中，外力要反抗磁引力而作功，随着A-N的右移，则磁引力亦在减少，经过A-N的有用磁通量亦减少。当A与M 相距L1时，磁引力也就消失。若A由L1距离继续右移至L距离，这个过程则无需能量交换，整个过程又回到图7-1状态。

    在A向右滑动过程中，其有用磁通量的逐步减少就意味着M与A-N之间的气隙能量在逐步增加，最终为M本身具有的磁能Wa。

    上述过程进行了一个循环后，图示系统对外输出能量n*Wa，外系统对图示系统输入能量Wa，则有能量差：(n-1)*Wa，这个(n-1)*Wa的能量是图示系统对外系统输出的能量，而图示系统对外输出了(n-1)*Wa的能量后图示系统本身的能量(磁引力能量)并没有减少，即外系统无偿地得到了能量(n-1)*Wa。这里的关键是：A,B···N体相对于M 而言分别均有一个磁引力的势能Wa, 通过一定的装置将其能量分别输出，总和为n*Wa,而这些物体整体克服M 的磁引力势能时,所需输入能量为Wa。如果上述循环连续进行，则就可连续得到能量(n-1)*Wa，即这个图示系统就可以源源不断的输出能量，而其本身又没有消耗新的能量，那就可以说：这个图示系统是一个“永动机”的动力源。当然，在实际滑动过程中以及通过一定的装置将能量转化过程中，这个图示系统中的能量总是有一定的损耗的， 但上述原理总是存在的(上述过程各种能量转换的具体形式是可以不同的)，只要尽量减少各种损耗，对各个能量传递、转换方面进行完善，那么图示系统的输出能量(n-1)*Wa减去损耗能量Ws后的部分就可以被人们来利用了。

备注：
根据磁路定律

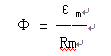
    对于某一固定永磁体，磁通势εm不变，对于有限个软磁体A-N与其逐个串联接触，其磁阻Rm将要逐渐增加，所以永磁体M 总磁通量逐渐减少，其对应的磁引力能亦逐渐减少，如果软磁体宽度b尽量短（磁引力与宽度b无关），截面积为S足够大，磁通率μ足够大（工业纯铁其相对磁导率μr =5000，超坡莫合金μr = 66000），对有限个软磁体A-N与其逐个串联接触，磁引力能亦将逐渐缓慢地减少。即在图7-1到图7-2中，随着软磁体逐个与永磁体M 串联接触，其磁引力能输出亦将逐渐缓慢地减少，其总的磁引力能输出比上述的理想状态(n-1)*Wa要小。不论如何，上述总的工作趋势是不变的。

2 动态磁路二：

    边界条件与动态磁路一相同。起始状态从图7-2开始

    现将力作用于N，使N向右滑动，在滑动过程中，必须克服磁引力FN ，当右移到足够远FN =0时，外界使其右移所输入的功为WN ，N在右移过程中，受到的磁引力根源在于永磁体M ，而磁力线是通过软磁体N-1右端发出对N产生了磁引力FN ，原因与前述相同，在理想状态，M的磁引力能所作的功W与输入的功WN 相同，W = WN 。
再将软磁体N-1右移，右移到足够远时FN-1 =0，外界使其右移所输入的功为WN-1，在理想状态，WN-1 = WN = W 。依次类推，将软磁体逐个右移，每次所作的功与磁引力能所作的功W相等。当A亦右移至磁引力FA =0时，则外界输入的总功为W=n*Wa，其状态由(图7-2)到了(图7-1)。

    现将软磁体A-N作为一个整体左移，当移至L1时，M 与A－N之间开始产生磁引力Fa，此时M 对A－N有一引力能Wa，在引力场的作用下， A－N将沿着滑轨向M 移动，在滑动过程中，吸引力F反抗外力而作功，A－N可通过某一装置将磁引力所作的功对外输出。随着磁引力反抗外力作功，A－N越来越靠近M ，则磁引力亦在增加，经过A－N的有用磁通量亦增加。当A－N与M 完全吸在一起后, 气隙能量为零，M 的磁通量全部经过A－Ｎ。在理想转化过程中，永磁体M 磁能所作的功Wa 完全对外输出。其状态由(图7-1)回到了(图7-2)。

    上述过程进行了一个循环后，图示系统对外输出能量Wa，外系统对图示系统输入能量n*Wa，则有能量差：(n-1)*Wa，这个(n-1)*Wa的能量是外系统对图示系统输入的能量，而外系统对图示系统输入了(n-1)*Wa的能量后，图示系统本身的能量(磁引力能量)并没有增加，图示系统与外系统亦没有其它形式的能量或热量产生，即图示系统无偿地得到了能量(n-1)*Wa，并且将其消失于无形之中，如果上述循环连续进行，则就可连续将能量(n-1)*Wa消失于无形之中，那么，这个图示系统就变成了“永动机”的对立面，暂且叫做“不动机”。

    备注

    根据动态磁路一中的备注，从图二到图一的过程中，需克服的磁引力能将逐渐增大，最大为Wa，而A-N作为一个整体左移时，磁引力能的输出最大，因此，总的将能量消失于无形之中的数量比理想状态(n-1)*Wa来的小。

八、总结

    若动态磁路一、动态磁路二成立的话，那么就会有这样的结论：引力产生了运动，运动产生了“永动机”， 运动亦产生了“不动机”。

    从更大的范围而言，就可以这样的结论：引力会产生运动，运动会产生“永动机”， 运动亦会产生“不动机”。

    现在的观点认为：能够自行产生能量的永动机是不存在的，能量是只能从一种形式转换到另一种形式。那么，动态磁路一、动态磁路二也许就打破了这种观点。

    我非常清楚稿件所述的目标与当今科学共识之间的矛盾,但是稿件所述的动态磁路一、动态磁路二中的各个过程并没有违反当今的科学规律，也许上述图示系统所产出或消失的能量只能在实验室中被证明，要应用于人类的各项活动中还有很长的路，但这是人类对能量认识的进步，是探索能量从无到有和从有到无的开始。通过人类积极探索能量的特点，使人类在将来的活动中能更好地与自然互相协调，共同发展。

    若本稿有疑点之处，请详尽指出，以利本人的提高。

上海闸北发电厂 生产技术计划科 沈建平
地址：军工路4000号 邮编：200438 电话：021-65057001-2129
wying104@sohu.com
2001/11/15

     版权所有，保留一切权力，未经授权使用将追究法律责任 版权说明  © Copyright  Authors
物理科学探疑

返回首页