物理科学探疑-网友天空-系统观点-陈寿元-感应引力的天文观测证据
![]()
感应引力的天文观测证据
陈寿元
(山东师范大学,教工高层公寓10-1803室, 济南,250014
Tel: 0531-6189538,E-mail:chensy@beelink.com)
摘要 物体运动状态的改变将产生感应引力的理论概念,得到日食期间的重力异常低谷现象的支持。该重力低谷与月球插入或离开日-地形成的锥形区有关,对应量与月球使日-地系统运动状态的变化量有关。
关键词 感应引力;日食;引力
0引言
众所周知,法拉第的电磁感应实验:磁铁插入或离开闭合线圈时,有感应电流或电压产生。实验如图1(A)、(B)所示:
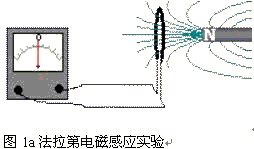
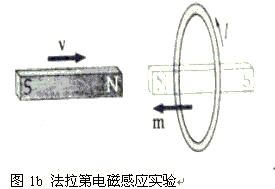
法拉第根据实验事实综合出电磁感应定律:“当运动电荷的磁场发生变化时,要产生感应电场”。该实验成为电磁学发展的基石。
牛顿第二定律:外力是物体的运动状态发生变化时的源泉;相对静止观点:物体的运动状态发生改变时,对外界要产生感应(影响)或称为感应引力[1]。我们如何寻找感应引力:万有引力不是靠实验综合出来,而是牛顿根据天文现象综合出来。雷同的思路,由于感应引力也很弱,靠实验不易成功,寻找合适的天文现象,从中综合出的感应引力的具体形式。近几年的天文观测发现,由日食期间,重力异常减小观测事实,分析当物体运动状态发生变化时,对外界产生的感应引力的具体形式。
物理学家Alis于1954、1959年两次实验,发觉日全食前后地球重力会有异常变化现象。
1995年日全食期间,印度科学家首次观测到“食甚”前约一个小时的12个微加重力低谷。1997年3月9日,中国科学家在漠河的日全食观测中,测量到有两个异常的重力场低谷,这两个低于理论值的重力谷对称地发生在日食“初亏”和“复圆”之际,有4-5个微加的“重力双谷”。2000年在澳洲的日食观测中、2001年6月21日非洲日全食,都得到类似的结果。这种重力异常减小现象,引起国际物理学界的关注,迄今为止难以解释[2,3]。
1日食期间重力异常低谷现象
1、 1日食现象
月球在绕地球运行的过程中,有时会走到太阳和地球的中间,月球的影子落在地球的表面上,在影子里的观测者就会看到太阳被月球遮蔽的现象,叫做日食。 日食分日全食、日偏食与日环食三种。全盘和环食的过程分初亏、食既、食甚、生光、复国等5种食象,偏食只有初亏、食甚与复圆3种食象。对于日全食,从食既到生光只有三、四分钟,有时不到一分钟。月球在地面上形成的本影区,在地面的西边缘开始形成,自西向东扫过的地带称为全食带,在东边缘结束。如图2所示。
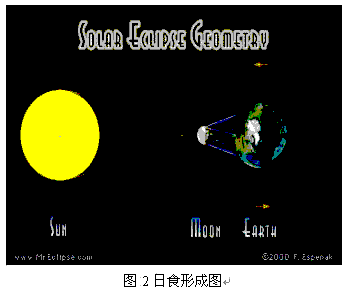
1、2 1995年重力异常低谷现象
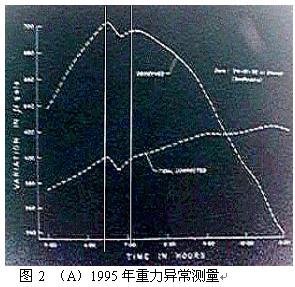
1995年10月24,日食首先在伊朗形成,在太平洋结束。观测者在印度的Dhoraji镇(22o44′,70o27′),测量到日全食前约1小时的重力异常[1]。如图2所示[1]
重力低谷对应的时间(地方时)上午6:30到7:15,日食在1995年10月24日新德里时间的上午7:22在伊朗最早形成,自西向东移动,很快进入印度(即观测点附近),4个小时后在太平洋结束[1]。该观测点仅看到日偏食,偏食食分80%。接近全食带的起点,远离全食带的终点。
1、3 1997年重力异常双谷
1997年3月9日的这次全食,全食带从亚洲北部开始,在北冰洋结束。漠河在全食带内,我国科学家在漠河首次发现日食期间有两个异常的重力场低谷,这两个重力谷对称地发生在日食“初亏”和“复圆”之际, 4-7个微加的“重力双谷”。如图3所示[2]:
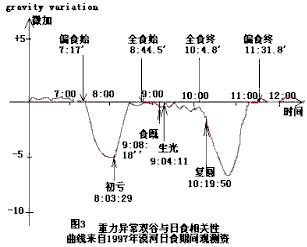
在图3看出,1997年3月9号,漠河观测到的日食时间为:初亏时间8:03:29;食既9:08:18;生光9:04:11;复圆:10:19:50。曲线为日食发生时测量到的重力变化量。很明显重力减小双谷与漠河该点的日食[2]没有关联一致性。
1997年天文年历给出的预报,97年3月8、9日的日食[3]:
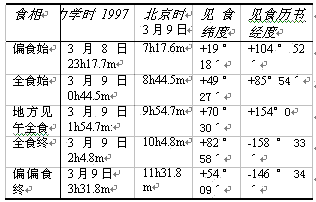
重力的第一个低谷在偏食始到全食始,第二个低谷在全食终到偏食终。对应的相关性有交好的吻合。
2重力异常与天体几何位置
月球在绕地球运行的过程中,有时会走到太阳和地球的中间,月球的影子落在地球的表面上,在影子里的观测者就会看到太阳被月球遮蔽的现象,叫做日食。
日食开始时,月球圆轮与地球圆面西边缘相切于H1点,地表上点在当地日出时见初亏,这也是地球上最先看到初亏的地点。故在日食图上标为偏食始。月轮继续向东移动,在地面上开始形成本影时,即日全食开始。月球向东移动,本影消失,即全食终,到偏食终。太阳、地球、月亮三者的空间关系如图4所示:
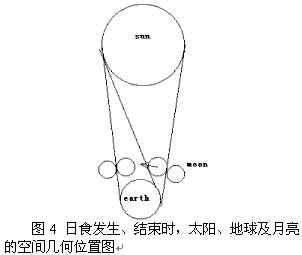
用太阳球面与地球公切面,形成一个锥形体,太阳一端粗,地球一端细。月球围绕地球做公转运动,进入或离开锥形面。当要进入时,正好与锥形面外切,在地面的西边缘,形成日偏食,即偏食始。全日食在西边缘最早形成时,月球与圆锥面内切。这对应偏食始到全食始。表现全日食过程有全食带如下图所示:
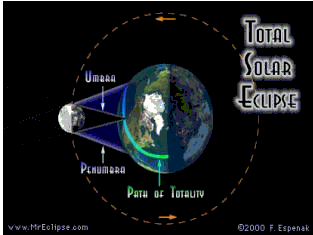
1995年印度测量到的重力场低谷与其对应,1997年测量到的重力双谷,时间上早的那一个低谷也是与偏食始到全食始对应。后一个重力低谷与全食终到偏食终对应。
3模型分析
众所周知,法拉第由磁铁插入或离开闭合线圈时,有感应电流或电压产生的实验事实,综合出电磁感应定律:“当运动电荷的磁场发生变化时,要产生感应电场”。牛顿第二定律:外力是物体的运动状态发生变化时源泉;现在由日食期间,当月球插入或离开日-地形成的锥形区时,有重力减小的观测事实,探讨当物体运动状态发生变化时,对外界产生的感应。
为了讨论方便,设计一个简单模型,一个质量均匀无极性的小球,两个结构对称,并且平行的物体构成的均匀引力体系,体系的动量只有小球进入或离开时,才会变化.①小球从引力体系一端进入,引发的感应引力的方向,与从同一端离开,其感应引力方向相反;②小球从引力体系一端插入,与从引力体系另一端离开,其感应引力方向相同,这与磁铁的N极从线圈的一端插入,感应的电场方向;与N极从线圈的另一端离开时相同.
由简单模型得:感应引力f=–k(dp/dt);
小球进入体系的体积部分:V=(1/3)·πρh2(3R-h);使体系的动量增加量:P=(1/3)
πρh2(3R–h)υ;感应引力:f=–k(dp/dt)=–kπρh(2R–h)υ2;式中;![]()
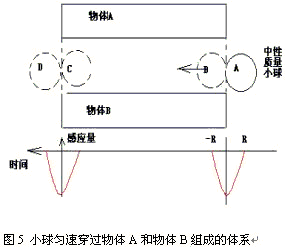
讨论:①当h=0, 小球处于外切;相当于地面上最西端,最早观测到日食发生,日偏食开始:f=–k(dp/dt)=0;②当h=R, 小球一半已进入体系,感应量最大:f=–k(dp/dh)(dh/dt)= –kπρυ2R2;为负的最大值;相当于日食发生时,半个太阳被当住情形;③当h=2R,小球正好全进入体系,处于内切f=–k(dp/dt)=0;相当于日食发生时,日偏食结束,日全食开始.④当小球全部进入体系,继续匀速前进,相当于日食发生时,从日全食开始至日全食全过程结束.体系的动量没有变化,感应引力为零.⑤当小球从体系的另一端离开,分析类同,如图4所示.该简单模型分析所得图形,与月亮插入和离开太阳和地球形成的锥形区时,重力减小.月亮全部进入太阳和地球形成的锥形区后,引力恢复正常的观测结果吻合.
4讨论
从1997年的重力减小测量图,可知:①日食期间产生感应引力,其方向与地球引力相反,使地球上重力减小.②.如果太阳质量是均匀分布,日偏食开始到日全食开始,这段时间是月球插入太阳与地球之间,太阳与地球的引力体系的动量增大,产生感应引力.但是,从实测图形得出,在日偏食开始之后约13分钟,重力开始减小,它又在全食始之前约13分钟结束.在全食终到偏食终之间的感应引力也有类似问题.
原因分析,可能由于太阳温度很高,太阳质量不是均匀分布,外层是很厚的气体,发光但质量很轻,对感应引力贡献很小.质量主要集中在0.86R内.如图5所示
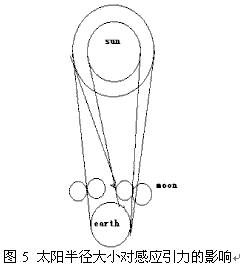
对于重力的作用也主要集中在太阳的0,86半径内。1997年3月9日的日食,偏食始到全食始是1小时27分。它对应的0、14就是12、6分。与日偏食开始之后约13分,重力开始减小正好吻合。同理可知低谷的另一个边沿早全食始约13分钟恢复正常的的原因。
1995年印度科学家仅测量到重力减小单谷如2所示,测量点位于(北纬22°44′;东经70°27′),靠近偏食始到本影形成区,所以测量到偏食形成时的感应量。由于该测量站远离偏食终点,偏食结束引起的引力变化量很微弱,测量不到是正常。
两次测量到的数值有区别:95年测量低谷的小大值约12*10-8cm/s2;97年测量重力异常双谷之间也有差异,偏食始对应的有5*10-8cm/s2,偏食终对应的约7*10-8cm/s2。可能有两方面的原因,与进入点引力场强有关,与感应量的形成点到测量点的距离有关。
致谢:本文在山东师范大学李保宏教授指导,科学院汤克云研究员的支持。
参考文献 :
[1] 陈寿元,相对静止论,山东大学学报(工学版),2002,32(4):396--400
[2]D.C Mishra, M.B.S.Rao.Temporal variations in gravity field during solar
eclipse on 24 October 1995.NASA www 网站
[3] Qian-shen Wang, Xin-she Yang. Precise measurement of gravity variations during a total
solar eclipse[J]. Physics Review 2000,D(62):41101~41103
[4]紫金山天文台,1997 天文年历,科学出版社,1997
Measurement affirm of induction gravity
Shouyuan Chen
(Shandong Normal University 250014 Jinan , P.R. China)
Abstract The gravity during a total solar eclipse weaken, we think the
phenomenon would be that when the motion of the object is changed, the inducting
gravitation can be produced.
Keywords gravitation variation; solar eclipse; induction gravity
![]() 版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
版权所有,保留一切权力,未经授权使用将追究法律责任 版权说明
© Copyright Authors
物理科学探疑